Lecture 33 - Linear data structures
Logistics
- HW6 due tonight, HW7 will be released this weekend
Learning objectives
By the end of today, you should be able to:
- Understand the LIFO (stack) and FIFO (queue) principles
- Identify when to use stacks vs. queues vs. deques
- Use Rust's
Vec,VecDequefor implementing these structures - Analyze the time complexity of operations on each structure
- Recognize real-world applications of these data structures
Motivation: Different access patterns
We've mostly used Vec<T> for resizable lists so far:
#![allow(unused)] fn main() { let mut v = vec![1, 2, 3, 4, 5]; v.push(6); // Add to end v.pop(); // Remove from end v[2]; // Access by index }
But what if we need:
- Add to one end and remove from the other? (Queue at a store)
- Only add/remove from the top? (Stack of plates)
- Efficiently add/remove from BOTH ends?
Today's question: What structures support these patterns efficiently?
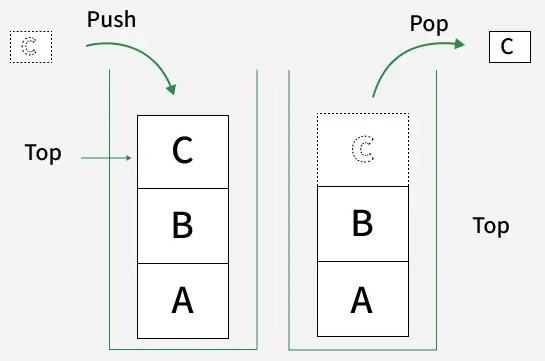
What is a stack?
Think of: A stack of plates, stack of books, stack of variables in Rust
Operations:
- Push: Add item to the top
- Pop: Remove item from the top
- Peek/Top: Look at top item without removing
Key property: LIFO - Last thing you put in is the first thing you take out
Stack memory vs stack data structure
Stack memory: Memory region where local variables live
Stack data structure: Abstract data type with LIFO behavior
- Can be implemented with any underlying storage
What they have in common: Both follow LIFO principle
- Function call stack: Last function called is first to return
- Stack data structure: Last item pushed is first to pop
Stack example: Reversing a word
fn reverse_string(s: &str) -> String { let mut stack = Vec::new(); // Push all characters onto stack for ch in s.chars() { stack.push(ch); } // Pop all characters off stack let mut result = String::new(); while let Some(ch) = stack.pop() { result.push(ch); } result } fn main() { println!("{}", reverse_string("hello")); }
Real-world stack applications
1. Function call stack:
#![allow(unused)] fn main() { fn a() { println!("A starts"); b(); println!("A ends"); } fn b() { println!("B starts"); c(); println!("B ends"); } fn c() { println!("C starts"); println!("C ends"); } // Output: // A starts // B starts // C starts // C ends // B ends // A ends }
Call stack: a() calls b() calls c() → c() finishes, b() finishes, a() finishes (LIFO!)
2. Undo/Redo:
- Each action pushed onto undo stack
- "Undo" pops from undo stack, pushes to redo stack
- "Redo" pops from redo stack, pushes to undo stack
3. Balancing parentheses:
- Push open brackets:
(,[,{ - Pop when you see close brackets:
),],} - Balanced if stack is empty at end!
Implementing a stack in Rust
Good news: Vec<T> already works perfectly as a stack
fn main() { let mut stack: Vec<i32> = Vec::new(); // Push operations stack.push(10); stack.push(20); stack.push(30); println!("Stack: {:?}", stack); // Pop operations if let Some(top) = stack.pop() { println!("Popped: {}", top); } println!("Stack: {:?}", stack); // Peek at top without removing if let Some(&top) = stack.last() { println!("Top: {}", top); } }
Stack complexity analysis
Using Vec<T> as a stack:
| Operation | Time Complexity | Why |
|---|---|---|
push(x) | O(1)* | Add to end (*amortized) |
pop() | O(1) | Remove from end |
last() (peek) | O(1) | Just read last element |
is_empty() | O(1) | Check if len == 0 |
Space: O(n) where n = number of elements
Perfect for stack! All operations are constant time.
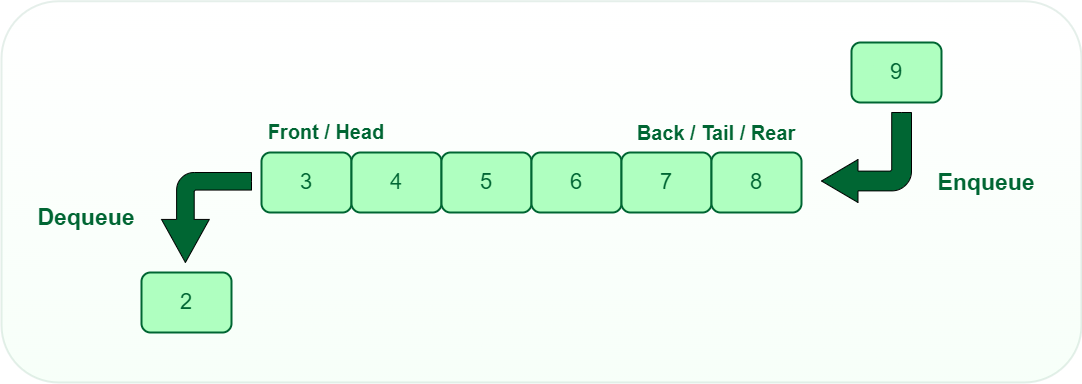
Our next data structure: What is a queue?
Think of: Line at a store, print queue, airport security
Operations:
- Enqueue: Add item to the back
- Dequeue: Remove item from the front
- Front/Peek: Look at front item
Key property: FIFO - First thing in is the first thing out
Real-world queue applications
Simulations:
- Customers arriving at a bank
- Cars at a traffic light
- Hospital emergency room triage
Task scheduling:
- Operating system process scheduling
- Printer job queues
Buffering:
- Keyboard input buffer
- Video/audio streaming
Breadth-First Search (BFS) (coming in Lecture 36!)
- Explore graph level by level
- Use queue to track which nodes to visit next
Problem: Using Vec as a queue is slow!
Naive approach:
#![allow(unused)] fn main() { let mut queue = Vec::new(); queue.push(1); // Add to back - O(1) queue.push(2); queue.push(3); let first = queue.remove(0); // Remove from front - O(n) }
Question: Why is removing the first value O(n)?
We need a better structure!
Enter VecDeque: Double-ended queue
VecDeque = "Vec Deque" = Double-ended queue (pronounced "vec-deck")
Key idea: Circular buffer - can efficiently add/remove from BOTH ends!
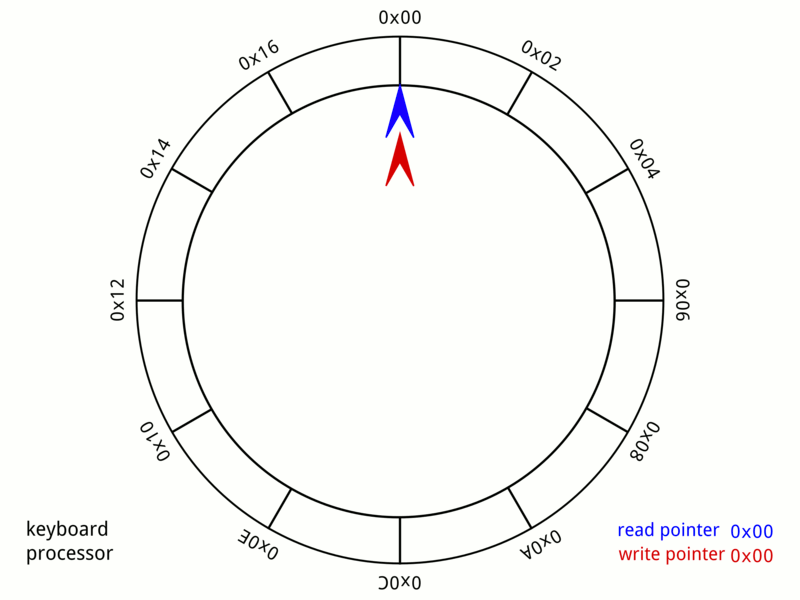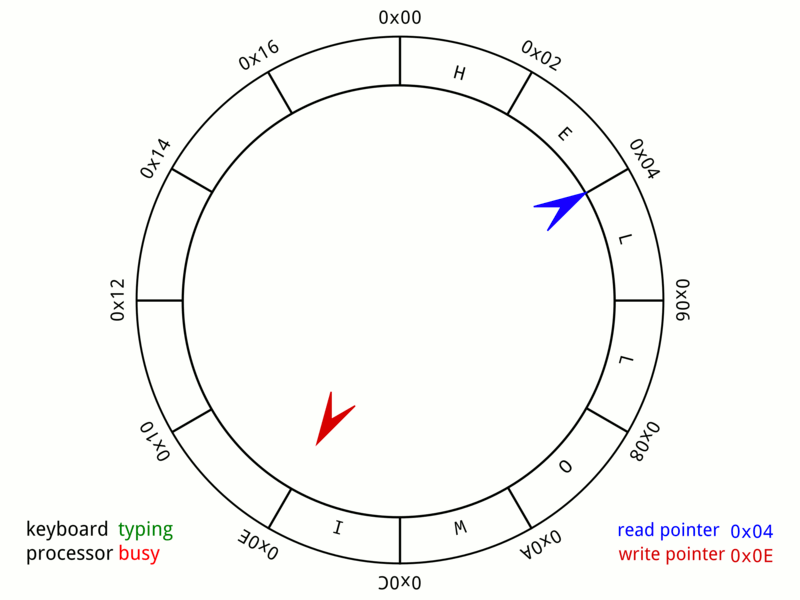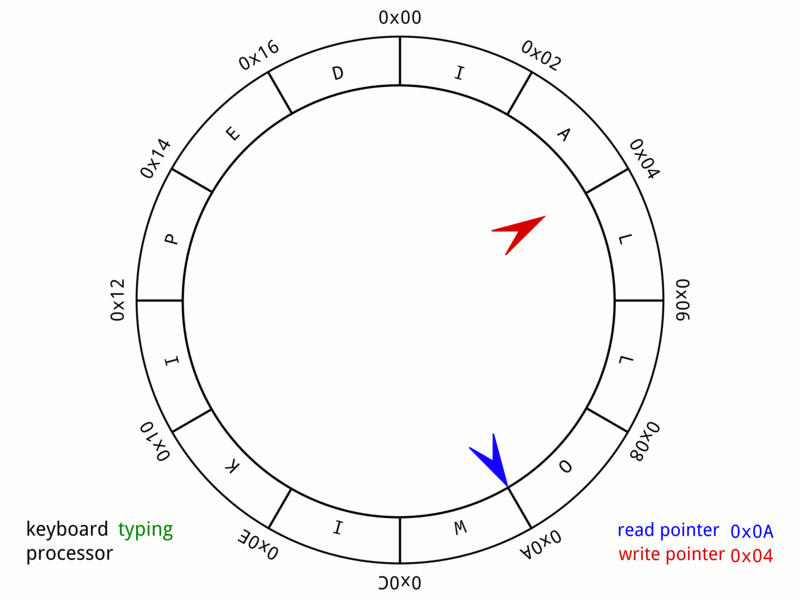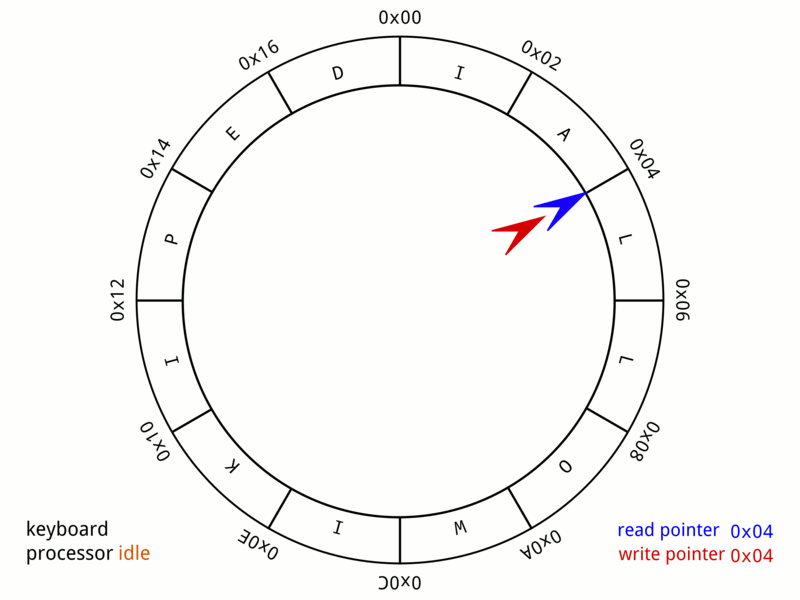
use std::collections::VecDeque; fn main() { let mut queue: VecDeque<i32> = VecDeque::new(); // Enqueue (add to back) queue.push_back(1); queue.push_back(2); queue.push_back(3); println!("Queue: {:?}", queue); // [1, 2, 3] // Dequeue (remove from front) if let Some(front) = queue.pop_front() { println!("Dequeued: {}", front); // 1 } println!("Queue: {:?}", queue); // [2, 3] }
How VecDeque works: Circular buffer / "growable ring buffer"
Conceptual model: Array with front and back pointers that wrap around
Capacity 8 buffer:
[_, _, 1, 2, 3, _, _, _]
^ ^
front back
After push_back(4):
[_, _, 1, 2, 3, 4, _, _]
^ ^
front back
After pop_front():
[_, _, _, 2, 3, 4, _, _]
^ ^
front back
After push_back(5), push_back(6):
[_, _, _, 2, 3, 4, 5, 6]
^ ^
back front
After push_back(7) - wraps around!
[7, _, _, 2, 3, 4, 5, 6]
^ ^
back front
After push_back(8):
[7, 8, _, 2, 3, 4, 5, 6]
^ ^
back front
Clever! Both ends can grow/shrink in O(1) time without shifting elements.
VecDeque complexity analysis
| Operation | Time Complexity | Why |
|---|---|---|
push_back(x) | O(1)* | Add to back |
push_front(x) | O(1)* | Add to front |
pop_back() | O(1) | Remove from back |
pop_front() | O(1) | Remove from front |
get(i) | O(1) | Random access (translated index) |
*Amortized - occasionally needs to resize
Perfect for queues! Efficient operations on both ends.
Think about: Vec vs VecDeque
When to use Vec:
- Only adding/removing from end (stack)
- Slightly faster access
When to use VecDeque:
- Adding/removing from front (queue)
- Adding/removing from both ends (deque)
- Don't mind slightly more complex memory layout
What is a deque?
Deque = Double-Ended Queue (pronounced "deck")
Operations: Can add/remove from BOTH front and back
push_front(x),push_back(x)pop_front(),pop_back()front(),back()to view
More general than stack or queue
- Use as stack: only use back operations
- Use as queue: push_back, pop_front
- Use as deque: use any combination
Rust doesn't have a separate queue type you just use VecDeques for both queues and deques
Deque applications
1. Undo/Redo with limits:
- Can remove oldest undo if stack gets too large
2. Palindrome checking:
- Compare elements from both ends moving inward
- Efficient with deque: pop_front and pop_back
3. Sliding window algorithms:
- Maintain elements in a window that slides across data
- Add to back, remove from front (queue)
- Sometimes remove from back too (deque)
Think-pair-share: Matching problems to structures
Which data structure would you use?
- Browser history (forward/back button)
- Drownloading a bunch of dropbox files
- Undo/redo keyboard shortcuts
- Recent files list
Another linear structure: Linked lists
So far we've seen:
Vec<T>- contiguous array, great for stack operationsVecDeque<T>- circular buffer, great for queue/deque operations
Another option: Linked lists
What is a linked list?
- Each element (node) contains data + pointer to next element
- Elements can be anywhere in memory (not contiguous)
- Singly linked: pointer to next only
- Doubly linked: pointers to both next and previous
Singly linked list:
[data|next] → [data|next] → [data|next] → None
Doubly linked list:
None ← [prev|data|next] ↔ [prev|data|next] ↔ [prev|data|next] → None
When to use:
- O(1) insertion/deletion in middle (if you have a pointer there)
- Don't need random access by index
- Memory fragmentation is okay
In Rust:
- Rust has
std::collections::LinkedList(doubly-linked) - Rarely used in practice! Why?
- Ownership makes linked lists complex to implement
- Losing get-by-index is a high price to pay
Bottom line: Know linked lists exist, but prefer Vec or VecDeque in Rust (and most other modern languages)!
Summary: Stacks vs queues vs deques
| Structure | Access Pattern | Rust Type | Use When |
|---|---|---|---|
| Stack | LIFO (Last In, First Out) | Vec<T> | Undo, function calls, DFS, parsing |
| Queue | FIFO (First In, First Out) | VecDeque<T> | Task scheduling, BFS, buffering |
| Deque | Both ends | VecDeque<T> | Sliding window, flexible use |
| Operation | Vec | VecDeque | LinkedList |
|---|---|---|---|
| Push back | O(1)* | O(1)* | O(1) |
| Pop back | O(1) | O(1) | O(1) |
| Push front | O(n) | O(1) | O(1) |
| Pop front | O(n) | O(1) | O(1) |
| Insert middle | O(n) | O(n) | O(1)** |
| Random access | O(1) | O(1) | O(n) |
*Amortized
**Given a pointer
Rule: If you need front operations, use VecDeque. Otherwise, Vec is simpler.
Comparison: Sequential vs Hash-based Collections
Sequential (Vec/VecDeque):
- Elements stored in order
- Access by position/index
Hash-based (HashMap/HashSet):
- Elements stored by hash value
- Access by key/value equality
Sequential vs Hash: Operation comparison
| Operation | Vec/VecDeque | HashMap/HashSet |
|---|---|---|
| Check contains | O(n) - must search | O(1)* - hash lookup |
| Remove/Insert element | O(n) - must shift | O(1)* |
| Access by index | O(1) - vec[i] | N/A |
| Iterate in consistent order | Yes | No (and slower) |
| Can Sort | Yes | No |
| Can Have Duplicates | Yes | No |
| Storage Complexity | 1x | ~1.5-2x |
| Type compatibility | All | Hashable (no floats) |
*Amortized, assuming good hash function
Activity time
See gradescope / our website / Rust Playground