Lecture 37 - Topological sort & minimum spanning trees
Logistics
- HW7 due tonight
- HW6 graded - corrections due in a week
- Monday is the last class with new material (shortest path algorithms)
- Tuesday discussion and Wednesday lecture will be review
- Final exam is 12pm-2 on Wed, 12/17
Learning objectives
We're covering two problems and three algorithms today -
Problems:
- Topological sorting
- Minimum spanning trees
Algorithms:
- Topological sorting using DFS
- Kruskal's for MST
- Prim's for MST
You'll learn:
- The motivations for each problem
- The high-level algorithm for each problem
- The time complexity of these algorithms
First, a formal definition of DAG
DAG = Directed Acyclic Graph
Directed: Edges have direction (one-way) Acyclic: No cycles (can't loop back to yourself)
Example DAG:
A → B → D
↓ ↓
C → E
Not a DAG (has cycle):
A → B → D
↑ ↓
C ← E
Why DAGs matter
DAGs model dependencies!
Real-world examples:
-
Course prerequisites
- DS110 must come before DS210
- Can't have circular prerequisites
-
Build systems
- File A depends on B and C
- Compile in correct order
-
Project scheduling
- Task B can't start until Task A finishes
-
Spreadsheet calculations
- Cell D1 = A1 + B1
- Calculate in dependency order
Topological sorting
Problem: Given a DAG, find an ordering of vertices such that for every edge u → v, u comes before v in the ordering.
Example: Course prerequisites
CS101 → CS201 → CS301
↓ ↓
CS102 → CS202
Valid topological orderings:
- CS101, CS102, CS201, CS202, CS301
- CS101, CS201, CS102, CS202, CS301
- CS101, CS102, CS202, CS201, CS301
This is only possible for DAGs!
- If there's a cycle, no valid ordering exists
Intuition: "What order should I do tasks that have dependencies?"
Topological sort examples
Graph (build dependencies):
libA → app
↓ ↑
libB
Meaning:
- app depends on libA and libB
- libB depends on libA
Topological order: libA, libB, app
- Build libA first (no dependencies)
- Then libB (depends on libA)
- Then app (depends on both)
Topological sort examples
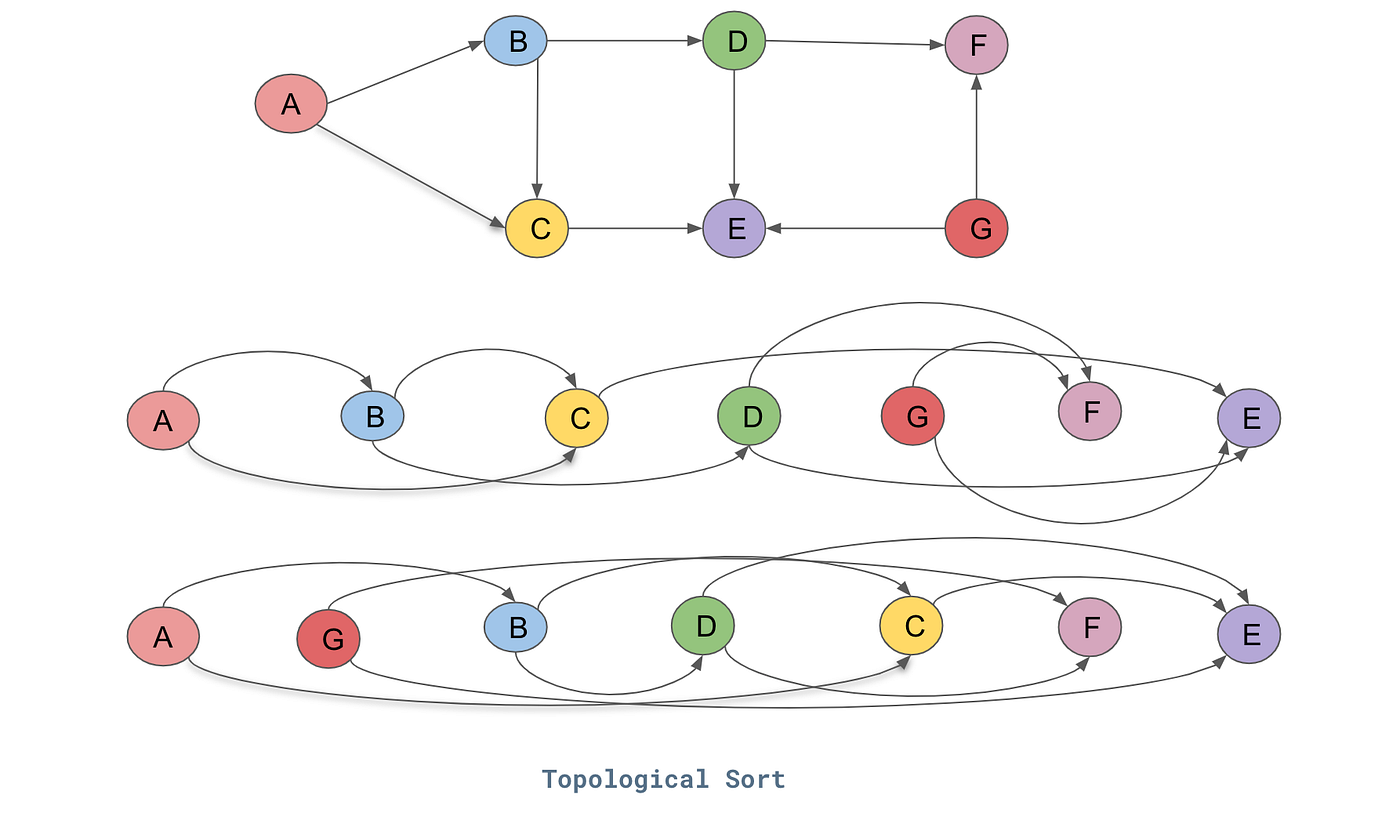
Algorithm: DFS-based topological sort
Main idea: Use DFS, add vertex to result AFTER exploring all descendants
Algorithm:
- Run DFS from each unvisited vertex
- When finishing a vertex (after visiting all descendants), add to result
- Reverse the result
Why reverse? We add vertices as we finish them (deepest first), but want dependencies first
Topological sort example trace
Graph:
A → B → D
↓ ↓
C → E
DFS from A:
Visit A:
Visit B:
Visit D:
D has no neighbors, finish D → add D to list [D]
Visit E:
E has no neighbors, finish E → add E to list [D, E]
Finish B → add B to list [D, E, B]
Visit C:
E already visited
Finish C → add C to list [D, E, B, C]
Finish A → add A to list [D, E, B, C, A]
Reverse: [A, C, B, E, D]
Check:
A → B: A comes before B
A → C: A comes before C
B → D: B comes before D
B → E: B comes before E
C → E: C comes before E
Implementation in Rust
use std::collections::HashSet; fn dfs_topo( graph: &Vec<Vec<usize>>, vertex: usize, visited: &mut HashSet<usize>, result: &mut Vec<usize> ) { visited.insert(vertex); for &neighbor in &graph[vertex] { if !visited.contains(&neighbor) { dfs_topo(graph, neighbor, visited, result); } } // Add to result AFTER visiting all descendants result.push(vertex); } fn topological_sort(graph: &Vec<Vec<usize>>) -> Vec<usize> { let mut visited = HashSet::new(); let mut result = Vec::new(); // Try starting from each unvisited vertex for vertex in 0..graph.len() { if !visited.contains(&vertex) { dfs_topo(graph, vertex, &mut visited, &mut result); } } // Reverse because we added in finish order result.reverse(); result } fn main() { // Graph: 0 → 1 → 3 // ↓ ↓ // 2 → 4 let graph = vec![ vec![1, 2], // 0 → 1, 2 vec![3, 4], // 1 → 3, 4 vec![4], // 2 → 4 vec![], // 3 → nothing vec![], // 4 → nothing ]; let order = topological_sort(&graph); println!("Topological order: {:?}", order); // Possible output: [0, 2, 1, 4, 3] or [0, 1, 2, 3, 4], etc. }
Detecting cycles with topological sort
What if graph has a cycle?
Modified algorithm: Track vertices in current DFS path
- If we visit a vertex already in current path, there's a cycle!
#![allow(unused)] fn main() { fn has_cycle_dfs( graph: &Vec<Vec<usize>>, vertex: usize, visited: &mut HashSet<usize>, in_path: &mut HashSet<usize> ) -> bool { visited.insert(vertex); in_path.insert(vertex); for &neighbor in &graph[vertex] { if in_path.contains(&neighbor) { return true; // Cycle detected! } if !visited.contains(&neighbor) { if has_cycle_dfs(graph, neighbor, visited, in_path) { return true; } } } in_path.remove(&vertex); // Done with this path false } }
Topological sort complexity
Time complexity:
- DFS visits each vertex once: O(V)
- DFS explores each edge once: O(E)
- Reversing result: O(V)
- Total: O(V + E)
Space complexity:
- Visited set: O(V)
- Result list: O(V)
- Recursion stack: O(V)
- Total: O(V)
Efficient! Same as regular DFS
Applications of topological sort
1. Task scheduling
- Schedule tasks respecting dependencies
- Critical path analysis
2. Build systems
- Compile files in correct order (Make, Cargo)
3. Package dependency resolution
- Install packages in order (npm, pip, cargo)
4. Spreadsheet evaluation
- Calculate cells in dependency order
Think-pair-share: Review quiz 1
Question 1: What is the time complexity of searching for a specific value in a balanced BST with n nodes?
- A) O(1)
- B) O(log n)
- C) O(n)
- D) O(n log n)
Question 2: Which data structure would be most efficient for implementing a priority queue?
- A) Vec
- B) VecDeque
- C) BinaryHeap
- D) HashMap
Question 3: In a max-heap, what is the relationship between a parent and its children?
- A) Parent < both children
- B) Parent > both children
- C) Parent = both children
- D) Parent < one child and > the other child
Minimum spanning trees: Connecting everything cheaply
Problem: Given a weighted, undirected graph, find a subset of edges that:
- Connects all vertices (spanning)
- Forms a tree (no cycles)
- Has minimum total weight
Example: Build road network connecting cities with minimum total cost
Spanning trees
A Spanning Tree is a subgraph that:
- Includes all vertices
- Is connected (can reach any vertex from any other)
- Has no cycles (is a tree)
- Has exactly V-1 edges (property of trees)
Example graph with 4 vertices:
Original graph (weights):
A --2-- B
| \ |
5 3 4
| \ |
C --1-- D
Possible spanning trees:
Tree 1: Tree 2: Tree 3:
A--2--B A--2--B A B
| | | | 3/ |
5 4 5 5 \ 4
| | | | |
C--1--D C--1--D C--1--D
Weight: 12 Weight: 8 Weight: 13
↑ MST!
Minimum spanning tree (MST)
MST: The spanning tree with minimum total edge weight
Properties:
- Not unique (multiple MSTs can exist with same weight)
- Always has V-1 edges
- Connects all vertices
- Total weight is minimized
Applications:
- Network design (minimize cable length)
- Approximation algorithms (TSP)
- Clustering (cut MST edges to create clusters)
Think about: How to find MST?
Greedy approaches:
- Start with cheapest edge, keep adding cheapest edge that doesn't create cycle?
- Start from a vertex, keep adding cheapest edge to new vertex?
Both work! These are Kruskal's and Prim's algorithms.
Kruskal's algorithm idea
Strategy: Add edges in order of increasing weight, skip edges that create cycles
High-level:
- Sort all edges by weight
- Start with empty graph (just vertices)
- For each edge (in order):
- If adding it doesn't create a cycle, add it
- Otherwise, skip it
- Stop when we have V-1 edges
Graph:
A --2-- B
| \ |
5 3 4
| \ |
C --1-- D
Edges sorted by weight: (C-D, 1), (A-B, 2), (A-D, 3), (B-D, 4), (A-C, 5)
Steps:
Step 1: Add (C-D, 1) - no cycle
C--1--D
Step 2: Add (A-B, 2) - no cycle
A--2--B
C--1--D
Step 3: Add (A-D, 3) - no cycle
A--2--B
|
3
|
C--1--D
Step 4: Skip (B-D, 4) - would create cycle A-B-D-A
Step 5: Skip (A-C, 5) - would create cycle A-D-C-A
Done! MST weight = 1 + 2 + 3 = 6
How to detect cycles efficiently?
Challenge: Need to quickly check if adding an edge creates a cycle
Solution: Union-Find (Disjoint Set Union)
Idea: Track which vertices are in the same connected component
- Find(v): Which component is v in?
- Union(u, v): Merge components containing u and v
- Cycle check: If u and v in same component, edge creates cycle!
Complexity: Near constant time
Kruskal's implementation (conceptual)
#![allow(unused)] fn main() { // Pseudocode - Union-Find implementation omitted for clarity fn kruskal(vertices: usize, edges: Vec<(usize, usize, i32)>) -> Vec<(usize, usize, i32)> { let mut mst = Vec::new(); let mut uf = UnionFind::new(vertices); // Sort edges by weight let mut edges = edges; edges.sort_by_key(|&(_, _, weight)| weight); for (u, v, weight) in edges { // If u and v not in same component, add edge if uf.find(u) != uf.find(v) { mst.push((u, v, weight)); uf.union(u, v); if mst.len() == vertices - 1 { break; // Have V-1 edges, done! } } } mst } }
Kruskal's complexity
Time complexity:
- Sort edges: O(E log E)
- Union-Find operations: O(E × a(V)) ≈ O(E) where a is inverse Ackermann (nearly constant)
- Total: O(E log E)
Space complexity:
- Union-Find structure: O(V)
- Edge list: O(E)
- Total: O(V + E)
Note: O(E log E) = O(E log V) since E ≤ V^2 → log E ≤ 2 log V
Prim's algorithm idea
Strategy: Grow MST from a starting vertex, always adding the cheapest edge to a new vertex
High-level:
- Start with arbitrary vertex in MST
- Repeat:
- Find the cheapest edge connecting MST to a non-MST vertex
- Add that edge and vertex to MST
- Stop when all vertices in MST
Greedy! Always expand MST with cheapest available edge.
Prim's example
Graph:
A --2-- B
| \ |
5 3 4
| \ |
C --1-- D
Start at A:
Step 1: MST = {A}
Edges from MST: (A-B, 2), (A-D, 3), (A-C, 5)
Add cheapest: (A-B, 2)
MST = {A, B}
Step 2: MST = {A, B}
Edges from MST: (A-D, 3), (B-D, 4), (A-C, 5)
Add cheapest: (A-D, 3)
MST = {A, B, D}
Step 3: MST = {A, B, D}
Edges from MST: (D-C, 1), (B-D, skip - both in MST), (A-C, 5)
Add cheapest: (D-C, 1)
MST = {A, B, D, C}
Done! All vertices in MST.
Total weight = 2 + 3 + 1 = 6
Prim's implementation strategy
Use a priority queue (min-heap)!
Algorithm:
- Start with arbitrary vertex, add its edges to priority queue
- While priority queue not empty:
- Extract minimum edge
- If it connects to new vertex:
- Add vertex to MST
- Add its edges to priority queue
- Continue until all vertices in MST
Similar to Dijkstra's (next lecture!), but choosing edges instead of paths
Prim's complexity
Time complexity:
- Each vertex added to MST once: O(V)
- Each edge considered once: O(E)
- Each edge added/removed from heap: O(log E) = O(log V)
- Total: O(E log V) with binary heap
Space complexity:
- Priority queue: O(E)
- MST tracking: O(V)
- Total: O(E)
Note: Can be improved to O(E + V log V) with Fibonacci heap (advanced!)
Think-pair-share: Review quiz 2
Question 4: Which data structure should you use if you need to frequently add/remove elements from both ends?
- A) Vec
- B) VecDeque
- C) LinkedList
- D) HashMap
Question 5: What is the difference between BFS and DFS traversal of a graph?
- A) BFS uses a queue, DFS uses a stack
- B) BFS uses a stack, DFS uses a queue
- C) BFS is always faster than DFS
- D) DFS always finds the shortest path
Question 6: In an adjacency list representation of a graph with V vertices and E edges, what is the space complexity?
- A) O(V)
- B) O(E)
- C) O(V + E)
- D) O(V²)
Kruskal vs Prim
| Property | Kruskal | Prim |
|---|---|---|
| Strategy | Add cheapest edge globally | Grow from starting vertex |
| Data structure | Union-Find | Priority Queue |
| Time | O(E log E) | O(E log V) |
| Works on | Disconnected graphs too | Connected graphs |
| Good for | Sparse graphs | Dense graphs |
Both produce correct MST! Choice is mostly implementation preference.
MST applications
1. Network design
- Minimize cable length connecting buildings
- Design low-cost communication networks
2. Approximation algorithms
- 2-approximation for TSP (traveling salesman)
3. Clustering
- Remove longest edges from MST to create clusters
4. Image segmentation
- Pixels as vertices, similarity as weights