Complexity Analysis: Understanding Algorithm Performance

About This Module

This module covers algorithmic complexity analysis with a focus on how memory is managed in Rust vectors. You'll learn to analyze time and space complexity of operations and understand the performance characteristics of different data structures and algorithms.

Prework

Prework Reading

Please read the following:

• (review) Chapter 8.1: Storing Lists of Values with Vectors
• (optional) Additional reading: Wikipedia: Analysis of Algorithms

Pre-lecture Reflections

1. What is the difference between time complexity and space complexity?
2. Why is amortized analysis important for dynamic data structures?
3. How does Rust's memory management affect algorithm complexity?

Learning Objectives

By the end of this module, you will be able to:

• Analyze time and space complexity using Big O notation
• Understand amortized analysis for vector operations
• Compare complexity of some algorithms and data structures

Complexity Analysis (e.g. memory management in vectors)

Let's dive deeper into algorithmic complexity analysis by considering how memory is manged in Rust Vecs.

Previously: vectors Vec<T>

• Dynamic-length array/list
• Allowed operations:
  • access item at specific location
  • push: add something to the end
  • pop: remove an element from the end

Other languages:

• Python: list
• C++: vector<T>
• Java: ArrayList<T> / Vector<T>

Implementation details

Challenges

• Size changes: allocate on the heap?
• What to do if a new element added?
  • Allocate a larger array and copy everything?
  • Linked list?

Solution

• Allocate more space than needed!
• When out of space:
  • Increase storage size by, say, 100%
  • Copy everything

Under the hood

Variable of type Vec<T> contains:

• pointer to allocated memory
• size: the current number of items
• capacity: how many items could currently fit

Important: size $\le$ capacity

Example (adding elements to a vector)

Method capacity() reports the current storage size

#![allow(unused)]
fn main() {
// print out the current size and capacity

// define a generic function `info` that takes one argument, `vector`,
// of generic `Vec` type and prints it's length and capacity
fn info<T>(vector:&Vec<T>) {  
    println!("length = {}, capacity = {}",vector.len(),vector.capacity());
}

// Let's keep adding elements to Vec and see what happens to capacity

let mut v = Vec::with_capacity(7); // instantiate empty Vec with capacity 7
let mut capacity = v.capacity();
info(&v);

for i in 1..=1000 {
    v.push(i);  // push the index onto the Vec

    // if capacity changed, print the length and new capacity
    if v.capacity() != capacity {
        capacity = v.capacity();
        info(&v);
    }
};
info(&v);
}

Example (decreasing the size of a vector)

#![allow(unused)]
fn main() {
fn info<T>(vector:&Vec<T>) {  
    println!("length = {}, capacity = {}",vector.len(),vector.capacity());
}
// what happens when we decrease the Vec by popping off values?

let mut v = vec![10; 1000];

info(&v);

// `while let` is a control flow construct that will continue
// as long as pattern `Some(_) = v.pop()` matches.
// If there is a value to pop, v.pop() returns Option enum, which
//    is either Some(Vec<T>)
//    otherwise it will return None and the loop will end.
while let Some(_) = v.pop() {}

info(&v);
}

Questions

• What is happening as we push elements?
• When does it happen?
• How much is it changing by?
• What happens when we pop? Is capacity changing?

Example -- Shrink to Fit

• We can shrink the size of a vector manually

#![allow(unused)]
fn main() {
fn info<T>(vector:&Vec<T>) {  
    println!("length = {}, capacity = {}",vector.len(),vector.capacity());
}

let mut v = vec![10; 1000];
while let Some(_) = v.pop() {}

info(&v);

for i in 1..=13 {
    v.push(i);
}

info(&v);

// shrink the size manually
v.shrink_to_fit();

info(&v);
}

Note: size and capacity not guaranteed to be the same

Example -- Creating a vector with specific capacity

Avoid reallocation if you know how many items to expect.

#![allow(unused)]
fn main() {
fn info<T>(vector:&Vec<T>) {  
    println!("length = {}, capacity = {}",vector.len(),vector.capacity());
}

// creating vector with specific capacity
let mut v2 : Vec<i32> = Vec::with_capacity(1234);
info(&v2);
}

.get() versus .pop()

• .get() does not remove from the vector, but you must specify the index
• .pop() removes the last element from the vector
• both return an Option<T>
  • .get() returns Some(T) if the index is valid, None otherwise
  • .pop() returns Some(T) if the vector is not empty, None otherwise

#![allow(unused)]
fn main() {
let mut v = Vec::new();
for i in 1..=13 {
    v.push(i);
}
println!("{:?}", v);

// Does not remove from the vector, but you must specify the index
println!("{:?} {:?}", v.get(v.len()-1), v);

// But this one does, and removes the last element
println!("{:?} {:?}", v.pop(), v);
}

Other useful functions

• append Add vector at the end of another vec.append(&mut vec2)
• clear Remove all elements from the vector vec.clear()
• dedup Remove consecutive identical elements vec.dedup(), most useful when combined with sort
• drain Remove a slice from the vector vec.drain(2..4) -- removes and shifts -- expensive
• remove Remove an element from the vector vec.remove(2) -- removes and shifts -- expensive
• sort Sort the elements of a mutable vector vec.sort()
• Complete list at https://doc.rust-lang.org/std/vec/struct.Vec.html

Sketch of analysis: Amortization

• Inserting an element not constant time (i.e. $O(1)$) under all conditions

However

• Assumption: allocating memory size $n$ takes either $O(n)$ or $O(1)$ time

• Slow operations: $O($ current_size $)$ time

• Fast operations: $O(1)$ time

What is the average time?

• Consider an initial 100-capacity Vec.
• Continually add element
• First 100 added elements: $O(1)$
• For 101st element: $O(n)$

So on average for the first 101 elements: $(100\cdot 1+1\cdot 100)/101\approx 2$

• On average: $O(1)$ amortized time
• Fast operations pay for slow operations

Dominant terms and constants in $O()$ notation

We ignore constants and all but dominant terms as $n\to \infty$ :

$$O(n/2)\to O(n)$$

$$O(n^2+100n+50)\to O(n^2)$$

$$O(2^n+n^{10})\to \text{?}$$

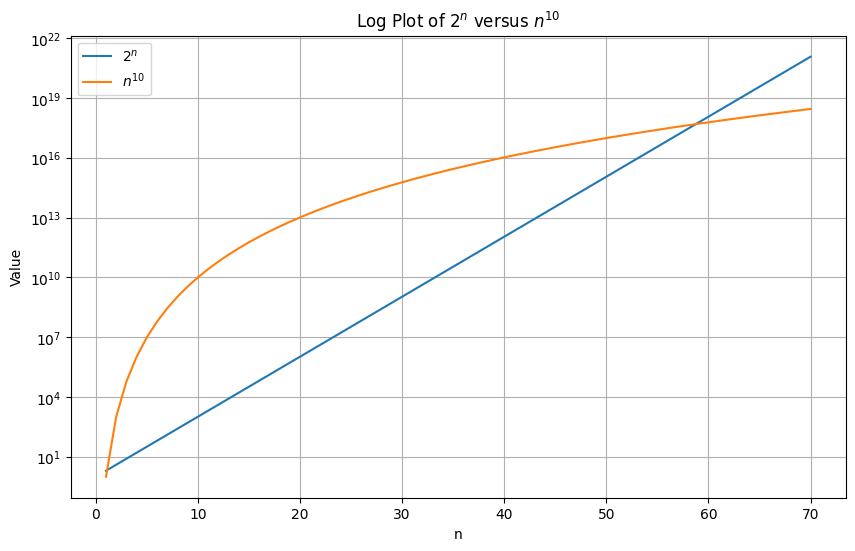
Which is worse? $2^n$ or $n^{10}$?

Shrinking?

• Can be implemented this way too
• Example: shrink by 50% if less than 25% used
• Most implementations don't shrink automatically

Notations

$O(n)$ -> Algorithm takes no more than n time (worst case scenario)

$\Omega (n)$ -> Algorithm takes at least n time (best case scenario)

$\Theta (n)$ -> Average/Typical running time for the algorithm (average case scenario)

Digression (Sorting Vectors in Rust)

Sorting on on integer vectors works fine.

#![allow(unused)]
fn main() {
// This works great
let mut a = vec![1, 4, 3, 6, 8, 12, 5];
a.sort();
println!("{:?}", a);
}

But sorting on floating point vectors does not work directly.

#![allow(unused)]
fn main() {
// But the compiler does not like this one, since sort depends on total order
let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0];

a.sort();
println!("{:?}", a);
}

Why?

Because floats in Rust support special values like NaN and inf which don't obey normal sorting rules.

More technically, floats in Rust don't implement the Ord trait, only the PartialOrd trait.

The Ord trait is a total order, which means that for any two numbers $x$ and $y$, either $x<y$, $x>y$, or $x==y$.

The PartialOrd trait is a partial order, which means that for any two numbers $x$ and $y$, either $x<y$, $x>y$, $x==y$, or the comparison is not well defined.

Example -- inf

#![allow(unused)]
fn main() {
let mut x: f64 = 6.8;
println!("{}", x/0.0);
}

We can push inf onto a Vec.

#![allow(unused)]
fn main() {
let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0];
let mut x: f64 = 6.8;
a.push(x/0.0);
a.push(std::f64::INFINITY);
println!("{:?}", a);
}

Example -- NaN

#![allow(unused)]
fn main() {
let mut x: f64 = -1.0;
println!("{}", x.sqrt());
}

Similarly, we can push NaN onto a Vec.

#![allow(unused)]
fn main() {
let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0];
let mut x: f64 = -1.0;
a.push(x.sqrt());
a.push(std::f64::NAN);
println!("{:?}", a);
}

Example -- Sorting with sort_by()

We can work around this by:

• not relying on the Rust implementation of sort(), but rather
• defining our own comparison function using partial_cmp, which is a required method for the PartialOrd trait, and
• using the .sort_by() function.

#![allow(unused)]
fn main() {
// This is ok since we don't use sort, sort_by depends on the function you pass in to compute order
let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0];
// a.sort();
a.sort_by(|x, y| x.partial_cmp(y).unwrap());
println!("{:?}", a);
}

where partial_cmp is a method that returns for types that implement the PartialOrd trait:

• Some(std::cmp::Ordering::Equal) when $x==y$,
• Some(std::cmp::Ordering::Less) when $x<y$
• Some(std::cmp::Ordering::Greater) when $x>y$
• None when the comparison is not well defined, e.g x ? NaN

Example -- Can even handle inf

#![allow(unused)]
fn main() {
let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, std::f32::INFINITY, 6.0, 8.0, 12.0, 5.0];

println!("{:?}", a);

a.sort_by(|x, y| x.partial_cmp(y).unwrap());
println!("{:?}", a);
}

#![allow(unused)]
fn main() {
let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, std::f32::INFINITY, 6.0, std::f32::NEG_INFINITY, 8.0, 12.0, 5.0];

println!("{:?}", a);

a.sort_by(|x, y| x.partial_cmp(y).unwrap());
println!("{:?}", a);
}

#![allow(unused)]
fn main() {
let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, std::f32::INFINITY, 6.0, 8.0, std::f32::INFINITY, 12.0, 5.0];

println!("{:?}", a);

a.sort_by(|x, y| x.partial_cmp(y).unwrap());
println!("{:?}", a);
}

Infinity goes to the end:

Infinity has a well-defined ordering in IEEE 754 floating-point arithmetic:

• Positive infinity is explicitly defined as greater than all finite numbers
• inf.partial_cmp(finite_number) returns Some(Ordering::Greater)
• This is a valid comparison, so the unwrap_or fallback is never used
• Result: infinity naturally sorts to the end

Just be careful!

It will panic if you try to unwrap a special value like NaN.

#![allow(unused)]
fn main() {
// When partial order is not well defined in the inputs you get a panic
let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0];

let mut x: f32 = -1.0;
x = x.sqrt();
a.push(x);

println!("{:?}", a);
a.sort_by(|x, y| x.partial_cmp(y).unwrap());
println!("{:?}", a);
}

Workaround

Return a default value when the comparison is not well defined.

#![allow(unused)]
fn main() {
// When partial order is not well defined in the inputs you get a panic
let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0];

// push a NaN (sqrt(-1.0))
let mut x: f32 = -1.0;
x = x.sqrt();
a.push(x);

// push an inf (10.0/0.0)
a.push(10.0/0.0);

println!("{:?}", a);

a.sort_by(|x, y| x.partial_cmp(y).unwrap_or(std::cmp::Ordering::Less));
println!("{:?}", a);
}

NaN goes to the beginning:

The .unwrap_or(std::cmp::Ordering::Less) says: "if the comparison is undefined (returns None), pretend that x is less than y".

So when NaN is compared with any other value:

• NaN.partial_cmp(other) → None
• Falls back to Ordering::Less
• This means NaN is always treated as "smaller than" everything else
• Result: NaN gets sorted to the beginning

In-Class Piazza Poll

Select all that are true:

1. The push() operation on a Rust Vec<T> always has O(1) time complexity in the worst case.
2. When a Vec<T> runs out of capacity and needs to grow, it typically doubles its capacity, resulting in O(n) time for that specific push operation where n is the current size.
3. The pop() operation on a Rust Vec<T> has O(1) time complexity and automatically shrinks the vector's capacity when the size drops below 25% of capacity.
4. The amortized time complexity of push() operations on a Vec<T> is O(1), meaning that averaged over many operations, each push takes constant time.
5. In Big O notation, O(n² + 100n + 50) simplifies to O(n²) because we ignore constants and non-dominant terms as n approaches infinity.