Greedy algorithms

About This Module

Prework

Prework Reading

Pre-lecture Reflections

Lecture

Learning Objectives

Greedy algorithms

• Make locally best (or any) decision towards solving a problem

Warm Up: Coin Change Problem

You are a cashier and you need to give US $0.43 back to your customer.

Problem: We want to find the smallest number of coins that sum up to a given value.

Assumption: We're not limited by number of coins in any denomination.

Input: Set of coin denominations, Target value

Output: Minimal set of coins adding up to value

What would a greedy approach look like here?

Idea: Pick the largest denomination for the remaining value and repeat until done.


Let's try it out.

fn coin_change(denominations: &[usize], value: usize) {
    // Arguments:
    // denominations: list of coin denominations sorted in decreasing value
    // value: target value we are trying to match

    // count notes using Greedy approach
    let mut coin_counter = vec![0; denominations.len()];
    
    let mut remainder = value;
    for i in 0..denominations.len() {
        // will at least one of the current denomination work?
        if remainder >= denominations[i] {
            // check how many of denomination i we can use.
            coin_counter[i] = remainder / denominations[i];
            remainder = remainder % denominations[i];
        }
    }
     
    // Print notes
    println!("Currency Count ->");
    for i in 0..denominations.len() {
        if coin_counter[i] != 0 {
            println!("{} : {}", denominations[i], coin_counter[i]);
        }
    }
}

let denoms = [25,10,5,1];  // US coin denominations in decreasing order
let val = 41;
coin_change(&denoms, val);

Currency Count ->
25 : 1
10 : 1
5 : 1
1 : 1

// lets try a different set of denominations
let denoms = [25,15,1];
let val = 30;
coin_change(&denoms, val);

Currency Count ->
25 : 1
1 : 5

Warning: The greedy approach is only optimal for certain sets of denominations! These are known as canonical coin systems.

Canonical Coin System:

For the greedy algorithm to work correctly and always give the minimum number of coins, the coin denominations must have the following property:

• The denominations must be in a "canonical" system, meaning that each coin value is at least twice the value of the next smaller denomination.

This fails because 25 is not at least twice the value of 15.

When this property doesn't hold (like in our example with [25, 15, 1]), we need to use a more sophisticated algorithm like dynamic programming to find the optimal solution.

Is there a country with an non-canonical coin system?

// United Kingdom before decimalization in 1971
let denoms = [30,24,12,6,3,1];
let val = 48;
coin_change(&denoms, val);

Currency Count ->
30 : 1
12 : 1
6 : 1

We could have done better with 2x 24p.

Data science connection in a future lecture

• Heuristics for creating decision trees
  • select "best" single split and recurse

Example we have seen

• Shortest paths (Dijkstra's algorithm)
  • select the vertex known to be closest
  • try routing paths through it
  • Gives globally optimal solution!!!

Another Example: Minimum spanning tree

Find cheapest overall subset of edges so that the graph is connected

• Kruskal's algorithm: keep adding the cheapest edge that connects disconnected groups vertices

• Complexity $O(E\ast log(E))$

Why is MST useful?

• Connecting N locations with fiber using the least amount of fiber

• Traveling salesman approximate solution

Algorithm Outline

Start with a graph with weighted edges.

Disconnect all edges...

1. Find the cheapest edge remaining
2. Look at the 2 nodes it connects and find the root of the tree they belong to
3. If they belong to the same tree go back to step 1
4. Else join the two trees into a single tree

Define Graph Structure

We'll define a modified graph structure that simultaneously represents a weighted undirected graph and a tree.

type Vertex = usize;
type Distance = usize;
type Edge = (Vertex, Vertex, Distance);

#[derive(Debug,Copy,Clone)]
struct Outedge {
    vertex: Vertex,
    length: Distance,
}

type AdjacencyList = Vec<Outedge>;

// We're updating this struct to include parent and rank
#[derive(Debug)]
struct Graph {
    n: usize,
    outedges: Vec<Edge>,  // list of edges
    parent: Vec<Vertex>,  // parent[i] is the parent ID of node i
    rank: Vec<usize>,     // how deep is the tree rooted at this node?
}

impl Graph {
    fn create_undirected(n:usize, outedges:Vec<Edge>) -> Graph {
        // Create a graph from a list of edges
        //
        // This function creates a graph from a list of edges and initializes
        // the parent and rank vectors.  It also sorts the edges by distance.
        // Internally, the graph is represented as a list of edges, a parent
        // vector, and a rank vector, with parents and ranks indexed in the
        // same order as the outedges vector.
        //
        // Arguments:
        //     n: number of nodes
        //     outedges: list of edges
        // Returns:
        //     Graph: a graph with the given number of nodes and edges

        // Initialize parent and rank vectors
        let parent: Vec<Vertex> = vec![];
        let rank: Vec<usize> = vec![];

        // Create the graph
        let mut g = Graph{n,outedges,parent,rank};

        // Sort the edges by distance  O(n log n)
        g.outedges.sort_by(|a, b| a.2.cmp(&b.2));

        // Initialize parent and rank vectors
        // From a tree perspective, it's just a forest of single node "trees"
        for node in 0..g.n {
            // The parent and rank vectors are indexed in the same order
            // as the outedges vector
            g.parent.push(node);  // set each node to be its own parent
            g.rank.push(0);      // set the rank of each node to 0
        }
        g
    }
    
    fn find(&mut self, i:Vertex) -> Vertex {
        // Recursively find the root of the tree rooted at i.
        // O(log n) -- logarithmic time
        //
        // Arguments:
        //     i: node to find the root of
        // Returns:
        //     Vertex: the root of the tree rooted at i

        if self.parent[i] != i {
            self.parent[i] = self.find(self.parent[i]);
        }
        return self.parent[i];
    }

    fn union(&mut self, i:Vertex, j:Vertex) {
        // Union the trees rooted at i and j by making the root of the
        // smaller ranked tree a child of the root of the larger tree. 
        // O(1) -- constant time
        //
        // Arguments:
        //     i: node to union with
        //     j: node to union with

        if self.rank[i] < self.rank[j] {
            self.parent[i] = j;
        } else if self.rank[i] > self.rank[j] {
            self.parent[j] = i;
        } else {
            self.parent[j] = i;
            self.rank[i] += 1;
        }
    }
}

Let's consider the following graph.

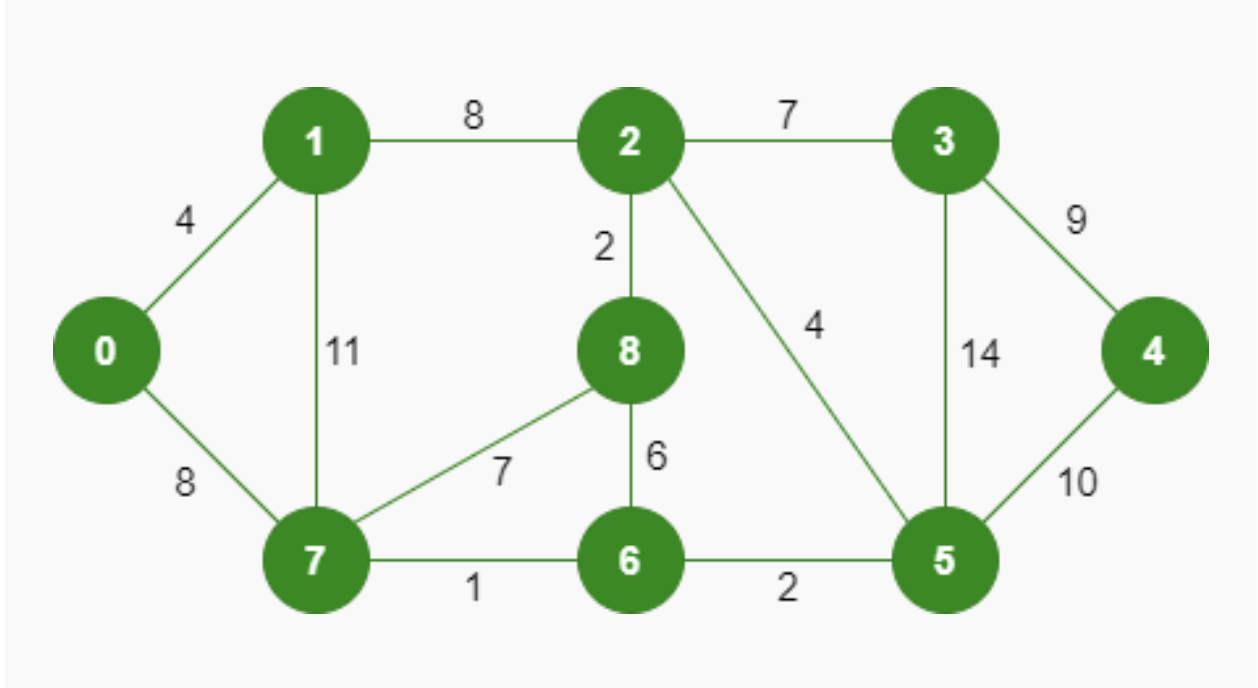
// Let's create the graph
let n = 9;
let edges: Vec<Edge> = vec![(7,6,1),(8,2,2),(6,5,2),(0,1,4),(2,5,4),(8,6,6),(2,3,7),(7,8,7),(0,7,8),(1,2,8),(3,4,9),(5,4,10),(1,7,11),(3,5,14)];
let mut g = Graph::create_undirected(n, edges);
g

Graph { n: 9, outedges: [(7, 6, 1), (8, 2, 2), (6, 5, 2), (0, 1, 4), (2, 5, 4), (8, 6, 6), (2, 3, 7), (7, 8, 7), (0, 7, 8), (1, 2, 8), (3, 4, 9), (5, 4, 10), (1, 7, 11), (3, 5, 14)], parent: [0, 1, 2, 3, 4, 5, 6, 7, 8], rank: [0, 0, 0, 0, 0, 0, 0, 0, 0] }

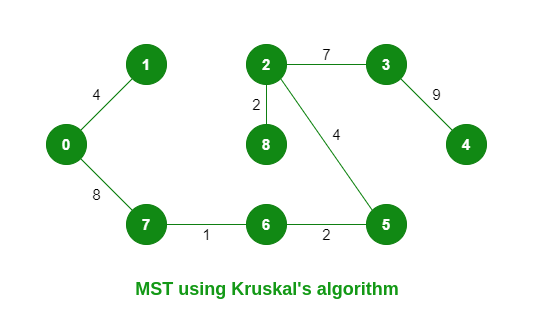
Kruskal's MST

impl Graph {
    fn KruskalMST(&mut self) -> Vec<Edge> {
        // Arguments:
        // self: a mutable reference to the graph
        // Returns:
        // Vec<Edge>: a vector of edges that form the minimum spanning tree

        // Initialize the result vector and counters
        let mut result: Vec<Edge> = vec![];
        let mut num_mst_e = 0;
        let mut next_edge = 0;  // start with the smallest weighted edge

        // Loop until we built a tree that has n-1 edges
        // A tree with n nodes has n-1 edges
        while num_mst_e < self.n - 1 {  // O(n)
            let (u,v,w) = self.outedges[next_edge];
            next_edge = next_edge + 1;

            let x = self.find(u);  // find the root of u
            let y = self.find(v);  // find the root of v
            
            // If u and v are in different trees, add the edge to the MST
            if x != y {
                num_mst_e += 1;
                result.push((u,v,w));
                self.union(x,y);  // join the two trees at their roots
            }
        }
        result
    }
}

Complexity Analysis

• while loop -- $n$ times
• Insde the loop
  • $\log n$ for each of 2 .find()
  • Constant time for the .union()

$$\approx n\times (2\log n+\mathrm{Constant})$$

Which, in order notation would be:

$$O(n\log n)$$

let result = g.KruskalMST();
let mut min_cost = 0;
for (u,v,w) in result {
    min_cost += w;
    println!("{} -- {} == {}", u, v, w)
}
println!("Spanning Tree Cost {}", min_cost);

7 -- 6 == 1
8 -- 2 == 2
6 -- 5 == 2
0 -- 1 == 4
2 -- 5 == 4
2 -- 3 == 7
0 -- 7 == 8
3 -- 4 == 9
Spanning Tree Cost 37

Other interesting graph problems (independent reading if you are interested)

• Matching: matching conference attendees to available desserts they like
  • Another formulation: maximum size set of independent edges in graph
  • Keep adding edges as long as you can
  • This will give factor 2 approximation

Traveling Salesman Approximation using MST

• Make a MST
• Pick an arbitrary vertex to be the root of the tree
• Run DFS from the root
• Shortcut where you can to shorten the tour.

For example a DFS of the above tree might yield:

0 - 1 - 0 - 7 - 6 - 5 - 2 - 8 - 2 - 3 - 4 - 3 - 2 - 5 - 6 - 7 - 0

Whenever you go to a new node through an already visited node, check to see if you can get there directly with less cost:

0 - 1 - (0) - 7 - 6 - 5 - 2 - 8 - 2 - 3 - 4 - (3 - 2) - 5 - 6 - 7 - 0

This is still not optimal but guaranteed to be within 2x of optimal (proof beyond our scope)

Greedy Algorithms Recap

• They often work well in practice
• They are polynomial on the size of their input (e.g. $n^2$ or better)
• They don't always find the best solutions (recall the coin problem with non-canonical denominations)
• They definitely don't prove that P != NP :-)

P vs NP

• P represents the class of problems that can be solved in polynomial time.

• NP represents the class of problems where solutions are unknown, but solutions can be verified in polynomial time

• If a problem is NP, is it also P?

• Answer this and get $1M

Technical Coding Challenge

Coding Challenge

Coding Challenge Review