Graph Exploration and Search Algorithms

About This Module

This module introduces fundamental graph exploration techniques, focusing on breadth-first search (BFS) and depth-first search (DFS). Students will learn to represent graphs using adjacency lists, implement graph data structures in Rust, and understand the theoretical foundations of graph traversal algorithms. The module provides essential building blocks for more advanced graph algorithms and demonstrates practical applications in data science and network analysis.

Prework

Before this lecture, please read:

• The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
• The Rust Book Chapter 10.1: "Generic Data Types" - https://doc.rust-lang.org/book/ch10-01-syntax.html
• Introduction to Algorithms Chapter 22: "Elementary Graph Algorithms" (if available, or similar graph theory resource)

Pre-lecture Reflections

1. What are the advantages and disadvantages of different graph representations (adjacency matrix vs. adjacency list)?
2. How do BFS and DFS differ in their exploration patterns and use cases?
3. What types of real-world problems can be modeled as graph traversal problems?

Lecture

Learning Objectives

By the end of this lecture, you should be able to:

• Represent graphs using adjacency lists in Rust
• Understand the difference between directed and undirected graphs
• Implement basic graph data structures with type aliases and structs
• Create utility functions for graph manipulation
• Identify appropriate graph representations for different problem types

Graph exploration overview

Graph exploration

Sample popular methods:

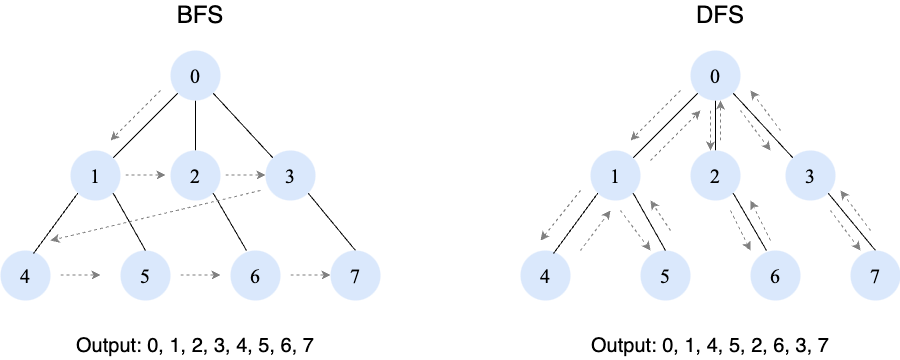
• breadth–first search (BFS)

  • uses a queue

• depth–first search (DFS)

  • uses a stack

• random walks

  • example: PageRank (see Homework 7)

BFS and DFS

Useful graph subroutines

We'll start by defining some useful routines.

// Define some datatype synonyms
type Vertex = usize;
type ListOfEdges = Vec<(Vertex,Vertex)>;
type AdjacencyLists = Vec<Vec<Vertex>>;

#[derive(Debug)]
struct Graph {
    n: usize, // vertex labels in {0,...,n-1}
    outedges: AdjacencyLists,
}

// reverse direction of edges on a list
fn reverse_edges(list:&ListOfEdges)
        -> ListOfEdges {
    let mut new_list = vec![];
    for (u,v) in list {
        new_list.push((*v,*u));
    }
    new_list
}

reverse_edges(&vec![(3,2),(1,1),(0,100),(100,0)])

[(2, 3), (1, 1), (100, 0), (0, 100)]

impl Graph {
    fn add_directed_edges(&mut self,
                          edges:&ListOfEdges) {
        for (u,v) in edges {
            self.outedges[*u].push(*v);
        }
    }
    fn sort_graph_lists(&mut self) {
        for l in self.outedges.iter_mut() {
            l.sort();
        }
    }
    fn create_directed(n:usize,edges:&ListOfEdges)
                                            -> Graph {
        let mut g = Graph{n,outedges:vec![vec![];n]};
        g.add_directed_edges(edges);
        g.sort_graph_lists();
        g                                        
    }
    
    fn create_undirected(n:usize,edges:&ListOfEdges)
                                            -> Graph {
        let mut g = Self::create_directed(n,edges);
        g.add_directed_edges(&reverse_edges(edges));
        g.sort_graph_lists();
        g                                        
    }
}