Hash Maps and Hash Sets: Key-Value Storage
About This Module
This module introduces HashMap and HashSet collections in Rust, which provide efficient key-value storage and set operations. You'll learn how to use these collections for fast lookups, counting, and deduplication tasks common in data processing.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 8.3: Storing Keys with Associated Values in Hash Maps
- (Optional)Additional reading about hash tables and their complexity Wikipedia: Hash table (intro only)
Pre-lecture Reflections -- Part 1
- Why must a
HashMaptake ownership of values likeString, and what memory safety problems does this solve? - How does the
entryAPI help you safely update a value? - The
getmethod returns anOption. Why is this a crucial design choice, and what common bugs does it prevent? - When would you choose to use a
HashMapover aVec, and what is the main performance trade-off for looking up data?
Pre-lecture Reflections -- Part 2
- How do hash maps achieve O(1) average-case lookup time?
- What are the tradeoffs between HashMap and BTreeMap in Rust?
- When would you use a HashSet vs a Vec
for storing unique values? - What makes a good hash function?
Learning Objectives
By the end of this module, you will be able to:
- Create and manipulate HashMap and HashSet collections
- Understand hash table operations and their complexity
- Choose appropriate collection types for different use cases
- Handle hash collisions and understand their implications
Hash maps
Collection HashMap<K,V>
Goal: a mapping from elements of K to elements of V
- elements of
Kcalled keys -- must be unique - elements of
Vcalled values -- need not be unique
Similar structure in other languages:
- Python: dictionaries
- C++:
unordered_map<K,V> - Java:
Hashtable<K,T>
Creating a HashMap
- Create a hash map and insert key-value pairs
- Extract a reference with
.get()
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); // Extracting a reference: returns `Option<&V>` println!("Boston University wins: {:?}", wins.get("Boston University")); println!("MIT wins: {:?}", wins.get("MIT")); }
Inserting a key-value pair if not present
To check if a key is present, and if not, insert a default value, you can use .entry().or_insert().
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); //Insert if not present, you can use `.entry().or_insert()`. wins.entry(String::from("MIT")).or_insert(10); println!("MIT wins: {:?}", wins.get("MIT")); }
Updating a value based on the old value
To update a value based on the old value, you can use .entry().or_insert()
and get a mutable reference to the value.
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); // Updating a value based on the old value: println!("Boston University wins: {:?}", wins.get("Boston University")); { // code block to limit how long the reference lasts let entry = wins.entry(String::from("Boston University")).or_insert(10); *entry += 50; } //wins.insert(String::from("Boston University"),24); println!("Boston University wins: {:?}", wins.get("Boston University")); }
Iterating
You can iterate over each key-value pair with a for loop similar to vectors.
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); for (k,v) in &wins { println!("{}: {}",k,v); }; println!("\nUse .iter(): "); for (k,v) in wins.iter() { println!("{}: {}",k,v); }; }
Iterating and Modifying Values
To modify values, you have to use mutable versions:
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); for (k,v) in &wins { println!("{}: {}",k,v); }; println!("\nUse implicit mutable iterator: "); for (k,v) in &mut wins { *v += 1; println!("{}: {}",k,v); }; println!("\nUse .iter_mut(): "); for (k,v) in wins.iter_mut() { *v += 1; println!("{}: {}",k,v); }; }
Using HashMaps with Match statements
- Let's use a hash map to store the price of different items in a cafe
#![allow(unused)] fn main() { use std::collections::HashMap; let mut crispy_crêpes_café = HashMap::new(); crispy_crêpes_café.insert(String::from("Nutella Crêpe"),5.85); crispy_crêpes_café.insert(String::from("Strawberries and Nutella Crêpe"),8.75); crispy_crêpes_café.insert(String::from("Roma Tomato, Pesto and Spinach Crêpe"),8.90); crispy_crêpes_café.insert(String::from("Three Mushroom Crêpe"),8.90); fn on_the_menu(cafe: &HashMap<String,f64>, s:String) { print!("{}: ",s); match cafe.get(&s) { // .get() returns an Option enum None => println!("not on the menu"), Some(price) => println!("${:.2}",price), } } on_the_menu(&crispy_crêpes_café, String::from("Four Mushroom Crêpe")); on_the_menu(&crispy_crêpes_café, String::from("Three Mushroom Crêpe")); }
Summary of Useful HashMap Methods
Basic Operations:
new(): Creates an empty HashMap.insert(key, value): Adds a key-value pair to the map. Returns true if the key was not present, false otherwise.remove(key): Removes a key-value pair from the map. Returns true if the key was present, false otherwise.get(key): Returns a reference to the value in the map, if any, that is equal to the given key.contains_key(key): Checks if the map contains a specific key. Returns true if present, false otherwise.len(): Returns the number of key-value pairs in the map.is_empty(): Checks if the map contains no key-value pairs.clear(): Removes all key-value pairs from the map.drain(): Returns an iterator that removes all key-value pairs and yields them. The map becomes empty after this operation.
Iterators and Views:
iter(): Returns an immutable iterator over the key-value pairs in the map.iter_mut(): Returns a mutable iterator over the key-value pairs in the map.keys(): Returns an iterator over the keys in the map.values(): Returns an iterator over the values in the map.values_mut(): Returns a mutable iterator over the values in the map.
See the documentation for more details.
How Hash Tables Work
Internal Representation
Array of Option
- A hash map is represented as an array of buckets, e.g. capacity
- The array is an array of
Option<T>enums likeVec<Option<T>>) , - And the
Some(<T>)variant has valueTwith tuple(key, value, hash) - So the internal representation is like
Vec<Option<(K, V, u64)>>
Hash function
- Use a hash function which is like a pseudorandom number generator with key as the seed, e.g.
- Pseudorandom means that the same key will always produce the same hash, but different keys will produce different hashes.
- Then take modulo of capacity , e.g.
index = hash % 8 = 6 - So ultimately maps keys into one of the buckets
Hash Function Examples
Let's calculate hash and index for different inputs using Rust's built-in hash function.
use std::collections::hash_map::DefaultHasher; use std::hash::{Hash, Hasher}; fn hash_function(input: &str) -> u64 { let mut hasher = DefaultHasher::new(); input.hash(&mut hasher); hasher.finish() } fn main() { let B = 8; // capacity of the hash map (e.g. number of buckets) let input = "Hello!"; let hash = hash_function(input); let index = hash % B; println!("Hash of '{}' is: {} and index is: {}", input, hash, index); let input = "Hello"; // slight change in input let hash = hash_function(input); let index = hash % B; println!("Hash of '{}' is: {} and index is: {}", input, hash, index); let input = "hello"; // slight change in input let hash = hash_function(input); let index = hash % B; println!("Hash of '{}' is: {} and index is: {}", input, hash, index); }
- Any collisions?
- Try increasing the capacity to 16 and see how the index changes.
More Hash Function Examples
- Keys don't have to be strings.
- They can be any type that implements the
Hashtrait.
use std::collections::hash_map::DefaultHasher; use std::hash::{Hash, Hasher}; fn generic_hash_function<T: Hash>(input: &T) -> u64 { let mut hasher = DefaultHasher::new(); input.hash(&mut hasher); hasher.finish() } fn main() { // Using the generic hash function with different types println!("\nUsing generic_hash_function:"); println!("String hash: {}", generic_hash_function(&"Hello, world!")); println!("Integer hash: {}", generic_hash_function(&42)); // println!("Float hash: {}", generic_hash_function(&3.14)); // what if we try float? println!("Bool hash: {}", generic_hash_function(&true)); println!("Tuple hash: {}", generic_hash_function(&(1, 2, 3))); println!("Vector hash: {}", generic_hash_function(&vec![1, 2, 3, 4, 5])); println!("Char hash: {}", generic_hash_function(&'A')); }
What if you try to hash a float?
General ideas
- Store keys (and associated values and hashes) in buckets
- Indexing: Use hash function to find bucket holding key and value.
Collision: two keys mapped to the same bucket
- Very unlikely given the pseudorandom nature of the hash function
- What to do if two keys in the same bucket
Handling collisions
Probing
- Each bucket entry: (key, value, hash)
- Use a deterministic algorithm to find an open bucket
Inserting:
- entry busy: try , , etc.
- insert into first empty
Searching:
- try , , , etc.
- stop when found or empty entry
Handling collisions, example
Step 1
Step 1: Empty hash map with 4 buckets
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | | empty | | empty |
+-------+ +-------+ +-------+ +-------+
Step 2
Step 2: Insert key="apple", hash("apple") = 42
hash("apple") = 42
42 % 4 = 2 ← insert at index 2
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | |apple,v| | empty |
| | | | | h=42 | | |
+-------+ +-------+ +-------+ +-------+
^
insert here
Step 3
Step 3: Insert key="banana", hash("banana") = 14
hash("banana") = 14
14 % 4 = 2 ← collision! index 2 is occupied, and not same key
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | |apple,v| | empty |
| | | | | h=42 | | |
+-------+ +-------+ +-------+ +-------+
^
occupied, check next
Step 4
Step 4: Linear probing - check next bucket (index 3)
Index 2 is full, try (2+1) % 4 = 3
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | |apple,v| |banana,v|
| | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
insert here
Step 5
Step 5: Insert key="cherry", hash("cherry") = 10
hash("cherry") = 10
10 % 4 = 2 ← collision again!
Check index 2: occupied (apple), not (cherry)
Check index 3: occupied (banana), not (cherry)
Check index 0: empty! ← wrap around and insert
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
insert here after wrapping around
Searching for a key
Current state of hash map:
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
Step 1
Step 1: Search for key="cherry"
hash("cherry") = 10
10 % 4 = 2 ← start searching at index 2
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
check here first
Step 2
Step 2: Check index 2
Index 2: key = "apple" ≠ "cherry"
bucket occupied, continue probing
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
not found, try next
Step 3
Step 3: Check index 3 (next probe)
Index 3: key = "banana" ≠ "cherry"
bucket occupied, continue probing
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
not found, try next
Step 4
Step 4: Check index 0 (wrap around)
Index 0: key = "cherry" = "cherry" ✓
FOUND! Return value
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
FOUND: return value v
Key point: Linear probing continues until we either:
- Find a matching key (success)
- Find an empty bucket (key doesn't exist)
- Check all buckets (hash map is full)
What is worse case scenario?
-
All keys map to the same bucket.
-
We have to check all buckets to find the key.
-
This is time complexity.
-
This is the worst case scenario for linear probing.
What is the average case scenario?
-
Each bucket has 1 key.
-
We have to check about 1 bucket to find the key.
-
This is time complexity.
-
This is the average case scenario for linear probing.
Growing the collection: amortization
Keep track of the number of filled entries.
When the number of keys
- Double
- Pick new hash function
- Move the information
Adversarial data
-
Could create lots of collisions
-
Potential basis for denial of service attacks
What makes a good hash function?
- Uniform distribution of inputs to the buckets available!!!
- Consistent hashing adds the property that not too many things move around when the number of buckets changes
http://www.partow.net/programming/hashfunctions/index.html
https://en.wikipedia.org/wiki/Consistent_hashing
https://doc.rust-lang.org/std/collections/struct.HashMap.html
To Dig Deeper (Optional)
Clone, inspect and debug/single-step through a simple implementation that supports creation, insert, get and remove.
See how index is found from hashing the key.
See how collision is handled.
Hashing with custom types in Rust
How do we use custom datatypes as keys?
Required for hashing:
- check if
Kequal - compute a hash function for elements of
K
#![allow(unused)] fn main() { use std::collections::HashMap; struct Point { x:i64, y:i64, } let point = Point{x:2,y:-1}; let mut elevation = HashMap::new(); elevation.insert(point,2.3); }
Most importantly:
[E0277] Error: the trait bound `Point: Eq` is not satisfied
[E0277] Error: the trait bound `Point: Hash` is not satisfied
Required traits for custom types
In order for a data structure to work as a key for hashmap, they need three traits:
PartialEq(required byEq)- ✅ Symmetry: If a == b, then b == a.
- ✅ Transitivity: If a == b and b == c, then a == c.
- ❌ Reflexivity is NOT guaranteed (because e.g. NaN != NaN in floats).
Eq- ✅ Reflexivity: a == a is always true.
- ✅ Symmetry: If a == b, then b == a.
- ✅ Transitivity: If a == b and b == c, then a == c.
Hash- Supports deterministic output of a hash function
- Consistency with Equality -- if two values are equal , then their hashes are equal
- Non-Invertibility -- One way. You cannot reconstruct the original value from the hash
- etc...
Default implementation
EqandPartialEqare automatically derived for most types.
#![allow(unused)] fn main() { use std::collections::HashMap; #[derive(Debug,Hash,Eq,PartialEq)] struct DistanceKM(u64); let mut tired = HashMap::new(); tired.insert(DistanceKM(30),true); println!("{:?}", tired); }
Reminder: All the traits that you can automatically derive from
- Clone: Allow user to make an explicit copy
- Copy: Allow user to make an implicit copy
- Debug: Allow user to print contents
- Default: Allow user to initialize with default values (Default::default())
- Hash: Allow user to use it as a key to a hash map or set.
- Eq: Allow user to test for equality
- Ord: Allow user to sort and fully order types
- PartialEq: Obeys most rules for equality but not all
- PartialOrd: Obeys most rules for ordering but not all
Using Floats as Keys
Note: You can use this for HW7.
Use ordered_float crate to get a type that implements Eq and Hash.
A wrapper around floats providing implementations of Eq, Ord, and Hash.
NaN is sorted as greater than all other values and equal to itself, in contradiction with the IEEE standard.
use ordered_float::OrderedFloat;
use std::f32::NAN;
use std::collections::{HashMap, HashSet};
fn main() {
let mut v = [OrderedFloat(NAN), OrderedFloat(2.0), OrderedFloat(1.0)];
v.sort();
assert_eq!(v, [OrderedFloat(1.0), OrderedFloat(2.0), OrderedFloat(NAN)]);
let mut m: HashMap<OrderedFloat<f32>, String> = HashMap::new();
m.insert(OrderedFloat(3.14159), "pi".to_string());
assert!(m.contains_key(&OrderedFloat(3.14159)));
let mut s: HashSet<OrderedFloat<f32>> = HashSet::new();
s.insert(OrderedFloat(3.14159));
assert!(s.contains(&OrderedFloat(3.14159)));Using Floats as Keys (Alternative)
Not all basic types support the Eq and Hash traits (f32 and f64 do not). The reasons have to do with the NaN and Infinity problems we discussed last time.
- If you find yourself needing floats as keys consider converting the float to a collection of integers
- Floating point representation consists of Sign, Exponent and Mantissa, each integer
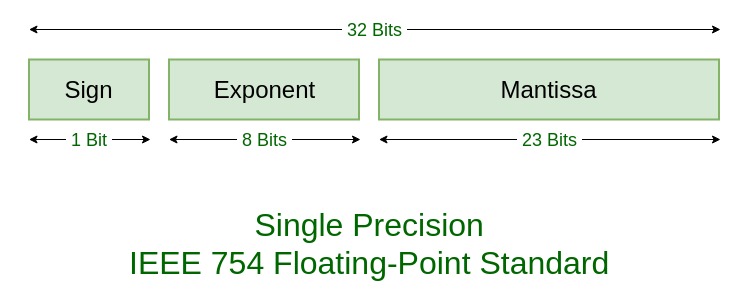
float_num = (-1)^sign * mantissa * 2^exponent where
signis -1 or 1mantissaisu23between 0 and 2^23exponentisi8between -127 and 128
// Built-in Rust library for traits on numbers
cargo add num-traits
#![allow(unused)] fn main() { let num:f64 = 3.14159; // Some float println!("num: {:32.21}", num); }
Question: Why is the number printed different than the number assigned?
Answer: Floating point can't exactly represent every decimal number. See above.
Let's decompose the floating point number into its components:
use num_traits::Float;
let num:f64 = 3.14159; // Some float
println!("num: {:32.21}", num);
let base:f64 = 2.0;
// Deconstruct the floating point
let (mantissa, exponent, sign) = Float::integer_decode(num);
println!("mantissa: {} exponent: {} sign: {}", mantissa, exponent, sign);
// Conver to f64
let sign_f:f64 = sign as f64;
let mantissa_f:f64 = mantissa as f64;
let exponent_f:f64 = base.powf(exponent as f64);
// Recalculate the floating point value
let new_num:f64 = sign_f * mantissa_f * exponent_f;
println!("{:32.31} {:32.31}", num, new_num);mantissa: 7074231776675438 exponent: -51 sign: 1
3.1415899999999998826183400524314 3.1415899999999998826183400524314
Let's check it:
#![allow(unused)] fn main() { let mantissa:u64 = 7074231776675438; let exponent:i8 = -51; let sign:i8 = 1; let base:f64 = 2.0; //convert to f64 let sign_f:f64 = sign as f64; let mantissa_f:f64 = mantissa as f64; let exponent_f:f64 = base.powf(exponent as f64); // Recalculate the floating point value let new_num:f64 = sign_f * mantissa_f * exponent_f; println!("{:32.31}", new_num); }
HashSet<K>
"A HashMap without values"
- No value associated with keys
- Just a set of items
- Same implementation
- Fastest way to do membership tests and some set operations
Creating a HashSet
- Create:
HashSet::new() .insert(),.is_empty(),.contains()
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); println!("Is empty: {}", covid.is_empty()); // insert values for i in 2019..=2022 { covid.insert(i); }; println!("Is empty: {}", covid.is_empty()); println!("Contains 2019: {}", covid.contains(&2019)); println!("Contains 2015: {}", covid.contains(&2015)); }
Growing the collection: amortization
- Let's monitor the length and capacity as we insert values.
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); println!("Length: {}, Capacity: {}", covid.len(), covid.capacity()); println!("Is empty: {}", covid.is_empty()); // insert values for i in 2019..=2022 { covid.insert(i); println!("Length: {}, Capacity: {}", covid.len(), covid.capacity()); }; println!("Length: {}, Capacity: {}", covid.len(), covid.capacity()); println!("Is empty: {}", covid.is_empty()); }
- More expensive than growing a
Vecbecause we need to rehash all the elements.
Iterating over a HashSet
You can iterate over a HashSet with a for loop.
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); // insert values for i in 2019..=2022 { covid.insert(i); }; // use the implicit iterator for year in &covid { print!("{} ",year); } println!(); // use the explicit iterator for year in covid.iter() { print!("{} ",year); } println!(); }
Question: Why aren't the years in the order we inserted them?
Using .get() and .insert()
We can use .get() and .insert(), similarly to how we used them in HashMaps.
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); // insert values for i in 2019..=2022 { covid.insert(i); }; // Returns `None` if not in the HashSet println!("{:?}", covid.get(&2015)); println!("{:?}", covid.get(&2021)); covid.insert(2015); // insert 2015 if not present covid.insert(2020); // insert 2020 if not present // iterate over the set for year in &covid { print!("{} ",year); } }
Summary of Useful HashSet Methods
Basic Operations:
new(): Creates an empty HashSet.insert(value): Adds a value to the set. Returns true if the value was not present, false otherwise.remove(value): Removes a value from the set. Returns true if the value was present, false otherwise.contains(value): Checks if the set contains a specific value. Returns true if present, false otherwise.len(): Returns the number of elements in the set.is_empty(): Checks if the set contains no elements.clear(): Removes all elements from the set.drain(): Returns an iterator that removes all elements and yields them. The set becomes empty after this operation.
Set Operations:
union(&self, other: &HashSet<T>): Returns an iterator over the elements that are in self or other (or both).intersection(&self, other: &HashSet<T>): Returns an iterator over the elements that are in both self and other.difference(&self, other: &HashSet<T>): Returns an iterator over the elements that are in self but not in other.symmetric_difference(&self, other: &HashSet<T>): Returns an iterator over the elements that are in self or other, but not in both.is_subset(&self, other: &HashSet<T>): Checks if self is a subset of other.is_superset(&self, other: &HashSet<T>): Checks if self is a superset of other.is_disjoint(&self, other: &HashSet<T>): Checks if self has no elements in common with other.
Iterators and Views:
iter(): Returns an immutable iterator over the elements in the set.get(value): Returns a reference to the value in the set, if any, that is equal to the given value.
See the documentation for more details.
In-Class Exercise 1: Word Frequency Counter
Task: Create a HashMap that counts the frequency of each word in the following sentence:
"rust is awesome rust is fast rust is safe"Your code should:
- Split the sentence into words. (Hint: Use
.split_whitespace()on your string and iterate over the result.) - Count how many times each word appears using a HashMap
- Print each word and its frequency
Hint: Use .entry().or_insert() to initialize or increment counts.
Expected Output:
rust: 3
is: 3
awesome: 1
fast: 1
safe: 1
Solution
use std::collections::HashMap; fn main() { let sentence = "rust is awesome rust is fast rust is safe"; let mut word_count = HashMap::new(); for word in sentence.split_whitespace() { let count = word_count.entry(word).or_insert(0); *count += 1; } for (word, count) in &word_count { println!("{}: {}", word, count); } }
In-Class Exercise 2: Programming Languages Analysis
Task: Two developers list their known programming languages. Create two HashSets and perform set operations to analyze their skills.
Developer 1 knows: Rust, Python, JavaScript, C++, Go
Developer 2 knows: Python, Java, JavaScript, Ruby, Go
Your code should find and print:
- Languages both developers know (intersection)
- Languages unique to Developer 1 (difference)
- All languages known by at least one developer (union)
- Languages known by exactly one developer (symmetric difference)
Hint: Create two HashSets and use set operations methods shown earlier.
Solutions will be added here after class.
Solution
use std::collections::HashSet; fn main() { // Insert one at a time let mut dev1 = HashSet::new(); dev1.insert("Rust"); dev1.insert("Python"); dev1.insert("JavaScript"); dev1.insert("C++"); dev1.insert("Go"); // Iterate over a vector and insert let mut dev2 = HashSet::new(); let dev2_languages = vec!["Python", "Java", "JavaScript", "Ruby", "Go"]; for lang in dev2_languages { dev2.insert(lang); } println!("Languages both know:"); for lang in dev1.intersection(&dev2) { println!(" {}", lang); } println!("\nLanguages unique to Developer 1:"); for lang in dev1.difference(&dev2) { println!(" {}", lang); } println!("\nAll languages known:"); for lang in dev1.union(&dev2) { println!(" {}", lang); } println!("\nLanguages known by exactly one:"); for lang in dev1.symmetric_difference(&dev2) { println!(" {}", lang); } }