Connected Components and Strongly Connected Components

About This Module

This module explores connected components in undirected graphs and strongly connected components in directed graphs. Students will learn advanced applications of DFS, including the two-pass algorithm for finding strongly connected components (Kosaraju's algorithm). The module covers both theoretical concepts and practical implementations, with applications to network analysis and graph decomposition problems.

Prework

Before this lecture, please read:

• Introduction to Algorithms Chapter 22.5: "Strongly connected components" (if available)
• The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
• Graph Theory reference on strongly connected components (any introductory graph theory text)

Pre-lecture Reflections

1. What is the difference between connected components and strongly connected components?
2. Why do we need different algorithms for directed vs. undirected graphs?
3. How might strongly connected components be useful in analyzing real-world networks?

Lecture

Learning Objectives

By the end of this lecture, you should be able to:

• Understand the difference between connected and strongly connected components
• Implement connected component detection using both BFS and DFS
• Apply Kosaraju's algorithm to find strongly connected components
• Analyze the computational complexity of component detection algorithms
• Apply component analysis to real-world graph problems

Connected components via DFS

Recursive DFS exploration: walk all connected vertices depth-first rather than breadth-first

fn mark_component_dfs(vertex:Vertex, graph:&Graph, component:&mut Vec<Option<Component>>, component_no:Component) {
    component[vertex] = Some(component_no);
    for w in graph.outedges[vertex].iter() {
        if let None = component[*w] {
            mark_component_dfs(*w,graph,component,component_no);
        }        
    }
}

Going over all components and assigning vertices:

let n: usize = 9;
let edges: Vec<(Vertex,Vertex)> = vec![(0,1),(0,2),(1,2),(2,4),(0,4),(5,7),(6,8)];
let graph = Graph::create_undirected(n, &edges);

let mut component = vec![None;graph.n];
let mut component_count = 0;

for v in 0..graph.n {
    if let None = component[v] {
        component_count += 1;
        mark_component_dfs(v,&graph,&mut component,component_count);
    }
};

Connected components via DFS

Let's verify the results:

print!("{} components:\n[  ",component_count);
for v in 0..n {
    print!("{}:{}  ",v,component[v].unwrap());
}
println!("]\n");

4 components:
[  0:1  1:1  2:1  3:2  4:1  5:3  6:4  7:3  8:4  ]

Takeaway: Works just as well as BFS for finding connected components.

BFS vs. DFS

Both have complexity of $O(V+E)$

BFS

• gives graph distances between vertices (fundamental problem!)
• connectivity

DFS

• What is it good for?

Lots of things!

Examples:

• find edges/vertices crucial for connectivity
• orient edges of a graph so it is still connected
• strongly connected components in directed graphs
• Traversal of trees (inorder, preorder, postorder)
• Topological Sorting (Scheduling)
• Matching people and jobs

Topological sort (pseudocode for home study)

Represents an order of the nodes that respects dependencies from directed graphs.

Assume this is a graph of dependent tasks.

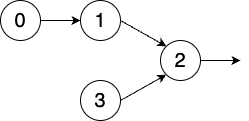
Used whenever you have to schedule work only after satisfying dependencies.

Used in Neural Network Backpropagation.

Valid topo sorts:

• 0, 1, 3, 2
• 0, 3, 1, 2
• 3, 0, 1, 2

Invalid topo sorts:

• 0, 1, 2, 3
• 1, 3, 0, 2
• ...

Pseudocode (For study at home)

Every node can have one of three marks:

• unmarked: initial state
• temporary mark: being processed
• permanent mark: fully processed

In the beginngin all nodes are unmarked.

Pick an unmarked node and call visit() on that node.

L ← Empty list that will contain a valid order of nodes
while exists nodes without a permanent mark do
    select an unmarked node n
    visit(n)

function visit(node n)
    if n has a permanent mark then
        return
    if n has a temporary mark then
        stop   (graph has at least one cycle -- can't be sorted)

    mark n with a temporary mark

    for each node m with an edge from n to m do
        visit(m)

    remove temporary mark from n
    mark n with a permanent mark
    add n to head of L

Complexith of topological sort

Complexity is $O(V+E)$. Just doing a DFS.

Strongly connected components (for directed graphs)

Only applies to directed graphs.

Strong connectivity

Strongly connected component:

A maximal set of vertices such that you can get from any of them to any other one. So like connected components but taking directionality into account

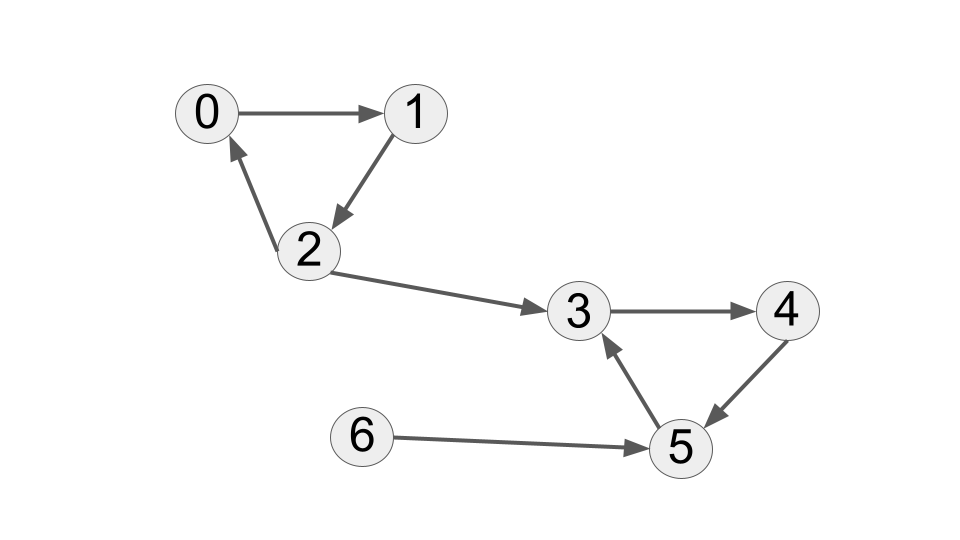
Strongly connected: nodes 0, 1, 2

Strongly connected: nodes, 3, 4, 5

Find the unique decomposition via two DFS runs

General idea

First DFS:

• maintain auxiliary stack $S$
• visit all vertices, starting DFS multiple times from unvisited vertices as needed
• put each vertex, when done going over its neighbors, on the stack

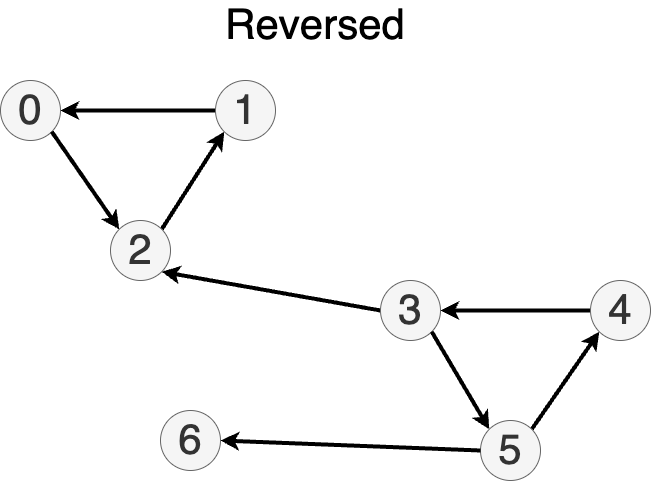
Second DFS:

• reverse edges of the graph!!!
• consider vertices in order from the stack
• for each unvisited vertex, start DFS: it will visit a new strongly connected component

Implementation

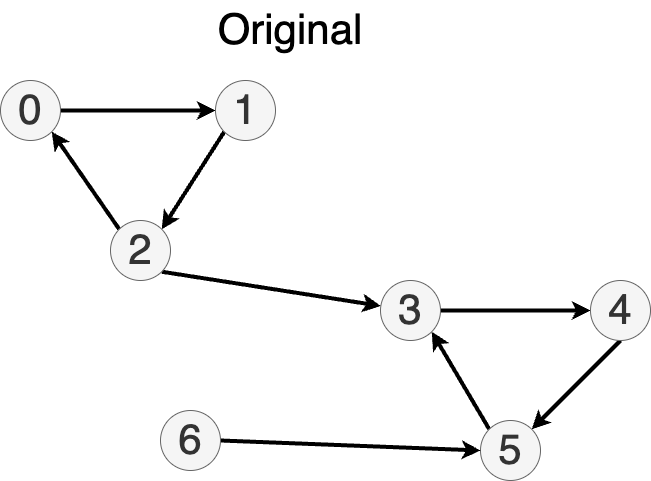
let n: usize = 7;
let edges: ListOfEdges = vec![(0,1),(1,2),(2,0),(3,4),(4,5),(5,3),(2,3),(6,5)];
let graph = Graph::create_directed(n, &edges);
let graph_reverse = Graph::create_directed(n,&reverse_edges(&edges));
println!("{:?}\n{:?}",graph,graph_reverse);

Graph { n: 7, outedges: [[1], [2], [0, 3], [4], [5], [3], [5]] }
Graph { n: 7, outedges: [[2], [0], [1], [2, 5], [3], [4, 6], []] }

Implementation (first DFS)

let mut stack: Vec<Vertex> = Vec::new();
let mut visited = vec![false;graph.n];

// push vertex onto stack after all descendents are processed (a.k.a. finishing times)
fn dfs_collect_stack(v:Vertex, graph:&Graph, stack:&mut Vec<Vertex>, visited:&mut Vec<bool>) {
    if !visited[v] {
        visited[v] = true;
        for w in graph.outedges[v].iter() {
            dfs_collect_stack(*w, graph, stack, visited);
        }
        stack.push(v);
        println!("pushed {}", v);
    }
}

for v in 0..graph.n {
    dfs_collect_stack(v,&graph,&mut stack,&mut visited);
};
stack

pushed 5
pushed 4
pushed 3
pushed 2
pushed 1
pushed 0
pushed 6




[5, 4, 3, 2, 1, 0, 6]

Implementation (second DFS, reversed graph)

let mut component: Vec<Option<Component>> = vec![None;graph.n];
let mut component_count = 0;

while let Some(v) = stack.pop() {
    if let None = component[v] {
        component_count += 1;
        mark_component_dfs(v, &graph_reverse, &mut component, component_count);
    }
};

print!("{} components:\n",component_count);
for c in 1..=component_count {
    print!("Component {}: ", c);
    for v in 0..n {
       if component[v].unwrap() == c {
          print!("{} ",v);
       }
    }
    println!();
}
println!();

3 components:
Component 1: 6 
Component 2: 0 1 2 
Component 3: 3 4 5 

Rust project version

Rust project version in strongly_connected folder in case you want to debug and inspect.