Overview
This course builds on DS110 (Python for Data Science) by expanding on programming language, systems, and algorithmic concepts introduced in the prior course. The course begins by exploring the different types of programming languages and introducing students to important systems level concepts such as computer architecture, compilers, file systems, and using the command line. It then moves to introducing a high performance language (Rust) and how to use it to implement a number of fundamental CS data structures and algorithms (lists, queues, trees, graphs etc). Then it covers how to use Rust in conjunction with external libraries to perform data manipulation and analysis.
Prerequisites: CDS 110 or equivalent
A1 Course Staff
Section A1 Instructor: Thomas Gardos
Email: tgardos@bu.edu
Office hours: Tuesdays, 3:30-4:45pm @ CCDS 1623
If you want to meet but cannot make office hours, send a private note on Piazza with at least 2 suggestions for times that you are available, and we will find a time to meet.
A1 TAs
-
Zach Gentile
- Email: zgentile@bu.edu
- Office Hours: Mondays, 1:30-3:30pm
- Location: CDS 15th Floor (Office Hours Area)
-
Emir Tali
- Email: etali@bu.edu
- Office Hours: Wednesdays, 11:30am - 1:30pm
A1 CAs
-
Ting-Hung Jen
- Email: allen027@bu.edu
- Office Hours: Fridays 3:30-5:30
- Location: CDS 15th Floor (Office Hours Area)
-
Matt Morris
- Email: mattmorr@bu.edu
- Office Hours: Mon/Wed 12:15-1:15
B1 Course Staff
Section B1 Instructor: Lauren Wheelock
Email: laurenbw@bu.edu
Office hours: Wed 2:30-4:00 @ CCDS 1506
Coffee slots: Fri 2:30-3:30 @ CCDS 1506
If you want to meet but cannot make office hours, send a private note on Piazza with at least 2 suggestions for times that you are available, and we will find a time to meet.
B1 Teaching Assistant
- TA: Joey Russoniello
- Email: jmrusso@bu.edu
- Office Hours: Thursdays, 10am-12 noon
- Location: CDS 15th Floor (Office Hours Area)
B1 Course Assistants |
-
Ava Yip
- Email: avayip@bu.edu
- Office Hours: Tuesdays 3:45-5:45
- Location: CDS 15th Floor (Office Hours Area)
-
Pratik Tribhuwan
- Email: pratikrt@bu.edu
- Office Hours: Fridays 12:00-2:00
- Location: CDS 15th Floor (Office Hours Area)
Lectures and Discussions
A1 Lecture: Tuesdays, Thursdays 2:00pm-3:15pm (LAW AUD)
Section A Discussions (Wednesdays, 50 min):
- A2: 12:20pm – 1:10pm, CDS B62, (led by Zach) Note new location!!
- A3: 1:25pm – 2:15pm, IEC B10, (led by Zach)
- A4: 2:30pm – 3:20pm CGS 311, (led by Emir)
- A5: 3:35pm – 4:25pm CGS 315, (led by Emir)
B1 Lecture: Mondays, Wednesdays, Fridays 12:20pm-1:10pm (WED 130)
Section B Discussions (Fridays, 50 min):
- B2: Tue 11:00am – 11:50 (listed 12:15pm), 111 Cummington St MCS B37 (led by Joey)
- B3: Tue 12:30pm – 1:20 (listed 1:45pm), 3 Cummington Mall PRB 148 (led by Joey)
B4: Tue 2:00pm – 2:50pm (listed 3:15pm), 665 Comm Ave CDS 164B5: Tue 3:30pm – 4:20 (listed 4:45pm), 111 Cummington St MCS B31
Note: Discussion sections B4 and B5 are cancelled because of low enrollment. Please re-enroll in B2 or B3 if you were previously enrolled in B4 or B5.
Note: There are two sections of this course, they cover the same material and share a piazza and course staff but the discussion sections and grading portals are different. These are not interchangeable, you must attend the lecture and discussion sessions for your section!
Course Websites
-
Piazza
- Lecture Recordings
- Announcements and additional information
- Questions and discussions
-
Course Notes (https://ds210-fa25-private.github.io/):
- Syllabus (this document)
- Interactive lecture notes
-
Gradescope
- Homework, project, project proposal submissions
- Gradebook
-
GitHub Classroom: URL TBD
Course Content Overview
- Part 1: Foundations (command line, git) & Rust Basics (Weeks 1-3)
- Part 2: Core Rust Concepts & Data Structures (Weeks 4-5)
- Midterm 1 (~Week 5)
- Part 3: Advanced Rust & Algorithms (Weeks 6-10)
- Midterm 2 (~Week 10)
- Part 4: Data Structures and Algorithms (~Weeks 11-12)
- Part 5: Data Science & Rust in Practice (~Weeks 13-14)
- Final exam during exam week
For a complete list of modules and topics that will be kept up-to-date as we go through the term, see Lecture Schedule (MWF) and Lecture Schedule (TTH).
Course Format
Lectures will involve extensive hands-on practice. Each class includes:
- Interactive presentations of new concepts
- Small-group exercises and problem-solving activities
- Discussion and Q&A
Because of this active format, regular attendance and participation is important and counts for a significant portion of your grade (15%).
Discussions will review lecture material, provide homework support, and will adapt over the semester to the needs of the class. We will not take attendance but our TAs make this a great resource!
Pre-work will be assigned before most lectures to prepare you for in-class activities. These typically include readings plus a short ungraded quiz. We will also periodically ask for feedback and reflections on the course between lectures.
Homeworks will be assigned roughly weekly at first, and there will be longer two-week assignments later, reflecting the growing complexity of the material.
Exams Two midterms and a cumulative final exam covering theory and short hand-coding problems (which we will practice in class!)
The course emphasizes learning through practice, with opportunities for corrections and growth after receiving feedback on assignments and exams.
Course Policies
Grading Calculations
Your grade will be determined as:
- 15% homeworks (~9 assignments)
- 20% midterm 1
- 20% midterm 2
- 25% final exam
- 15% in-class activities
- 5% pre-work and surveys
I will use the standard map from numeric grades to letter grades (>=93 is A, >=90 is A-, etc). For the midterm and final, we may add a fixed number of "free" points to everyone uniformly to effectively curve the exam at our discretion - this will never result in a lower grade for anyone.
We will use gradescope to track grades over the course of the semester, which you can verify at any time and use to compute your current grade in the course for yourself.
Homeworks
Homework assignments will be submitted by uploading them to GitHub Classroom. Since it may be possible to rely on genAI tools to do these assignments, against the course policy, our grading emphasizes development process and coding best practices in addition to technical correctness.
Typically, 1/3 of the homework score will be for correctness (computed by automated tests for coding assignments), 1/3 for documenting of your process (sufficient commit history and comments), and 1/3 for communication and best practices, which can be attained by replying to and incorporating feedback given by the CAs and TAs on your work.
Exams
The final will be during exam week, date and location TBD. The two midterms will be in class during normal lecture time.
If you have a valid conflict with a test date, you must tell me as soon as you are aware, and with a minimum of one week notice (unless there are extenuating circumstances) so we can arrange a make-up test.
If you need accommodations for exams, schedule them with the Testing Center as soon as exam dates are firm. See below for more about accommodations.
Deadlines and late work
Homeworks will be due on the date specified in gradescope/github classroom.
If your work is up to 48-hours late, you can still qualify for up to 80% credit for the assignment. After 48 hours, late work will not be accepted unless you have made prior arrangements due to extraordinary circumstances.
Collaboration
You are free to discuss problems and approaches with other students but must do your own writeup. If a significant portion of your solution is derived from someone else's work (your classmate, a website, a book, etc), you must cite that source in your writeup. You will not be penalized for using outside sources as long as you cite them appropriately.
You must also understand your solution well enough to be able to explain it if asked.
Academic honesty
You must adhere to BU's Academic Conduct Code at all times. Please be sure to read it here. In particular: cheating on an exam, passing off another student's work as your own, or plagiarism of writing or code are grounds for a grade reduction in the course and referral to BU's Academic Conduct Committee. If you have any questions about the policy, please send me a private Piazza note immediately, before taking an action that might be a violation.
AI use policy
You are allowed to use GenAI (e.g., ChatGPT, GitHub Copilot, etc) to help you understand concepts, debug your code, or generate ideas. You should understand that this may may help or impede your learning depending on how you use it.
If you use GenAI for an assignment, you must cite what you used and how you used it (for brainstorming, autocomplete, generating comments, fixing specific bugs, etc.). You must understand the solution well enough to explain it during a small group or discussion in class.
Your professor and TAs/CAs are happy to help you write and debug your own code during office hours, but we will not help you understand or debug code that generated by AI.
For more information see the CDS policy on GenAI.
Attendance and participation
Since a large component of your learning will come from in-class activities and discussions, attendance and participation are essential and account for 15% of your grade.
Attendance will be taken in lecture through Piazza polls which will open at various points during the lecture. Understanding that illness and conflicts arise, up to 4 absences are considered excused and will not affect your attendance grade.
In most lectures, there will be time for small-group exercises, either on paper or using github. To receive participation credit on these occasions, you must identify yourself on paper or in the repo along with a submission. These submissions will not be graded for accuracy, just for good-faith effort.
Occasionally, I may ask for volunteers, or I may call randomly upon students or groups to answer questions or present problems during class. You will be credited for participation.
Absences
This course follows BU's policy on religious observance. Otherwise, it is generally expected that students attend lectures and discussion sections. If you cannot attend classes for a while, please let me know as soon as possible. If you miss a lecture, please review the lecture notes and lecture recording. If I cannot teach in person, I will send a Piazza announcement with instructions.
Accommodations
If you need accommodations, let me know as soon as possible. You have the right to have your needs met, and the sooner you let me know, the sooner I can make arrangements to support you.
This course follows all BU policies regarding accommodations for students with documented disabilities. If you are a student with a disability or believe you might have a disability that requires accommodations, please contact the Office for Disability Services (ODS) at (617) 353-3658 or access@bu.edu to coordinate accommodation requests.
If you require accommodations for exams, please schedule that at the BU testing center as soon as the exam date is set.
Re-grading
You have the right to request a re-grade of any homework or test. All regrade requests must be submitted using the Gradescope interface. If you request a re-grade for a portion of an assignment, then we may review the entire assignment, not just the part in question. This may potentially result in a lower grade.
Corrections
You are welcome to submit corrections on homework assignments or the midterms. This is an opportunity to take the feedback you have received, reflect on it, and then demonstrate growth. Corrections involve submitting an updated version of the assignment or test alongside the following reflections:
- A clear explanation of the mistake
- What misconception(s) led to it
- An explanation of the correction
- What you now understand that you didn't before
After receiving grades back, you will have one week to submit corrections. You can only submit corrections on a good faith attempt at the initial submission (not to make up for a missed assignment).
Satisfying this criteria completely for any particular problem will earn you back 50% of the points you originally lost (no partial credit).
Oral re-exams (Section B only)
In Section B, we will provide you with a topic breakdown of your midterm exams into a few major topics. After receiving your midterm grade, you may choose to do an oral re-exam on one of the topics you struggled with by scheduling an appointment with Prof. Wheelock. This will involve a short (~10 minute) oral exam where you will be asked to explain concepts and write code on a whiteboard. This score will replace your original score on the topic, with a cap of 90% on that topic.
T-TH Lecture Schedule
Note: Schedule will be frequently updated. Check back often.
Note: Homeworks will be distributed via Gradescope and GitHub Classroom. We'll also post notices on Piazza.
See also Module Topics by Week below.
Lecture Schedule
| Date | Lecture | Homework |
|---|---|---|
| Week 1 | --- | --- |
| Sep 2 | Lecture 1: Course Overview, Why Rust | |
| Sep 4 | Lecture 2: Hello Shell | |
| Week 2 | --- | --- |
| Sep 8 | HW1 Released | |
| Sep 9 | Lecture 3: Hello Git | |
| Sep 11 | Lecture 4: Hello Rust | |
| Week 3 | --- | --- |
| Sep 15 | HW1 Due | |
| Sep 16 | Lecture 5: Programming Languages, Guessing Game Part 1 | |
| Sep 18 | Lecture 6: Hello VSCode and GitHub Classroom | |
| Week 4 | --- | --- |
| Sep 23 | Lecture 7: Vars and Types, | |
| Sep 25 | Lecture 8: Finish Vars and Types, Cond Expressions, Functions, | |
| Week 5 | --- | --- |
| Sep 30 | Lecture 9: Finish Functions, Loops Arrays, Tuples | |
| Oct 2 | Lecture 10: Enum and Match | |
| Week 6 | --- | --- |
| Oct 7 | Lecture 11: A1 Midterm 1 Review | |
| Oct 9 | 🧐📚 Midterm 1 📚🧐 | |
| Week 7 | --- | --- |
| Oct 14 | No Class -- Monday Schedule | |
| Oct 16 | Lecture 12: Structs, Method Syntax, Methods Revisited | |
| Week 8 | --- | --- |
| Oct 21 | Lecture 13: Ownership and Borrowing, Strings and Vecs | |
| Oct 23 | Lecture 14: Slices, Modules, | |
| Week 9 | --- | --- |
| Oct 28 | Lecture 15: Crates, Rust Projects,Tests, Generics | |
| Oct 30 | Lecture 16: Generics, Traits | |
| Week 10 | --- | --- |
| Nov 4 | Lecture 17: Lifetimes, Closures | |
| Nov 6 | Lecture 18: , Iterators, Iters Closures | |
| Week 11 | --- | --- |
| Nov 11 | Lecture 19 -- Midterm 2 Review | |
| Nov 13 | 🧐📚 Midterm 2 📚🧐 | |
| Week 12 | --- | --- |
| Nov 18 | Lecture 20: Complexity Analysis, Hash Maps (only) | |
| Nov 20 | Lecture 21: Hashing Functions, Hash Sets, linked lists, | |
| Week 13 | --- | --- |
| Nov 25 | Lecture 22: Stacks, Queues | |
| Nov 27 | 🦃 No Class -- Thanksgiving Recess 🌽 | |
| Week 14 | --- | --- |
| Dec 2 | Lecture 23: Collections Deep Dive, | |
| Dec 3 | Exam 2 Corrections Due, 11:59pm | |
| Dec 4 | Lecture 24: Algorithms and Data Science | |
| Dec 8 | HW 7 Due, 11:59pm | |
| Week 15 | --- | --- |
| Dec 9 | Final Review | |
| Dec 10 | 🎉 Last Day of Classes 🎉 | |
| Dec 16 | 🧐📚 Final Exam 3:00pm -- 5:00pm 📚🧐 | Law Auditorium |
Module Topics by Week
Module topics by week for the Tues-Thurs A1 Section.
Work in progress. Check back often.
- Course overview
- Why Rust
- Hello Shell
- Hello Git
- Hello Rust
- Prog Languages
- Guessing Game Part 1
- Systems
- Hello VSCode
- Vars, types
- cond expr
- Functions
- loops
- derive debug
- Tuples
- enums, match
- Stack, heap, vec
- datatype sizes
- Ownership and borrowing
- cloning and copying
- Slices
- strings
- error handling
- Best practices, formatting, comments
(Midterm 1 -- Systems, Basic Rust)
- Modules, crates, Rust projects, (58, 60, 62, 64)
- File IO, Error handling (64, 100)
- Structs, methods (30, 31, 38)
- Generics, traits (42, 44)
- Collections, vectors, lifetimes (46, 92)
- Iterators and closures (94, 96, 98)
- Hashmaps, hashsets (52)
- Tests (48)
- Complexity analysis (50)
(Midterm 2 -- Advanced Rust)
- Calling Rust from Python (920)
- SWE project management / project intro (new, 900)
- Linked lists, stacks, queues (66, 68, 70)
- Graph representation / graph algo (54, 56)
- Graph search, BFS, DFS, CC/SCC (72, 74, 76, 78) - maybe not from scratch
- Priority queues, binary heap, sorting (82, 84) - maybe not from scratch
- Shortest path / trees part 2 (86)
- Algorithms (108, 110, 112)
- Divide and conquer / merge sort (122)
- NDArray, survey of data science in Rust (114, 120)
- More data science
- Parallel code (126)
(Final Exam)
MWF Lecture, HW, and Exam Schedule
See the B1 Schedule for an up-to-date schedule for the MWF (B1) section
DS210 Course Overview
About This Module
This module introduces DS-210: Programming for Data Science, covering course logistics, academic policies, grading structure, and foundational concepts needed for the course.
Overview
This course builds on DS110 (Python for Data Science). That, or an equivalent is a prerequisite.
We will cover
- programming languages
- computing systems concepts
- shell commands
And then spend the bulk of the course learning Rust, a modern, high-performance and more secure programming language.
Time permitting we dive into some common data structures and data science related libraries.
New This Semester
We've made some significant changes to the course based on observations and course evaluations.
Question: What have you heard about the course? Is it easy? Hard?
Changes include:
- Moving course notes from Jupyter notebooks to Rust
mdbook- This is the same format used by the Rust language book
- Addition of in-class group activites for almost every lecture where you
can reinforce what you learned and practice for exams
- Less lecture content, slowing down the pace
- Homeworks that progressively build on the lecture material and better match exam questions (e.g. 10-15 line code solutions)
- Elimination of course final project and bigger emphasis on in-class activities and participation.
- ...
Teaching Staff and Contact Information
Section A Instructor: Thomas Gardos
- Email: tgardos@bu.edu
- Office hours: Tuesdays, 3:30-4:45pm @ CCDS 1623
Section B Instructor: Lauren Wheelock
- Email: laurenbw@bu.edu
- Office hours: Wednesday, 2:30-4:00pm @ CCDS 1506
| Teaching Assistants | Course Assistants |
|---|---|
| TA: Zach Gentile Email: Office Hours: Mondays, 1:20-3:20pm | CA: Ting-Hung Jen Email: |
| TA: Joey Russoniello Email: Office Hours: Thursdays, 10am-12 noon | CA: Matt Morris Email: |
| TA: Emir Tali Email: Office Hours: Wednesdays, 11:30am - 1:30pm | CA: Pratik Tribhuwan Email: |
| CA: Ava Yip Email: |
Course Logistics
Lectures:
(A) Tue / Thu 2:00pm - 3:15pm, 765 Commonwealth Ave LAW AUD (B) Mon / Wed / Fri 12:20pm - 1:10pm, 2 Silber Way WED 130
Lectures and Discussions
A1 Lecture: Tuesdays, Thursdays 2:00pm-3:15pm (LAW AUD)
Section A Discussions (Wednesdays, 50 min): Led by TAs
A2: 12:20pm – 1:10pm, SAR 300, (Zach)
A3: 1:25pm – 2:15pm, IEC B10, (Zach)
A4: 2:30pm – 3:20pm CGS 311, (Emir)
A5: 3:35pm – 4:25pm CGS 315, (Emir)
B1 Lecture: Mondays, Wednesdays, Fridays 12:20pm-1:10pm (WED 130)
Section B Discussions (Fridays, 50 min??): Led by TAs
(listed as 75 minutes for technical reasons but actually meet for 50)
- B2: Tue 11:00am – 10:50 (listed 12:15pm), 111 Cummington St MCS B37 (Joey)
- B3: Tue 12:30pm – 1:20 (listed 1:45pm), 3 Cummington Mall PRB 148 (Joey)
B4: Tue 2:00pm – 2:50pm (listed 3:15pm), 665 Comm Ave CDS 164B5: Tue 3:30pm – 4:20 (listed 4:45pm), 111 Cummington St MCS B31
Note: Discussion sections B4 and B5 are cancelled because of low enrollment. Please re-enroll in B2 or B3 if you were previously enrolled in B4 or B5.
Course Websites
See welcome email for Piazza and Gradescope URLs.
-
Piazza:
- Lecture Notes
- Announcements and additional information
- Questions and discussions
-
Gradescope:
- Homework
- Gradebook
-
GitHub Classroom: URL TBD
Course objectives
This course teaches systems programming and data structures through Rust, emphasizing safety, speed, and concurrency. By the end, you will:
- Master key data structures and algorithms for CS and data science
- Understand memory management, ownership, and performance optimization
- Apply computational thinking to real problems using graphs and data science
- Develop Rust skills that transfer to other languages
Why are we learning Rust?
- Learning a second programming language builds CS fundamentals and teaches you to acquire new languages throughout your career
- Systems programming knowledge helps you understand software-hardware interaction and write efficient, low-level code
We're using Rust specifically because:
- Memory safety without garbage collection lets you see how data structures work in memory (without C/C++ headaches)
- Strong type system catches errors at compile time, helping you write correct code upfront
- Growing adoption in data science and scientific computing across major companies and agencies
More shortly.
Course Timeline and Milestones
- Part 1: Foundations (command line, git) & Rust Basics (Weeks 1-3)
- Part 2: Core Rust Concepts & Data Structures (Weeks 4-5)
- Midterm 1 (~Week 5)
- Part 3: Advanced Rust & Algorithms (Weeks 6-10)
- Midterm 2 (~Week 10)
- Part 4: Data Structures and Algorithms (~Weeks 11-12)
- Part 5: Data Science & Rust in Practice (~Weeks 13-14)
- Final exam during exam week
Course Format
Lectures will involve extensive hands-on practice. Each class includes:
- Interactive presentations of new concepts
- Small-group exercises and problem-solving activities
- Discussion and Q&A
Because of this active format, regular attendance and participation is important and counts for a significant portion of your grade (15%).
Discussions will review and reinforce lecture material through and provide further opportunities for hands-on practice.
Pre-work will be assigned before most lectures to prepare you for in-class activities. These typically include readings plus a short ungraded quiz. The quizz questions will reappear in the lecture for participation credit.
Homeworks will be assigned roughly weekly before the midterm, and there will be 2-3 longer two-week assigments after the deadline, reflecting the growing complexity of the material.
Exams 2 midterms and a cumulative final exam covering theory and short hand-coding problems (which we will practice in class!)
The course emphasizes learning through practice, with opportunities for corrections and growth after receiving feedback on assignments and exams.
In-class Activities
Syllabus Review Activity (20 min)
In groups of 2-3, review the course syllabus and answer the following questions:
Concrete:
- Add your names to a shared worksheet
- How are assignments and projects submitted?
- What happens if you submit work a day late?
- If you get stuck on an assignment and your friend explains how to do it, what should you do?
- What would it take to get full credit for attendance and participation?
- If you have accomodations for exams, how soon should you request them?
- When and how long are discussion sections?
Open-ended:
- What parts of the course policies seem standard and what parts seem unique?
- Identify 2-3 things in the syllabus that concern you
- What strategies could you use to address these concerns?
- Identify 2-3 things you're glad to see
- When do you plan to submit your first assignment / project? What do you think it will cover?
- List three questions about the course that aren't answered in the syllabus
AI use discussion (20 min)
Think-pair-share style, each ~6-7 minutes, with wrap-up.
See Gradescope assignment. Forms teams of 3.
Round 1: Learning Impact
"How might GenAI tools help your learning in this course? How might they get in the way?"
Round 2: Values & Fairness
"What expectations do you have for how other students in this course will or won't use GenAI? What expectations do you have for the teaching team so we can assess your learning fairly given easy access to these tools?"
Round 3: Real Decisions
"Picture yourself stuck on a challenging Rust problem at midnight with a deadline looming. What options do you have? What would help you make decisions you'd feel good about?"
More course policies
See syllabus for more information on:
- deadlines and late work
- collaboration
- academic honesty
- AI use policy (discussed below)
- Attendance and participation
- Absences
- Accommodations
- Regrading
- Corrections
AI use policy
You are allowed to use GenAI (e.g., ChatGPT, GitHub Copilot, etc) to help you understand concepts, debug your code, or generate ideas.
You should understand that this may may help or impede your learning depending on how you use it.
If you use GenAI for an assignment, you must cite what you used and how you used it (for brainstorming, autocomplete, generating comments, fixing specific bugs, etc.).
You must understand the solution well enough to explain it during a small group or discussion in class.
Your professor and TAs/CAs are happy to help you write and debug your own code during office hours, but we will not help you understand or debug code that is generated by AI.
For more information see the CDS policy on GenAI.
Intro surveys
Please fill out the intro survey posted on Gradescope.
Why Rust?
Why Systems Programming Languages Matter
Importance of Systems Languages:
- Essential for building operating systems, databases, and infrastructure
- Provide fine-grained control over system resources
- Enable optimization for performance-critical applications
- Foundation for higher-level languages and frameworks
Performance Advantages:
- Generally compiled languages like Rust are needed to scale to large, efficient deployments
- Can be 10x to 100x faster than equivalent Python code
- Better memory management and resource utilization
- Reduced runtime overhead compared to interpreted languages
Memory Safety: A Critical Advantage
What is Memory Safety?
Memory safety prevents common programming errors that can lead to security vulnerabilities:
- Buffer overflows
- Use-after-free errors
- Memory leaks
- Null pointer dereferences
Industry Recognition:
Major technology companies and government agencies are actively moving to memory-safe languages:
- Google, Microsoft, Meta have efforts underway to move infrastructure code from C/C++ to Rust
- U.S. Government agencies recommend memory-safe languages for critical infrastructure
- DARPA has programs focused on translating C to Rust
- CISA (Cybersecurity and Infrastructure Security Agency) advocates for memory-safe roadmaps
 CISA -- The case for memory safe roadmaps
CISA -- Cybersecurity and Infrastructure Security Agency
CISA -- The case for memory safe roadmaps
CISA -- Cybersecurity and Infrastructure Security Agency
Programming Paradigms: Interpreted vs. Compiled
Interpreted Languages (e.g., Python):
Advantages:
- Interactive development environment
- Quick iteration and testing
- Rich ecosystem for data science (Jupyter, numpy, pandas)
- Easy to learn and prototype with
Compiled Languages (e.g., Rust):
Advantages:
- Superior performance and efficiency
- Early error detection at compile time
- Optimized machine code generation
- Better for production systems
Development Process:
- Write a program
- Compile it (catch errors early)
- Run and debug optimized code
- Deploy efficient executables
Using Rust in a Jupyter Notebook
The project EvCxR (Evaluation Context for Rust) creates a Rust kernel that you can use in Jupyter notebooks.
- Can be helpful for interactive learning
- There are some quirks when creating Rust code cells in a notebook
- Variables and functions are kept in global state
- Order of cell execution matters!
- Previous versions of the course notes used this format
We use Rust mdbook with code cells that get executed on the
Rust playground.
Same format that the Rust language book is written.
Technical Coding Interviews
And finally...
If you are considering technical coding interviews, they sometimes ask you to solve problems in a language other than python.
Many of the in-class activities and early homework questions will be Leetcode/HackerRank style challenges.
This is good practice!
Hello Shell!
About This Module
This module introduces you to the command-line interface and essential shell commands that form the foundation of systems programming and software development. You'll learn to navigate the file system, manipulate files, and use the terminal effectively for Rust development.
Prework Readings
Review this module.
Pre-lecture Reflections
Before class, consider these questions:
- What advantages might a command-line interface offer over graphical interfaces? What types of tasks seem well-suited for command-line automation?
- How does the terminal relate to the development workflow you've seen in other programming courses?
Learning Objectives
By the end of this module, you should be able to:
- Create, copy, move, and delete files and directories at the command line
- Understand file permissions and ownership concepts
- Use pipes and redirection for basic text processing
- Set up an organized directory structure for programming projects
- Feel comfortable working in the terminal environment
Why the Command Line Matters
For Programming and Data Science:
# Quick file operations
ls *.rs # Find all Rust files
grep "TODO" src/*.rs # Search for TODO comments across files
wc -l data/*.csv # Count lines in all CSV files
Advantages over GUI:
- Speed: Much faster for repetitive tasks
- Precision: Exact control over file operations
- Automation: Commands can be scripted and repeated
- Remote work: Essential for server management
- Development workflow: Many programming tools use command-line interfaces
File Systems
File System Structure Essentials
A lot of DS and AI infrastructure runs on Linux/Unix type filesystems.
Root Directory (/):
The slash character represents the root of the entire file system.
Directory Conventions
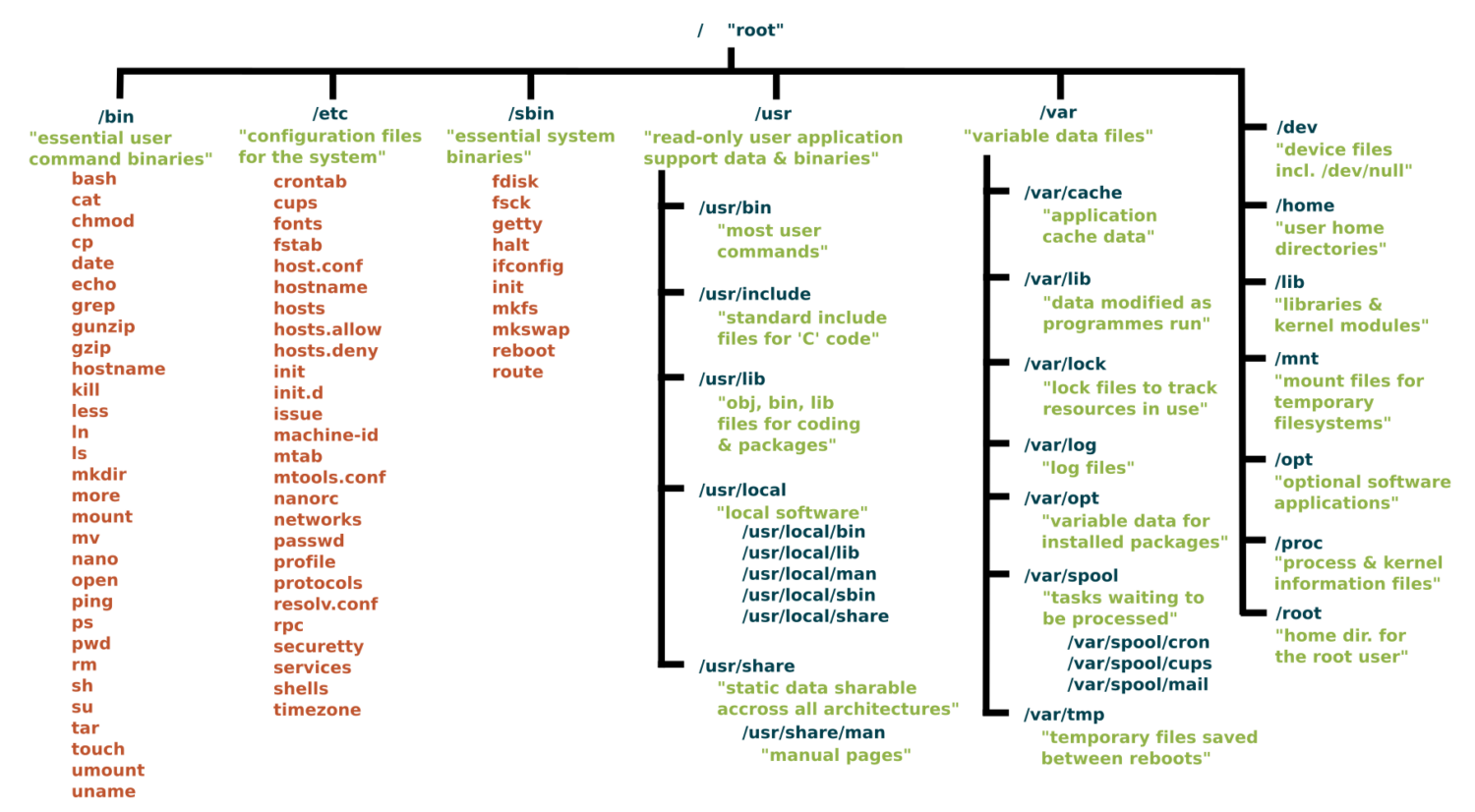
/: The slash character by itself is the root of the filesystem/bin: A place containing programs that you can run/boot: A place containing the kernel and other pieces that allow your computer to start/dev: A place containing special files representing all your devices/etc: A place with lots of configuration information (i.e. login and password data)/home: All user's home directories/lib: A place for all system libraries/mnt: A place to mount external file systems/opt: A place to install user software/proc: Lots of information about your computer and what is running on it/sbin: Similar to bin but for the superuser/usr: Honestly a mishmash of things and rather overlapping with other directories/tmp: A place for temporary files that will be wiped out on a reboot/var: A place where many programs write files to maintain state
Key Directories You'll Use:
/ # Root of entire system
├── home/ # User home directories
│ └── username/ # Your personal space
├── usr/ # User programs and libraries
│ ├── bin/ # User programs (like cargo, rustc)
│ └── local/ # Locally installed software
└── tmp/ # Temporary files
Navigation Shortcuts:
~= Your home directory.= Current directory..= Parent directory/= Root directory
To explore further
You can read more about the Unix filesystem at https://en.wikipedia.org/wiki/Unix_filesystem.
The Linux shell
It is an environment for finding files, executing programs, manipulating (create, edit, delete) files and easily stitching multiple commands together to do something more complex.
Windows and MacOS has command shells, but Windows is not fully compatible, however MacOS command shell is.
Windows Subystem for Linux is fully compatible.
In Class Activity Part 1: Access/Install Terminal Shell
Directions for MacOS Users and Windows Users.
macOS Users:
Your Mac already has a terminal! Here's how to access it:
-
Open Terminal:
- Press
Cmd + Spaceto open Spotlight - Type "Terminal" and press Enter
- Or: Applications → Utilities → Terminal
- Press
-
Check Your Shell:
echo $SHELL # Modern Macs use zsh, older ones use bash -
Optional: Install Better Tools:
Install Homebrew (package manager for macOS)
/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"
Install useful tools
brew install tree # Visual directory structure
brew install ripgrep # Fast text search
Windows Users:
Windows has several terminal options. For this exercise we recommend Option 1, Git bash.
When you have more time, you might want to explore Windows Subsystem for Linux so you can have a full, compliant linux system accessible on Windows.
PowerShell aliases some commands to be Linux-like, but they are fairly quirky.
We recommend Git Bash or WSL:
-
Option A: Git Bash (Easier)
- Download Git for Windows from git-scm.com
- During installation, select "Use Git and optional Unix tools from the Command Prompt"
- Open "Git Bash" from Start menu
- This gives you Unix-like commands on Windows
-
Option B: Windows Subsystem for Linux (WSL)
# Run PowerShell as Administrator, then: wsl --install # Restart your computer # Open "Ubuntu" from Start menu -
Option C: PowerShell (Built-in)
- Press
Win + Xand select "PowerShell" - Note: Commands differ from Unix (use
dirinstead ofls, etc.) - Not recommended for the in-class activities.
- Press
Verify Your Setup (Both Platforms)
pwd # Should show your current directory
ls # Should list files (macOS/Linux) or use 'dir' (PowerShell)
which ls # Should show path to ls command (if available)
echo "Hello!" # Should print Hello!
Essential Commands for Daily Use
Navigation and Exploration:
pwd # Show current directory path
ls # List files in current directory
ls -al # List files with details and hidden files
cd directory_name # Change to directory
cd .. # Go up one directory
cd ~ # Go to home directory
Creating and Organizing:
mkdir project_name # Create directory
mkdir -p path/to/dir # Create nested directories
touch filename.txt # Create empty file
cp file.txt backup.txt # Copy file
mv old_name new_name # Rename/move file
rm filename # Delete file
rm -r directory_name # Delete directory and contents
rm -rf directory_name # Delete dir and contents without confirmation
Viewing File Contents:
cat filename.txt # Display entire file
head filename.txt # Show first 10 lines
tail filename.txt # Show last 10 lines
less filename.txt # View file page by page (press q to quit)
File Permissions Made Simple
Understanding ls -l Output:
-rw-r--r-- 1 user group 1024 Jan 15 10:30 filename.txt
drwxr-xr-x 2 user group 4096 Jan 15 10:25 dirname
Permission Breakdown:
- First character:
-(file) ord(directory) - Next 9 characters in groups of 3:
- Owner permissions (rwx): read, write, execute
- Group permissions (r-x): read, no write, execute
- Others permissions (r--): read only
We will see these kinds of permissions again in Rust programming!
Common Permission Patterns:
644orrw-r--r--: Files you can edit, others can read755orrwxr-xr-x: Programs you can run, others can read/run600orrw-------: Private files only you can access
Pipes and Redirection Basics
Saving Output to Files:
ls > file_list.txt # Save directory listing to file
echo "Hello World" > notes.txt # Overwrite file contents
echo "It is me" >> notes.text # Append to file content
Combining Commands with Pipes:
ls | grep ".txt" # List only .txt files
cat file.txt | head -5 # Show first 5 lines of file
ls -l | wc -l # Count number of files in directory
Practical Examples:
# Find large files
ls -la | sort -k5 -nr | head -10
# Count total lines in all text files
cat *.txt | wc -l
# Search for pattern and save results
grep "error" log.txt > errors.txt
Setting Up for Programming
Creating Project Structure:
# Create organized development directory
# The '-p' means make intermediate directories as required
mkdir -p ~/development/rust_projects
mkdir -p ~/development/data_science
mkdir -p ~/development/tools
# Navigate to project area
cd ~/development/rust_projects
# Create specific project
mkdir my_first_rust_project
cd my_first_rust_project
Customizing Your Shell Profile (Optional)
Understanding Shell Configuration Files:
Your shell reads a configuration file when it starts up. This is where you can add aliases, modify your PATH, and customize your environment.
Common Configuration Files:
- macOS (zsh):
~/.zshrc - macOS (bash):
~/.bash_profileor~/.bashrc - Linux (bash):
~/.bashrc - Windows Git Bash:
~/.bash_profile
Finding Your Configuration File:
It's in your Home directory.
# Check which shell you're using (MacOS/Linus)
echo $SHELL
# macOS with zsh
echo $HOME/.zshrc
# macOS/Linux with bash
echo $HOME/.bash_profile
echo $HOME/.bashrc
Adding Useful Aliases:
# Edit your shell configuration file (choose the right one for your system)
nano ~/.zshrc # macOS zsh
nano ~/.bash_profile # macOS bash or Git Bash
nano ~/.bashrc # Linux bash
# Add these helpful aliases:
alias ll='ls -la'
alias ..='cd ..'
alias ...='cd ../..'
alias projects='cd ~/development'
alias rust-projects='cd ~/development/rust_projects'
alias grep='grep --color=auto'
alias tree='tree -C'
# Custom functions
# This will make a directory specified as the argument and change into it
mkcd() {
mkdir -p "$1" && cd "$1"
}
Modifying Your PATH:
# Add to your shell configuration file
export PATH="$HOME/bin:$PATH"
export PATH="$HOME/.cargo/bin:$PATH" # For Rust tools (we'll add this later)
# For development tools
export PATH="/usr/local/bin:$PATH"
Applying Changes:
# Method 1: Reload your shell configuration
source ~/.zshrc # For zsh
source ~/.bash_profile # For bash
# Method 2: Start a new terminal session
# Method 3: Run the command directly
exec $SHELL
Useful Environment Variables:
# Add to your shell configuration file
export EDITOR=nano # Set default text editor
export HISTSIZE=10000 # Remember more commands
export HISTFILESIZE=20000 # Store more history
# Color support for ls
export CLICOLOR=1 # macOS
export LS_COLORS='di=34:ln=35:so=32:pi=33:ex=31:bd=34:cd=34:su=0:sg=0:tw=34:ow=34' # Linux
Shell Configuration with Git Branch Name
A useful shell configuration is modify the shell command prompt to show your current working directory and your git branch name if you are in a git project.
See DS549 Shell Configuraiton for instructions.
Shell scripts
A way to write simple programs using the linux commands and some control flow elements. Good for small things. Never write anything complicated using shell.
Shell Script File
Shell script files typically use the extension *.sh, e.g. script.sh.
Shell script files start with a shebang line, #!/bin/bash.
#!/bin/bash
echo "Hello world!"
To execute shell script you can use the command:
source script.sh
Hint: You can use the
nanotext editor to edit simple files like this.
In-Class Activity: Shell Challenge
Prerequisite: You should have completed Part I above to have access to a Linux or MacOS style shell.
Part 2: Scavenger Hunt
Complete the steps using only the command line!
You can use echo to write to the file, or text editor nano.
Feel free to reference the cheat sheet below and the notes above.
-
Create a directory called
treasure_huntin your course projects folder. -
In that directory create a file called
command_line_scavenger_hunt.txtthat contains the following:- Your name / group members
-
Run these lines and record the output into that
.txtfile:
whoami # What's your username?
hostname # What's your computer's name?
pwd # Where do you start?
echo $HOME # What's your home directory path?
-
Inside that directory, create a text file named
clue_1.txtwith the content "The treasure is hidden in plain sight" -
Create a subdirectory called
secret_chamber -
In the
secret_chamberdirectory, create a file calledclue_2.txtwith the content "Look for a hidden file" -
Create a hidden file in the
secret_chamberdirectory called.treasure_map.txtwith the content "Congratulations. You found the treasure" -
When you're done, change to the parent directory of
treasure_huntand run the commandzip -r treasure_hunt.zip treasure_hunt.- Or if you are on Git Bash, you may have to use the command
tar.exe -a -c -f treasure_hunt.zip treasure_hunt
- Or if you are on Git Bash, you may have to use the command
-
Upload
treasure_hunt.zipto gradescope - next time we will introduce git and github and use that platform going forward. -
Optional: For Bragging Rights Create a shell script that does all of the above commands and upload that to Gradescope as well.
Command Line Cheat Sheet
Basic Navigation & Listing
Mac/Linux (Bash/Zsh):
# Navigate directories
cd ~ # Go to home directory
cd /path/to/directory # Go to specific directory
pwd # Show current directory
# List files and directories
ls # List files
ls -la # List all files (including hidden) with details
ls -lh # List with human-readable file sizes
ls -t # List sorted by modification time
Windows (PowerShell/Command Prompt):
# Navigate directories
cd ~ # Go to home directory (PowerShell)
cd %USERPROFILE% # Go to home directory (Command Prompt)
cd C:\path\to\directory # Go to specific directory
pwd # Show current directory (PowerShell)
cd # Show current directory (Command Prompt)
# List files and directories
ls # List files (PowerShell)
dir # List files (Command Prompt)
dir /a # List all files including hidden
Get-ChildItem -Force # List all files including hidden (PowerShell)
Finding Files
Mac/Linux:
# Find files by name
find /home -name "*.pdf" # Find all PDF files in /home
find . -type f -name "*.log" # Find log files in current directory
find /usr -type l # Find symbolic links
# Find files by other criteria
find . -type f -size +1M # Find files larger than 1MB
find . -mtime -7 # Find files modified in last 7 days
find . -maxdepth 3 -type d # Find directories up to 3 levels deep
Windows:
# PowerShell - Find files by name
Get-ChildItem -Path C:\Users -Filter "*.pdf" -Recurse
Get-ChildItem -Path . -Filter "*.log" -Recurse
dir *.pdf /s # Command Prompt - recursive search
# Find files by other criteria
Get-ChildItem -Recurse | Where-Object {$_.Length -gt 1MB} # Files > 1MB
Get-ChildItem -Recurse | Where-Object {$_.LastWriteTime -gt (Get-Date).AddDays(-7)} # Last 7 days
Counting & Statistics
Mac/Linux:
# Count files
find . -name "*.pdf" | wc -l # Count PDF files
ls -1 | wc -l # Count items in current directory
# File and directory sizes
du -sh ~/Documents # Total size of Documents directory
du -h --max-depth=1 /usr | sort -rh # Size of subdirectories, largest first
ls -lah # List files with sizes
Windows:
# Count files (PowerShell)
(Get-ChildItem -Filter "*.pdf" -Recurse).Count
(Get-ChildItem).Count # Count items in current directory
# File and directory sizes
Get-ChildItem -Recurse | Measure-Object -Property Length -Sum # Total size
dir | sort length -desc # Sort by size (Command Prompt)
Text Processing & Search
Mac/Linux:
# Search within files
grep -r "error" /var/log # Search for "error" recursively
grep -c "hello" file.txt # Count occurrences of "hello"
grep -n "pattern" file.txt # Show line numbers with matches
# Count lines, words, characters
wc -l file.txt # Count lines
wc -w file.txt # Count words
cat file.txt | grep "the" | wc -l # Count lines containing "the"
Windows:
# Search within files (PowerShell)
Select-String -Path "C:\logs\*" -Pattern "error" -Recurse
(Select-String -Path "file.txt" -Pattern "hello").Count
Get-Content file.txt | Select-String -Pattern "the" | Measure-Object
# Command Prompt
findstr /s "error" C:\logs\* # Search for "error" recursively
find /c "the" file.txt # Count occurrences of "the"
System Information
Mac/Linux:
# System stats
df -h # Disk space usage
free -h # Memory usage (Linux)
system_profiler SPHardwareDataType # Hardware info (Mac)
uptime # System uptime
who # Currently logged in users
# Process information
ps aux # List all processes
ps aux | grep chrome # Find processes containing "chrome"
ps aux | wc -l # Count total processes
Windows:
# System stats (PowerShell)
Get-WmiObject -Class Win32_LogicalDisk | Select-Object Size,FreeSpace
Get-WmiObject -Class Win32_ComputerSystem | Select-Object TotalPhysicalMemory
(Get-Date) - (Get-CimInstance Win32_OperatingSystem).LastBootUpTime # Uptime
Get-LocalUser # User accounts
# Process information
Get-Process # List all processes
Get-Process | Where-Object {$_.Name -like "*chrome*"} # Find chrome processes
(Get-Process).Count # Count total processes
# Command Prompt alternatives
wmic logicaldisk get size,freespace # Disk space
tasklist # List processes
tasklist | find "chrome" # Find chrome processes
File Permissions & Properties
Mac/Linux:
# File permissions and details
ls -l filename # Detailed file information
stat filename # Comprehensive file statistics
file filename # Determine file type
# Find files by permissions
find . -type f -readable # Find readable files
find . -type f ! -executable # Find non-executable files
Windows:
# File details (PowerShell)
Get-ItemProperty filename # Detailed file information
Get-Acl filename # File permissions
dir filename # Basic file info (Command Prompt)
# File attributes
Get-ChildItem | Where-Object {$_.Attributes -match "ReadOnly"} # Read-only files
Network & Hardware
Mac/Linux:
# Network information
ip addr show # Show network interfaces (Linux)
ifconfig # Network interfaces (Mac/older Linux)
networksetup -listallhardwareports # Network interfaces (Mac)
cat /proc/cpuinfo # CPU information (Linux)
system_profiler SPHardwareDataType # Hardware info (Mac)
Windows:
# Network information (PowerShell)
Get-NetAdapter # Network interfaces
ipconfig # IP configuration (Command Prompt)
Get-WmiObject Win32_Processor # CPU information
Get-ComputerInfo # Comprehensive system info
Platform-Specific Tips
Mac/Linux Users:
- Your home directory is
~or$HOME - Hidden files start with a dot (.)
- Use
man commandfor detailed help - Try
which commandto find where a command is located
Windows Users:
- Your home directory is
%USERPROFILE%(Command Prompt) or$env:USERPROFILE(PowerShell) - Hidden files have the hidden attribute (use
dir /ahto see them) - Use
Get-Help commandin PowerShell orhelp commandin Command Prompt for detailed help - Try
where commandto find where a command is located
Universal Tips:
- Use Tab completion to avoid typing long paths
- Most shells support command history (up arrow or Ctrl+R)
- Combine commands with pipes (
|) to chain operations - Search online for "[command name] [your OS]" for specific examples
Hello Git!
About This Module
This module introduces version control concepts and Git fundamentals for individual development workflow. You'll learn to track changes, create repositories, and use GitHub for backup and sharing. This foundation prepares you for collaborative programming and professional development practices.
Prework
Read through this module.
If you're on Windows, install git from
https://git-scm.com/downloads.
You probably already did this to use git-bash for the Shell class activity.
MacOS comes pre-installed with git.
From your Home or projects directory in a terminal or cmd, run the command:
git clone https://github.com/cdsds210/simple-repo.git
If it is the first time, it may ask you to login or authenticate.
Ultimately, you want to cache your GitHub credentials locally on your computer. This page gives instructions.
Optionally you can browse through these Git references:
- Git Handbook - Getting Started - Core concepts overview
- Pro Git Chapter 1: Getting Started - Version control basics
- GitHub Hello World Guide - GitHub workflow
- Review: Git Commands Cheat Sheet
Pre-lecture Reflections
Before class, consider these questions:
- Why is version control essential for any programming project?
- How does Git differ from simply making backup copies of files?
- What problems arise when multiple people work on the same code without version control?
- How might Git help you track your learning progress in this course?
- What's the difference between Git (the tool) and GitHub (the service)?
Learning Objectives
By the end of this module, you should be able to:
- Understand why version control is critical for programming
- Configure Git for first-time use
- Create repositories and make meaningful commits
- Connect local repositories to GitHub
- Use the basic Git workflow for individual projects
- Recover from common Git mistakes
You may want to follow along with the git commands in your own environment during the lecture.
Why Version Control Matters
The Problem Without Git:
my_project.rs
my_project_backup.rs
my_project_final.rs
my_project_final_REALLY_FINAL.rs
my_project_broken_trying_to_fix.rs
my_project_working_maybe.rs
The Solution With Git:
git log --oneline
a1b2c3d Fix input validation bug
e4f5g6h Add error handling for file operations
h7i8j9k Implement basic calculator functions
k1l2m3n Initial project setup
Key Benefits:
- Never lose work: Complete history of all changes
- Fearless experimentation: Try new ideas without breaking working code
- Clear progress tracking: See exactly what changed and when
- Professional workflow: Essential skill for any programming job
- Backup and sharing: Store code safely in the cloud
Core Git Concepts
Repository (Repo): A folder tracked by Git, containing your project and its complete history.
Commit: A snapshot of your project at a specific moment, with a message explaining what changed.
The Three States:
- Working Directory: Files you're currently editing
- Staging Area: Changes prepared for next commit
- Repository: Committed snapshots stored permanently
The Basic Workflow:
Edit files → Stage changes → Commit snapshot
(add) (commit)
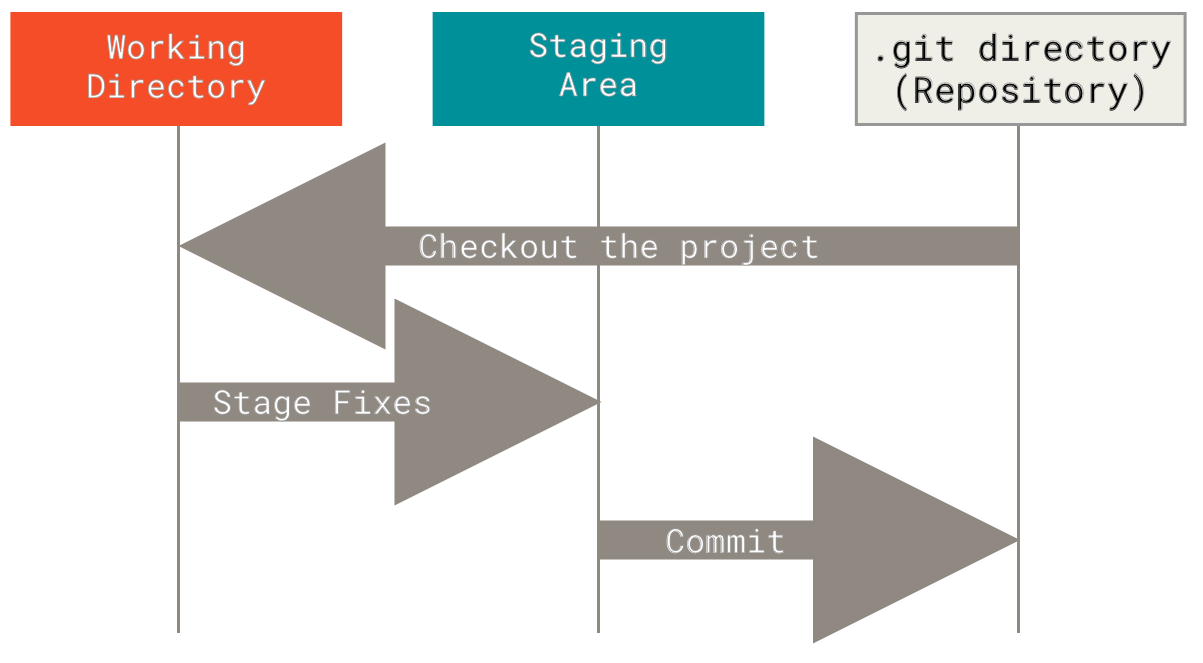
Push: Uploads your local commits to a remote repository (like GitHub). Takes your local changes and shares them with others.
Local commits → Push → Remote repository
Pull: Downloads commits from a remote repository and merges them into your current branch. Gets the latest changes from others.
Remote repository → Pull → Local repository (updated)
Merge: Combines changes from different branches. Takes commits from one branch and integrates them into another branch.
Feature branch + Main branch → Merge → Combined history
Pull Request (PR): A request to merge your changes into another branch, typically used for code review. You "request" that someone "pull" your changes into the main codebase.
Your branch → Pull Request → Review → Merge into main branch
Git Branching
Lightweight Branching:
Git's key strength is efficient branching and merging:
- Main branch: Usually called
main(ormasterin older repos) - Feature branches: Created for new features or bug fixes

Branching Benefits:
- Isolate experimental work
- Enable parallel development
- Facilitate code review process
- Support different release versions
Essential Git Commands
Here are some more of those useful shell commands!
One-Time Setup
# Configure your identity (use your real name and email)
git config --global user.name "Your Full Name"
git config --global user.email "your.email@example.com"
If you don't want to publish your email in all your commits on GitHub, then highly recommended to get a "no-reply" email address from GitHub. Here are directions.
# Set default branch name
git config --global init.defaultBranch main
Note: The community has moved away from
masteras the default branch name, but it may still be default in some installations.
# Verify configuration
git config --list
Starting a New Project
# Create project directory
mkdir my_rust_project
cd my_rust_project
# Initialize Git repository
git init
# Check status
git status
Daily Git Workflow (without GithHub)
# Create a descriptive branch name for the change you want to make
git checkout -b topic_branch
# Check what's changed
git status # See current state
git diff # See specific changes
# make edits to, for example filename.rs
# Stage changes for commit
git add filename.rs # Add specific file
git add . # Add all changes in current directory
# Create commit with a comment
git commit -m "Add calculator function"
# View history
git log # Full commit history
git log --oneline # Compact view
# View branches
git branch
# Switch back to main
git checkout main
# Merge topic branch back into main
git merge topic_branch
# Delete the topic branch when finished
git branch -d topic_branch
Writing Good Commit Messages
The Golden Rule: Your commit message should complete this sentence: "If applied, this commit will [your message here]"
Good Examples:
git commit -m "Add input validation for calculator"
git commit -m "Fix division by zero error"
git commit -m "Refactor string parsing for clarity"
git commit -m "Add tests for edge cases"
Bad Examples:
git commit -m "stuff" # Too vague
git commit -m "fixed it" # What did you fix?
git commit -m "more changes" # Not helpful
git commit -m "asdfjkl" # Meaningless
Commit Message Guidelines:
- Start with a verb: Add, Fix, Update, Remove, Refactor
- Be specific: What exactly did you change?
- Keep it under 50 characters for the first line
- Use present tense: "Add function" not "Added function"
Working with GitHub
Why GitHub?
- Remote backup: Your code is safe in the cloud
- Easy sharing: Share projects with instructors and peers
- Portfolio building: Showcase your work to employers
- Collaboration: Essential for team projects
Connecting to GitHub:
# Create repository on GitHub first (via web interface)
# Then connect your local repository:
git remote add origin https://github.com/yourusername/repository-name.git
git branch -M main
git push -u origin main
Note: The above instructions are provided to you by GitHub when you create an empty repository.
Git Remote Server (GitHub) Related Command
# Check remote connection
git remote -v
# Clone existing repository
git clone https://github.com/username/repository.git
cd repository
# Pull any changes from GitHub
git pull
# Push your commits to GitHub
git push
Daily GitHub Workflow
# Create a descriptive branch name for the change you want to make
git checkout -b topic_branch
# Check what's changed
git status # See current state
git diff # See specific changes
# make edits to, for example filename.rs
# Stage changes for commit
git add filename.rs # Add specific file
git add . # Add all changes in current directory
# Create commit with a comment
git commit -m "Add calculator function"
# View history
git log # Full commit history
git log --oneline # Compact view
# View branches
git branch
# Run local validation tests on changes
# Push to GitHub
git push origin topic_branch
# Create a Pull Request on GitHub
# Repeat above to make any changes from PR review comments
# When done, merge PR to main on GitHub
git checkout main
git pull
# Delete the topic branch when finished
git branch -d topic_branch
Git for Homework
Recommended Workflow:
# Start new assignment
cd ~/ds210/assignments
mkdir assignment_01
cd assignment_01
git init
# Make initial commit
touch README.md
echo "# Assignment 1" > README.md
git add README.md
git commit -m "Initial project setup for Assignment 1"
# Work and commit frequently
# ... write some code ...
git add src/main.rs
git commit -m "Implement basic data structure"
# ... write more code ...
git add src/main.rs
git commit -m "Add error handling"
# ... add tests ...
git add tests/
git commit -m "Add comprehensive tests"
# Final commit before submission
git add .
git commit -m "Final submission version"
Best Practices for This Course:
- Commit early and often: We expect to see a minimum of 3-5 commits per assignment
- One logical change per commit: Each commit should make sense on its own
- Meaningful progression: Your commit history should tell the story of your solution
- Clean final version: Make sure your final commit has working, clean code
Common Git Scenarios
"I made a mistake in my last commit message"
git commit --amend -m "Corrected commit message"
"I forgot to add a file to my last commit"
git add forgotten_file.rs
git commit --amend --no-edit
"I want to undo changes I haven't committed yet"
git checkout -- filename.rs # Undo changes to specific file
git reset --hard HEAD # Undo ALL uncommitted changes (CAREFUL!)
"I want to see what changed in a specific commit"
git show commit_hash # Show specific commit
git log --patch # Show all commits with changes
Understanding .gitignore
What NOT to Track: Some files should never be committed to Git:
# Rust build artifacts
/target/
Cargo.lock # Ignore for libraries, not applications
# IDE files
.vscode/settings.json
.idea/
*.swp
# OS files
.DS_Store
Thumbs.db
# Personal notes
notes.txt
TODO.md
Creating .gitignore:
# Create .gitignore file
touch .gitignore
# Edit with your preferred editor to add patterns above
# Commit the .gitignore file
git add .gitignore
git commit -m "Add .gitignore for Rust project"
Resources for learning more and practicing
- A gamified tutorial for the basics: https://ohmygit.org/
- Interactive online Git tutorial that goes a bit deper: https://learngitbranching.js.org/
- A downloadable app with tutorials and challenges: https://github.com/jlord/git-it-electron
- Another good tutorial (examples in ruby): https://gitimmersion.com/
- Pro Git book (free online): https://git-scm.com/book/en/v2
GitHub Collaboration Challenge
Form teams of three people.
Follow these instructions with your teammates to practice creating a GitHub repository, branching, pull requests (PRs), review, and merging. Work in groups of three—each person will create and review a pull request.
1. Create and clone the repository (≈3 min)
- Choose one teammate to act as the repository lead.
- They should log in to GitHub, click the “+” menu in the upper‑right and select New repository.
- Call the repository "github-class-challenge", optionally add a description, make the visibility public, check “Add a README,” and
- click Create repository.
- Go to Settings/Collaborators and add your teammates as developers with write access.
- Each team member needs a local copy of the repository. On the repo’s main page, click Code, copy the HTTPS URL, open a terminal, navigate to the folder where you want the project, and run:
git clone <repo‑URL>
Cloning creates a full local copy of all files and history.
2. Create your own topic branch (≈2 min)
A topic branch lets you make changes without affecting the default main branch. GitHub recommends using a topic branch when making a pull request.
On your local machine:
git checkout -b <your‑first‑name>-topic
git push -u origin <your‑first‑name>-topic # creates the branch on GitHub
Pick a branch name based on your first name (for example alex-topic).
3. Add a personal file, commit and push (≈5 min)
-
In your cloned repository (on your topic branch), create a new text file named after yourself—e.g.,
alex.txt. Write a few sentences about yourself (major, hometown, a fun fact). -
Stage and commit the file:
git add alex.txt git commit -m "Add personal bio"Good commit messages explain what changed.
-
Push your commit to GitHub:
git push
4. Create a pull request (PR) for your teammates to review (≈3 min)
- On GitHub, click Pull requests → New pull request.
- Set the base branch to
mainand the compare branch to your topic branch. - Provide a clear title (e.g. “Add Alex’s bio”) and a short description of what you added. Creating a pull request lets your collaborators review and discuss your changes before merging them.
- Request reviews from your two teammates.
5. Review your teammates’ pull requests (≈4 min)
- Open each of your teammates’ PRs.
- On the Conversation or Files changed tab, leave at least one constructive comment (ask a question or suggest something you’d like them to add). You can comment on a specific line or leave a general comment.
- Submit your review with the Comment option. Pull request reviews can be comments, approvals, or requests for changes; you’re only commenting at this stage.
6. Address feedback by making another commit (≈3 min)
-
Read the comments on your PR. Edit your text file locally in response to the feedback.
-
Stage, commit, and push the changes:
git add alex.txt git commit -m "Address feedback" git pushAny new commits you push will automatically update the open pull request.
-
Reply to the reviewer’s comment in the PR, explaining how you addressed their feedback.
7. Approve and merge pull requests (≈3 min)
- After each PR author has addressed the comments, revisit the PRs you reviewed.
- Click Review changes → Approve to approve the updated PR.
- Once a PR has at least one approval, a teammate other than the author should merge it.
-In the PR, scroll to the bottom and click Merge pull request, then Confirm merge. - Delete the topic branch when prompted; keeping the branch list tidy is good practice.
Each student should merge one of the other students’ PRs so everyone practices.
8. Capture a snapshot for submission (≈3 min)
- One teammate downloads a snapshot of the final repository. On the repo’s main page, click Code → Download ZIP. GitHub generates a snapshot of the current branch or commit.
- Open the Commits page (click the “n commits” link) and take a screenshot showing the commit history.
- Go to Pull requests → Closed, and capture a screenshot showing the three closed PRs and their approval status. You can also use the Activity view to see a detailed history of pushes, merges, and branch changes.
- Upload the ZIP file and screenshots to Gradescope.
Tips
- Use descriptive commit messages and branch names.
- Each commit is a snapshot; keep commits focused on a single change.
- Be polite and constructive in your feedback.
- Delete merged branches to keep your repository clean.
This exercise walks you through the entire GitHub flow—creating a repository, branching, committing, creating a PR, reviewing, addressing feedback, merging, and capturing a snapshot. Completing these steps will help you collaborate effectively on future projects.
Hello Rust!
About This Module
This module provides your first hands-on experience with Rust programming. You'll write actual programs, understand basic syntax, and see how Rust's compilation process works. We'll focus on building confidence through practical programming while comparing key concepts to Python.
Prework
Prework Readings
Review this module.
Read the following Rust basics:
- The Rust Programming Language - Chapter 1.2: Hello, World!
- The Rust Programming Language - Chapter 1.3: Hello, Cargo!
Optionally browse:
Pre-lecture Reflections
Before class, consider these questions:
- How does compiling code differ from running Python scripts directly?
- What might be the advantages of catching errors before your program runs?
- How does Rust's
println!macro compare to Python'sprint()function? - Why might explicit type declarations help prevent bugs?
- What challenges might you face transitioning from Python's flexibility to Rust's strictness?
Topics
- Installing Rust
- Compiled vs Interpretted Languages
- Write and compile our first simple program
Installing Rust
Before we can write Rust programs, we need to install Rust on your system.
From https://www.rust-lang.org/tools/install:
On MacOS:
# Install Rust via rustup
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
Question: can you interpret the shell command above?
On Windows:
Download and run rustup-init.exe (64-bit).
It will ask you some questions.
Download Visual Studio Community Edition Installer.
Open up Visual Studio Community Edition Installer and install the C++ core
desktop features.
Verify Installation
From MacOS terminal or Windows CMD or PowerShell
rustc --version # Should show Rust compiler version
cargo --version # Should show Cargo package manager version
rustup --version # Should show Rustup toolchain installer version
Troubleshooting Installation:
# Update Rust if already installed
rustup update
# Check which toolchain is active
rustup show
# Reinstall if needed (a last resort!!)
rustup self uninstall
# Then reinstall following installation steps above
Write and compile simple Rust program
Generally you would create a project directory for all your projects and then a subdirectory for each project.
Follow along now if you have Rust installed, or try at your first opportunity later.
$ mkdir ~/projects
$ cd ~/projects
$ mkdir hello_world
$ cd hello_world
All Rust source files have the extension .rs.
Create and edit a file called main.rs.
For example with the nano editor on MacOS
# From MacoS terminal
nano main.rs
or notepad on Windows
# From Windows CMD or PowerShell
notepad main.rs
and add the following code:
fn main() { println!("Hello, world!"); }
Note: Since our course notes are in
mdbook, code cells like above can be executed right from the notes!In many cases we make the code cell editable right on the web page!
If you created that file on the command line, then you compile and run the program with the following commands:
$ rustc main.rs # compile with rustc which creates an executable
If it compiled correctly, you should have a new file in your directory
For example on MacOS or Linux you might see:
hello_world % ls -l
total 880
-rwxr-xr-x 1 tgardos staff 446280 Sep 10 21:03 main
-rw-r--r-- 1 tgardos staff 45 Sep 10 21:02 main.rs
Question: What is the new file? What do you observe about the file properties?
On Windows you'll see main.exe.
$ ./main # run the executable
Hello, world!
Compiled (e.g. Rust) vs. Interpreted (e.g. Python)
Python: One Step (Interpreted)
python hello.py
- Python reads your code line by line and executes it immediately
- No separate compilation step needed
Rust: Two Steps (Compiled)
# Step 1: Compile (translate to machine code)
rustc hello.rs
# Step 2: Run the executable
./hello
rustcis your compilerrustctranslates your entire program to machine code- Then you run the executable (why
./?)
The main() function
fn main() { ... }
is how you define a function in Rust.
The function name main is reserved and is the entry point of the program.
The println!() Macro
Let's look at the single line of code in the main function:
println!("Hello, world!");Rust convention is to indent with 4 spaces -- never use tabs!!
println!is a macro which is indicated by the!suffix.- Macros are functions that are expanded at compile time.
- The string
"Hello, world!"is passed as an argument to the macro.
The line ends with a ; which is the end of the statement.
More Printing Tricks
Let's look at a program that prints in a bunch of different ways.
// A bunch of the output routines fn main() { let x = 9; let y = 16; print!("Hello, DS210!\n"); // Need to include the newline character println!("Hello, DS210!\n"); // The newline character here is redundant println!("{} plus {} is {}", x, y, x+y); // print with formatting placeholders //println!("{x} plus {y} is {x+y}"); // error: cannot use `x+y` in a format string println!("{x} plus {y} is {}\n", x+y); // but you can put variable names in the format string }
More on println!
- first parameter is a format string
{}are replaced by the following parameters
print! is similar to println! but does not add a newline at the end.
To dig deeper on formatting strings:
fmtmodule- Format strings syntax
Input Routines
Here's a fancier program. You don't have to worry about the details, but
paste it into a file name.rs, run rustc name.rs and then ./name.
// And some input routines
// So this is for demo purposes
use std::io;
use std::io::Write;
fn main() {
let mut user_input = String::new();
print!("What's your name? ");
io::stdout().flush().expect("Error flushing"); // flush the output and print error if it fails
let _ =io::stdin().read_line(&mut user_input); // read the input and store it in user_input
println!("Hello, {}!", user_input.trim());
}Project manager: cargo
Rust comes with a very helpful project and package manager: cargo
-
create a project:
cargo new PROJECT-NAME -
main file will be
PROJECT-NAME/src/main.rs -
to run:
cargo run -
to just build:
cargo build
Cargo example
~ % cd ~/projects
projects % cargo new cargo-hello
Creating binary (application) `cargo-hello` package
note: see more `Cargo.toml` keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html
projects % cd cargo-hello
cargo-hello % tree
.
├── Cargo.toml
└── src
└── main.rs
2 directories, 2 files
cargo-hello % cargo run
Compiling cargo-hello v0.1.0 (/Users/tgardos/projects/cargo-hello)
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.21s
Running `target/debug/cargo-hello`
Hello, world!
% tree -L 3
.
├── Cargo.lock
├── Cargo.toml
├── src
│ └── main.rs
└── target
├── CACHEDIR.TAG
└── debug
├── build
├── cargo-hello
├── cargo-hello.d
├── deps
├── examples
└── incremental
8 directories, 6 files
Cargo --release
By default, cargo makes a slower debug build that has extra
debugging information.
We'll see more about that later.
Add --release to create a "fully optimized" version:
- longer compilation
- faster execution
- some runtime checks not included (e.g., integer overflow)
- debuging information not included
- the executable in a different folder
cargo-hello (master) % cargo build --release
Compiling cargo-hello v0.1.0 (/Users/tgardos/projects/cargo-hello)
Finished `release` profile [optimized] target(s) in 0.38s
(.venv) √ cargo-hello (master) % tree -L 2
.
├── Cargo.lock
├── Cargo.toml
├── src
│ └── main.rs
└── target
├── CACHEDIR.TAG
├── debug
└── release
5 directories, 4 files
Cargo check
If you just want to check if your current version compiles: cargo check
- Much faster for big projects
Hello Rust Activity
-
Get in groups of 3+
-
Place the lines of code in order in two parts on the page: your shell, and your code file
main.rsto make a reasonable sequence and functional code. -
We'll take the last 5 minutes to share solutions
-
Don't stress if you didn't finish! Just paste what you have into GradeScope.
println!("Good work! Average: {:.1}", average);
cargo run
scores.push(88);
git push -u origin main
let average = total as f64 / scores.len() as f64;
cargo new hello_world
} else if average >= 80.0 {
nano src/main.rs
let total: i32 = scores.iter().sum();
if average >= 90.0 {
touch README.md
cd hello_world
fn main() {
git add src/main.rs
println!("Keep trying! Average: {:.1}", average);
let mut scores = vec![85, 92, 78, 96];
ls -la
echo "This is a grade average calculator" > README.md
} else {
git commit -m "Add calculator functionality"
}}
println!("Excellent! Average: {:.1}", average);
Overview of Programming languages
Learning Objectives
- Programming languages
- Describe the differences between a high level and low level programming language
- Describe the differences between an interpreted and compiled language
- Describe the differences between a static and dynamically typed language
- Know that there are different programming paradigms such as imperative and functional
- Describe the different memory management techniques
- Be able to identify the the properties of a particular language such as rust.
Various Language Levels
-
Native code
- usually compiled output of a high-level language, directly executable on target processor
-
Assembler
- low-level but human readable language that targets processor
- pros: as fine control as in native code
- cons: not portable
-
High level languages
- various levels of closeness to the architecture: from C to Prolog
- efficiency:
- varies
- could optimize better
- pros:
- very portable
- easier to build large projects
- cons:
- some languages are resource–inefficient
Assembly Language Examples
ARM X86
. text section .text
.global _start global _start
_start: section .data
mov r0, #1 msg db 'Hello, world!',0xa
ldr r1, =message len equ 0xe
ldr r2, =len section .text
mov r7, #4 _start:
swi 0 mov edx,len ;message length
mov r7, #1 mov ecx,msg ;message to write
mov ebx,1 ;file descriptor (stdout)
.data. mov eax,4 ;system call number (sys_write)
message: int 0x80 ;call kernel
.asciz "hello world!\n" mov ebx,0 ;process' exit code
len = .-message. mov eax,1 ;system call number (sys_exit)
int 0x80 ;call kernel - this interrupt won't return
Interpreted vs. compiled
Interpreted:
- An application (interpreter) reads commands one by one and executes them.
- One step process to run an application:
python hello.py
("Fully") Compiled:
- Translated to native code by compiler
- Usually more efficient
- Two steps to execute:
- Compile (Rust:
rustc hello.rs) - Run (Rust:
./hello)
- Compile (Rust:
Compiled to Intermediate Representation (IR):
- Example: Java
- Portable intermediate format
- Needs another application, Java virtual machine, that knows how to interpret it
- Example: Python
- Under some circumstances Python bytecode is created and cached in
__pycache__ - Python bytecode is platform independent and executed by the Python Virtual Machine
- Under some circumstances Python bytecode is created and cached in
Just-in-Time (JIT) compilation is an interesting wrinkle in that it can take interpreted and intermediate format languages and compile them down to machine code.
Type checking: static vs. dynamic
Dynamic (e.g., Python):
- checks if an object can be used for specific operation during runtime
- pros:
- don't have to specify the type of object
- procedures can work for various types
- faster or no compilation
- cons:
- slower at runtime
- problems are detected late
Consider the following python code.
def add(x,y):
return x + y
print(add(2,2))
print(add("a","b"))
print(add(2,"b"))
4
ab
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[1], line 6
4 print(add(2,2))
5 print(add("a","b"))
----> 6 print(add(2,"b"))
Cell In[1], line 2, in add(x, y)
1 def add(x,y):
----> 2 return x + y
TypeError: unsupported operand type(s) for +: 'int' and 'str'
There is optional typing specification, but it is not enforced, e.g. accepting ints.
import typing
def add(x:str, y:str) -> str:
return x + y
print(add(2,2)) # doesn't complain about getting integer types
print(add("ab", "cd"))
#print(add(2,"n"))
4
abcd
- You can use packages such as
pyrightormypyas a type checker before running your programs - Supported by VSCode python extension
Type checking: static vs. dynamic
Static (e.g, C++, Rust, OCaml, Java):
- checks if types of objects are as specified
- pros:
- faster at runtime
- type mismatch detected early
- cons:
- often need to be explicit with the type
- making procedures generic may be difficult
- potentially slower compilation
C++:
int add(int x, int y) {
return x + y;
}
Rust:
#![allow(unused)] fn main() { fn add(x:i32, y:i32) -> i32 { x + y } }
Type checking: static vs. dynamic
Note: some languages are smart and you don't have to always specify types (e.g., OCaml, Rust)
Rust:
#![allow(unused)] fn main() { let x : i32 = 7; let y = 3; // Implied to be default integer type let z = x * y; // Type of result derived from types of operands }
Various programming paradigms
- Imperative
- Functional
- Object-oriented
- Declarative / programming in logic
Imperative
im·per·a·tive (adjective) -- give an authoritive command
# Python -- Imperative
def factorial(N):
ret = 1
for i in range(N):
ret = ret * i
return ret
Functional
; Scheme, a dialect of lisp -- functional
(define (factorial n) (cond ((= n 0) 1)
(t (* n (factorial (- n 1))))))
Object Oriented
// C++ -- Object oriented pattern
class Factorial {
private:
int64 value;
public:
int64 factorial(int input) {
int64 temp = 1;
for(int i=1; i<=input; i++) {
temp = temp * i;
}
value = temp
}
int64 get_factorial() {
return value;
}
}
Declarative/Logic
% Prolog -- declaritive / programming in logic
factorial(0,1). % Base case
factorial(N,M) :-
N>0, % Ensure N is greater than 0
N1 is N-1, % Decrement N
factorial(N1, M1), % Recursive call
M is N * M1. % Calculate factorial
Memory management: manual vs. garbage collection
At least 3 kinds:
- Manual (e.g. C, C++)
- Garbage collection (e.g. Java, Python)
- Ownership-based (e.g. Rust)
Manual
- Need to explicitly ask for memory and return it
- pros:
- more efficient
- better in real–time applications
- cons:
- more work for the programmer
- more prone to errors
- major vector for attacks/hacking
Example below in C++.
Garbage collection
- Memory freed automatically
- pros:
- less work for the programmer
- more difficult to make mistakes
- cons:
- less efficient
- can lead to sudden slowdowns
Ownership-Based
- Keeps track of memory object ownership
- Allows borrowing, references without borrowing, move ownership
- When object goes out of scope, Rust automatically deallocates
- Managed deterministically at compile-time, not run-time like garbage collection
We'll dive deeper into Rust ownership later.
Rust Language (Recap)
-
high–level
-
imperative
-
compiled
-
static type checking
-
ownership-based memory management
Most important difference between Python and Rust?
How do we denote blocks of code?
- Python: indentation
- Rust:
{...}
| Language | formatting | scoping |
|---|---|---|
| Python | indentation | indentation |
| Rust | indentation | braces, {} |
Example in Rust
#![allow(unused)] fn main() { fn hi() { println!("Hello!"); println!("How are you?"); } }
Don't be afraid of braces!!! You'll encounter them in C, C++, Java, Javascript, PHP, Rust, ...
Memory Structure of an Executable Program
It's very helpful to have conceptual understanding of how memory is structured in executable programs.
The figure below illustrates a typical structure, where some low starting memory address is at the bottom and then memory addresses increase as you go up in the figure.
Here's a short description of each section starting from the bottom:
- text -- the code, e.g. program instructions
- initialized data -- explicitly initialized global/static variables
- uninitialized data (bss) -- uninitialized global/static variables, generally auto-initialied to zero. BSS -- Block Started by Symbol
- heap -- dynamically allocated memory. grows as structures are allocated
- stack -- used for local variables and function calls
Example of unsafe programming in C
Let's take a look at the problem with the following C program which asks you to guess a string and hints whether your guess was lexically less or greater.
- Copy the code into a file
unsafe.c - Compile with a local C compiler, for example,
cc unsafe.c - Execute program, e.g.
./a.out
Try with the following length guesses:
- guesses of string length <= 20
- guesses of string length > 20
- guesses of string length >> 20
Pay attention to the printout of
secretString!
Lecture Note: Switch to code
#include <signal.h>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int main(){
char loop_bool[20];
char secretString[20];
char givenString[20];
char x;
int i, ret;
memset(&loop_bool, 0, 20);
for (i=0;i<19;i++) {
x = 'a' + random() % 26;
secretString[i] = x;
}
printf("secretString: %s\n", secretString);
while (!loop_bool[0]) {
gets(givenString);
ret = strncmp(secretString, givenString, 20);
if (0 == ret) {
printf("SUCCESS!\n");
break;
}else if (ret < 0){
printf("LESS!\n");
} else {
printf("MORE!\n");
}
printf("secretString: %s\n", secretString);
}
printf("secretString: %s\n", secretString);
printf("givenString: %s\n", givenString);
return 0;
}
A Brief Aside -- The people behind the languages
Who are these people?
- Guido Van Rossum
- Graydon Hoare
- Bjarne Stroustrup
- James Gosling
- Brendan Eich
- Brian Kernighan and Dennis Ritchie
Who are these people?
- Guido Van Rossum -- Python
- Graydon Hoare -- Rust
- Bjarne Stroustrup -- C++
- James Gosling -- Java
- Brendan Eich -- Javascript
- Brian Kernighan and Dennis Ritchie -- C
Recap
Guessing Game Part 1
Building a very small Rust application.
Guessing Game Part 1
We're going to build on "Hello Rust" to write a small guessing game program.
You're not expected to understand all the details of all the code, but rather start getting familiar with the language and with building applications.
Let's eat the cake 🍰 and then we'll learn the recipe👨🍳.
Tip: Follow along in your terminal or PowerShell window.
Learning objectives:
By the end of this module you should be able to:
- Use basic
cargocommands to create projects and compile rust code - Add external dependencies (crates) to a project
- Recognize some useful syntax like Rust's
Resulttype with.expect() - Recognize and fix some common Rust compilation errors
Keep Practicing with the Terminal
- This is Part 1 where we use the terminal
- In Part 2, we will start using VSCode which integrates
- code editor
- terminal window
- compiler hints
- AI assistance
Guessing game demo
Compiling review and reference
Option 1: Compile directly
- put the content in file
hello.rs - command line:
- navigate to this folder
rustc hello.rs- run
./helloorhello.exe
Option 2: Use Cargo
- create a project:
cargo new PROJECT-NAME - main file will be
PROJECT-NAME/src/main.rs - to build and run:
cargo run - the machine code will be in :
./target/debug/PROJECT-NAME
Different ways to run Cargo
cargo runcompiles, runs, and saves the binary/executable in/target/debugcargo buildcompiles but does not runcargo checkchecks if it compiles (fastest)cargo run --releasecreates (slowly) "fully optimized" binary in/target/release
Back to the guessing game
In MacOS terminal or Windows PowerShell, go to the folder you created to hold all your projects:
cd ~/projects
Let's use cargo to create a project:
cargo new guessing-game
Replace the contents of src/main.rs with:
use std::io;
fn main() {
println!("Guess the number!");
println!("Please input your guess.");
let mut guess = String::new();
// This is all technically one line of code
io::stdin()
.read_line(&mut guess)
.expect("Failed to read line");
println!("You guessed: {}", guess);
}And then:
cargo run
Question: Program doesn't do much? How can we improve it?
More on variables
Let's take a look at this variable assignment:
#![allow(unused)] fn main() { let mut guess = String::new(); }
As we saw in the earlier module, we assign a variable with let as in
#![allow(unused)] fn main() { let count = 5; }
But by default Rust variables are immutable.
Definition:
im·mu·ta·ble
adjective
unchanging over time or unable to be changed
"an immutable fact"
Try executing the following code cell.
fn main() { let count = 5; count = 7; }
Rust compiler errors are pretty descriptive!
error[E0384]: cannot assign twice to immutable variable `count`
--> src/main.rs:4:1
|
3 | let count = 5;
| ----- first assignment to `count`
4 | count = 7;
| ^^^^^^^^^ cannot assign twice to immutable variable
|
help: consider making this binding mutable
|
3 | let mut count = 5;
| +++
For more information about this error, try `rustc --explain E0384`.
error: could not compile `playground` (bin "playground") due to 1 previous error
It often even tells you how to correct the error with the mut keyword to make
the variable mutable.
#![allow(unused)] fn main() { let mut count = 5; count = 7; }
Question: Why might it be helpful to have variables be immutable by default?
.expect() - a tricky concept
We'll go into all of this more later, but:
read_line()returns aResulttype which has two variants -OkandErrOkmeans the operation succeeded, and returns the successful valueErrmeans something went wrong, and it returns the string you passed to.expect()
More in a few future module.
More on macros!
- A macro is code that writes other code for you / expands BEFORE it compiles.
- They end with ! like println!, vec!, or panic!
For example, println!("Hello"); roughly expands into
#![allow(unused)] fn main() { use std::io::{self, Write}; io::stdout().write_all(b"Hello\n").unwrap(); }
while println!("Name: {}, Age: {}", name, age); expands into
#![allow(unused)] fn main() { use std::io::{self, Write}; io::stdout().write_fmt(format_args!("Name: {}, Age: {}\n", name, age)).unwrap(); }
Rust Crates
In Rust, the collection files in a project form a "crate".
You can have:
- binary or application crate, that you can execute directly, or a
- library crate, which you can use in your application
Rust makes it super easy to publish and use crates.
See crates.io.
Using crates: generate a random number
We want to add a random number, so we need a way of generating them.
Rust doesn't have a random number generator in its standard library
so we will use a crate called rand.
We can do that with the command:
cargo add rand
which will produce an output like...
Output
% cargo add rand
Updating crates.io index
Adding rand v0.9.2 to dependencies
Features:
+ alloc
+ os_rng
+ small_rng
+ std
+ std_rng
+ thread_rng
- log
- nightly
- serde
- simd_support
- unbiased
Updating crates.io index
Locking 17 packages to latest Rust 1.85.1 compatible versions
Adding cfg-if v1.0.3
Adding getrandom v0.3.3
Adding libc v0.2.175
Adding ppv-lite86 v0.2.21
Adding proc-macro2 v1.0.101
Adding quote v1.0.40
Adding r-efi v5.3.0
Adding rand v0.9.2
Adding rand_chacha v0.9.0
Adding rand_core v0.9.3
Adding syn v2.0.106
Adding unicode-ident v1.0.19
Adding wasi v0.14.5+wasi-0.2.4
Adding wasip2 v1.0.0+wasi-0.2.4
Adding wit-bindgen v0.45.1
Adding zerocopy v0.8.27
Adding zerocopy-derive v0.8.27
Take a look at Cargo.toml now.
cat Cargo.toml
[package]
name = "guessing-game-part1"
version = "0.1.0"
edition = "2024"
[dependencies]
rand = "=0.8.5"
Note that the version number is captured.
Also take a look at Cargo.lock.
It's kind of like pip freeze or conda env export in that it
fully specifies your environment down to the package versions.
Generate Random Number
So now that we've specified that we will use the rand
crate, we add to our main.rs:
#![allow(unused)] fn main() { use rand::Rng; }
after the use std::io, and add right after fn main() {
#![allow(unused)] fn main() { let secret_number = rand::rng().random_range(1..=100); println!("The secret number is: {secret_number}"); }
Run your program. Whaddayathink so far?
Let's Check Guess
Obviously, we better compare the guess to the "secret number".
Add the following code to the end of your main function.
#![allow(unused)] fn main() { if guess == secret_number { println!("You win!"); } else { println!("You lose!"); } }
And run your program again. 🤔
In-Class Activity: Compiler Error Hints!
This activity is designed to teaching you to to not fear compiler errors and to show you that Rust's error messages are actually quite helpful once you learn to read them!
Please do NOT use VSCode yet! Open your files in nano, TextEdit / Notepad or another plain text editor.
Instructions
The code asks the user for a series of integers, one at a time, then counts the number, sum and average.
But there are four syntax errors in the code.
Working in pairs, fix the syntax errors based on the compiler error messages.
Put a comment (using double backslashes, e.g. \\ comment) either on the line
before or at the end of the stating what you changed to fix the error.
Paste the corrected code into Gradescope.
I'll give you a 2 minute warning to wrap up in gradescope and then we'll review the errors.
Again Please do NOT use VSCode yet! It ruins the fun
Setup Instructions
Go to your projects folder and create a new Rust project.
cd ~/projects # or whatever your main projects folder is called
cargo new compiler-errors
cd compiler-errors
cargo add rand
# quick test of the default project
cargo run
You should see "Hello World!" without any errors.
Starter Code (src/main.rs)
Replace the code in main.rs with the following code.
use std::io::{self, Write}; fn main() { println!("Enter integers, one per line. Empty line to finish.") let nums: Vec<i32> = Vec::new() loop { print!("> "); io::stdout().flush().unwrap(); let mut input = String::new(); if io::stdin().read_line(&mut input).is_err() { return; } let trimmed = input.trim(); if trimmed.is_empty(): break; match trimmed.parse::<i32>() { Ok(n) => nums.push(n), Err(_) => println!("Please enter a valid integer."), } } if nums.is_empty() { println!("No numbers entered."); } else { let sum: i32 = nums.iter().sum(); let avg = sum as f64 / nums.len() as f64; println!("Count = {nums.len()}, Sum = {sum}, Average = {avg:.2}"); } }
- Compile the code
- Read the compiler output, starting from the top
- Fix the error
- Repeat...
List of Errors
What did you find?
- error 1:
- error 2:
- error 3:
- error 4:
Recap
- Variables in Rust are immutable by default - we need to explicitly mark them as
mutto make them mutable - The
letkeyword is used for variable declaration and initialization in Rust - Rust has strong error handling with
Resulttypes that haveOkandErrvariants - The
.expect()method is used to handle potential errors by unwrapping theResultor panicking with a message - Basic I/O in Rust uses the
std::iomodule for reading from stdin and writing to stdout
Topics
- Numbering Systems
- The Von Neumann Architecture
- Memory Hierarchy and Memory Concepts
- Trends, Sizes and Costs
Numbering Systems
- Decimal (0-9) e.g. 1724
- Binary (0-1) e.g. 0b011000 (24 decimal)
- Octal (0-7) e.g. 0o131 (89 decimal)
- Hexadecimal (0-9, A-F) e.g 0x13F (319 decimal)
Converting between numbering systems
For any base b to decimal. Assume number C with digits
Between octal and binary
Every octal digit corresponds to exactly 3 binary digits and the reverse. For example 0o34 = 0b011_100. Traverse numbers right to left and prepend with 0s if necessary.
Between hexadecimal and binary
Every hexadecimal digit corresponds to exactly 4 binary digits and the reverse. For example 0x3A = 0b0011_1010. Traverse numbers right to left and prepend with 0s if necessary.
Between decimal and binary (or any base b)
More complicated. Divide repeatedly by 2 (or the base b) and keep the remainder as the next most significant binary digit. Stop when the division returns 0.
i = 0
while D > 0:
C[i] = D % 2 # modulo operator -- or substitute 2 for any base b
D = D // 2 # floor division -- or substitute 2 for any base b
i += 1
What about between decimal and octal/hexadecimal
You can use the same logic as for binary or convert to binary and then use the binary to octal/hexadecimal simple conversions
The Von Neuman Architecture
Named after the First Draft of a Report on the EDVAC written by mathematician John von Neuman in 1945.
Most processor architectures are still based on this same model.

Key Components
- Central Processing Unit (CPU):
- The CPU is the core processing unit responsible for executing instructions and performing computations. It consists of:
- Control Unit (CU):
- Directs the operations of the CPU by interpreting instructions and coordinating data flow between the components.
- Controls the flow of data between the input, memory, and output devices.
- Arithmetic/Logic Unit (ALU):
- Performs arithmetic operations (e.g., addition, subtraction) and logical operations (e.g., AND, OR, NOT).
- Acts as the computational engine of the CPU.
- Memory Unit:
- Stores data and instructions needed for processing.
- The memory serves as temporary storage for instructions being executed and intermediate data.
- It communicates with both the CPU and input/output devices.
- Input Device:
- Provides data or instructions to the CPU.
- Examples include keyboards, mice, and sensors.
- Data flows from the input device into the CPU for processing.
- Output Device:
- Displays or transmits the results of computations performed by the CPU.
- Examples include monitors, printers, and actuators.
Also known as the stored program architecture
Both data and program stored in memory and it's just convention which parts of memory contain instructions and which ones contain variables.
Two very special registers in the processor: Program Counter (PC) and Stack Pointer (SP)
PC: Points to the next instruction. Auto-increments by one when instruction is executed with the exception of branch and jmp instructions that explicitly modify it. Branch instructions used in loops and conditional statements. Jmp instructions used in function calls.
SP: Points to beginning of state (parameters, local variables, return address, old stackpointer etc) for current function call.
Intruction Decoding
Use the Program Counter to fetch the next instruction. After fetching you have to decode it, and subsequently to execute it.
Decoding instructions requires that you split the instruction number to the opcode (telling you what to do) and the operands (telling what data to operate one)
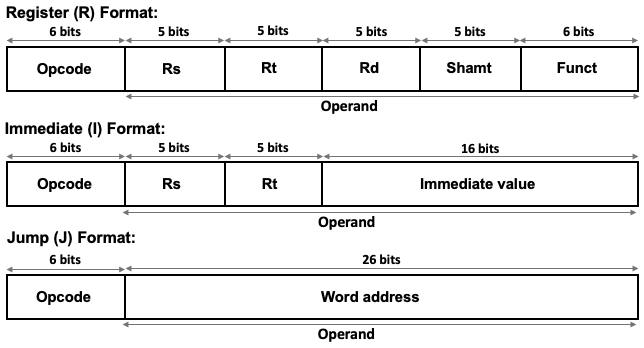
Example from MIPS (Microprocessor without Interlocked Pipeline Stages) Intruction Set Architecture (ISA). MIPS is RISC (Reduced Instruction Set Computer).
The time cost of operations
Assume for example a processor clocked at 2 GHz, e.g. .
- Executing an instruction ~ 0.5 ns (1 clock cycle)
- Getting a value (4 bytes) from L1 cache ~1 ns
- Branch mispredict ~3 ns
- Getting a value from L2 cache ~4 ns
- Send 1Kbyte of data over 1Gbps network (just send not arrive) ~ 16 ns
- Get a value from main memory ~100 ns
- Read 1MB from main memory sequentially ~1000 ns
- Compress 1Kbyte (in L1 cache) with zippy ~2000 ns
- Read 1MB from SSD ~49,000 µs
- Send a ping pong packet inside a datacenter ~500,000 ns
- Read 1Mbyte from HDD ~825,000 ns
- Do an HDD seek ~2,000,000 ns
- Send a packet from US to Europe and back ~150,000,000 ns
https://samwho.dev/numbers/
The memory hierarchy and memory concepts
We've talked about different kinds of memory. It's helpful to think of it in terms of a hierarchy.
- As indicated above, registers are closest to the processor and fastest.
- As you move farther away, the size gets larger but access gets slower
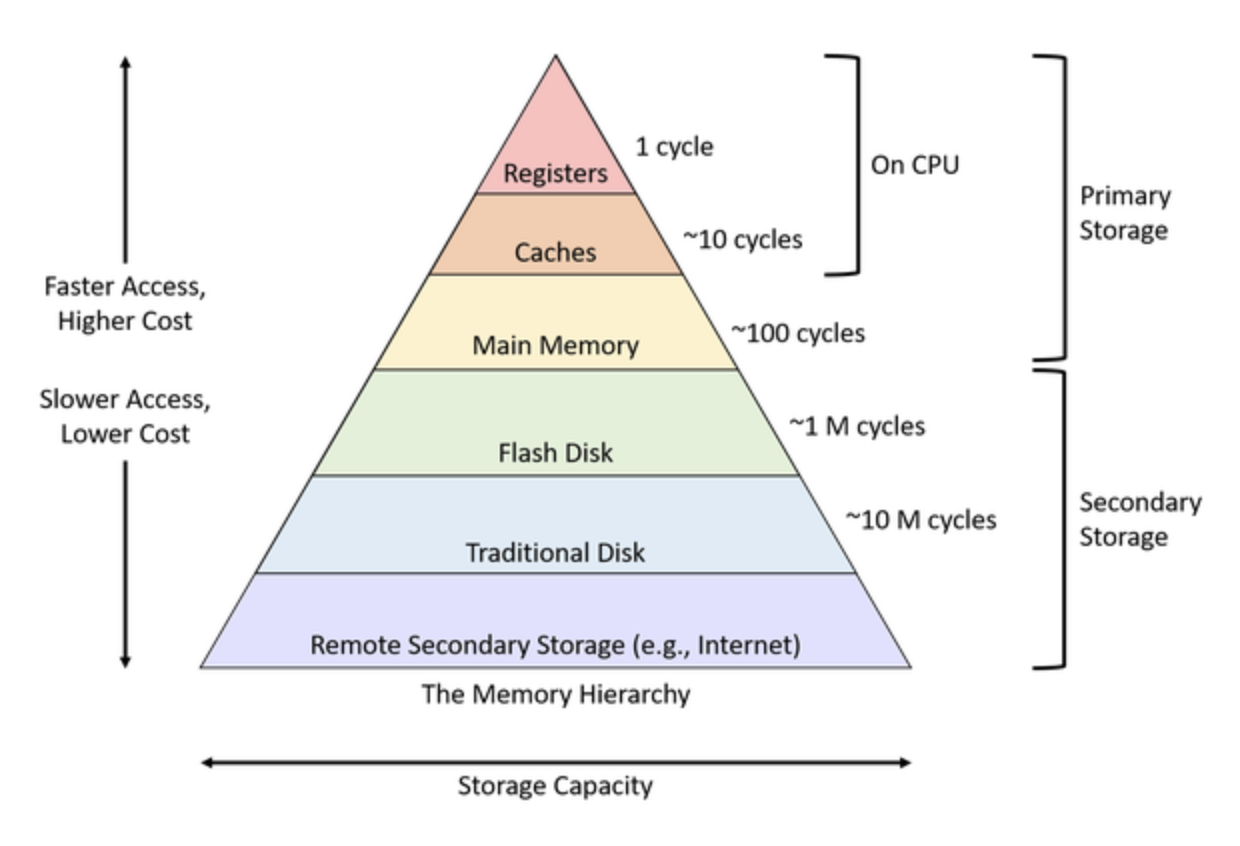
The following figure from Hennesy and Patterson is also very informative.
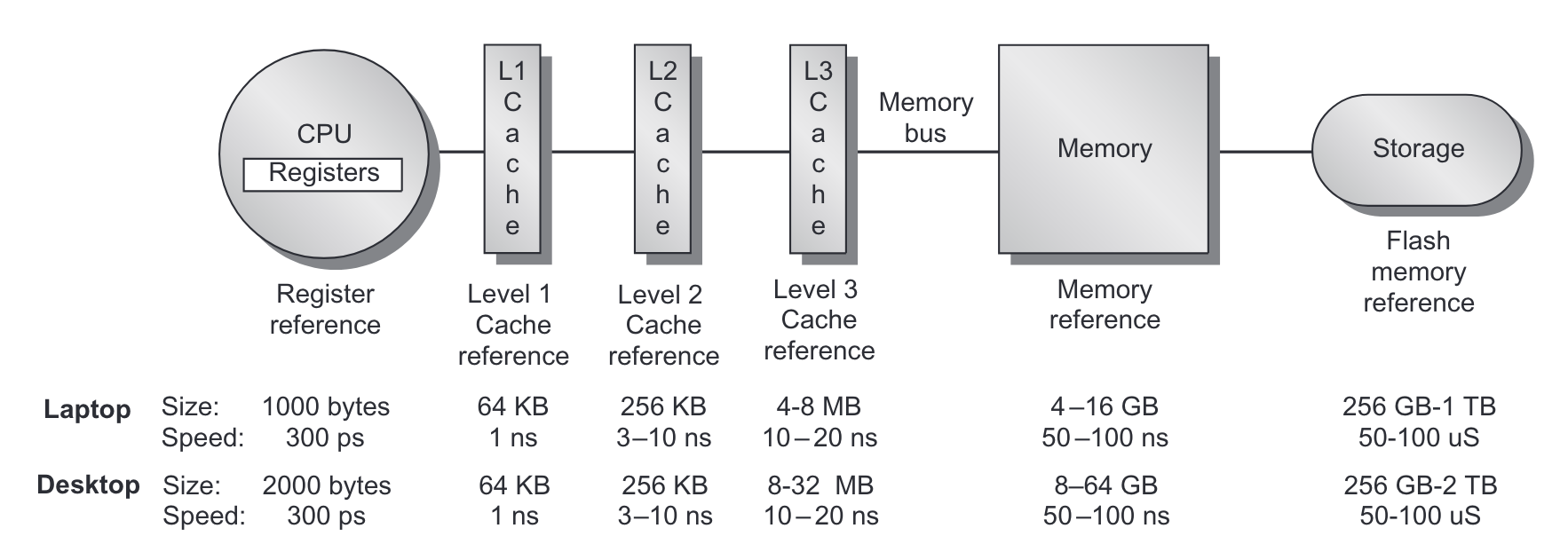 From Hennesy and Patterson, Computer Architecture: A Quantitative Approach_.
From Hennesy and Patterson, Computer Architecture: A Quantitative Approach_.
When the CPU tries to read from a memory location it
- First checks if that memory location is copied to L1 cache
- if it is, then the value is returned
- if it is not...
- Then checks if the memory location is copied to L2 cache
- if it is, then the value is copied to L1 cache and returned
- if it is not...
- Then checks if the memory location is copied to L3 cache
- if it is, then the value is copied to L2, then L1 and returned
- if it is not...
- Go to main memory
- fetch a cache line size of data, typically 64 bytes (why?)
More on Caches
- Each cache line size of memory can be mapped to one of cache slots in each cache
- we say such a cache is -way
- if all slots are occupied, then we evict the Least Recently Used (LRU) slots
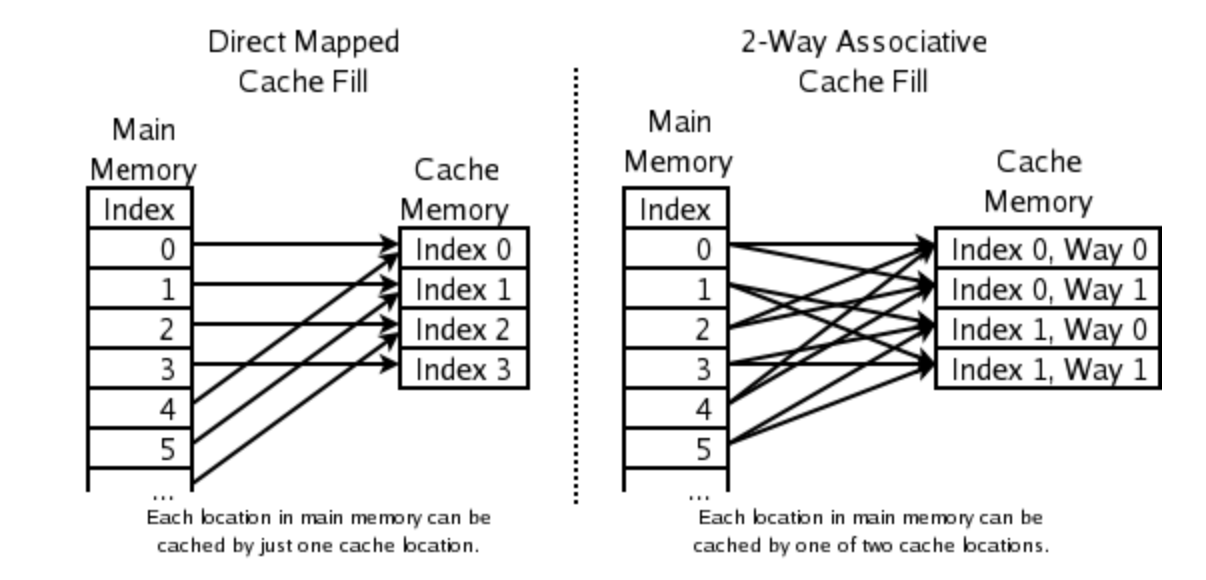
Direct mapped versus 2-way cache mapping. Wikipedia: CPU cache
We can see the cache configuration on a Linux system with the getconf command.
Here's the output from the MOC.
$ getconf -a | grep CACHE
LEVEL1_ICACHE_SIZE 32768 (32KB)
LEVEL1_ICACHE_ASSOC 8
LEVEL1_ICACHE_LINESIZE 64
LEVEL1_DCACHE_SIZE 32768 (32KB)
LEVEL1_DCACHE_ASSOC 8
LEVEL1_DCACHE_LINESIZE 64
LEVEL2_CACHE_SIZE 1048576 (1MB)
LEVEL2_CACHE_ASSOC 16
LEVEL2_CACHE_LINESIZE 64
LEVEL3_CACHE_SIZE 23068672 (22MB)
LEVEL3_CACHE_ASSOC 11
LEVEL3_CACHE_LINESIZE 64
LEVEL4_CACHE_SIZE 0
LEVEL4_CACHE_ASSOC 0
LEVEL4_CACHE_LINESIZE 0
How many way associative are they?
Why is 32kb not 32,000? When is K 1,000?
An 8-way associative cache with 32 KB of size and 64-byte blocks divides the cache into 64 sets, each with 8 cache lines. Memory addresses are mapped to specific sets.
Benefits of 8-Way Associativity:
- Reduces Conflict Misses:
- Associativity allows multiple blocks to map to the same set, reducing the likelihood of eviction due to conflicts.
- Balances Complexity and Performance:
- Higher associativity generally improves hit rates but increases lookup complexity. An 8-way cache strikes a good balance for most applications.
Cache Use Examples
Example from this blog post.
Contiguous read loop

// cache1.cpp
#include <time.h>
#include <stdio.h>
#include <stdlib.h>
/*
* Contiguous access loop
*
* Example from https://mecha-mind.medium.com/demystifying-cpu-caches-with-examples-810534628d71
*
* compile with `clang cache.cpp -o cache`
* run with `./cache`
*/
int main(int argc, char* argv[]) {
const int length = 512 * 1024 * 1024; // 512M
const int cache_line_size = 16; // size in terms of ints (4 bytes) so 16 * 4 = 64 bytes
const int m = length/cache_line_size; // 512M / 32 = 32M
printf("Looping %d M times\n", m/(1024*1024));
int *arr = (int*)malloc(length * sizeof(int)); // 512M length array
clock_t start = clock();
for (int i = 0; i < m; i++) // loop 32M times with contiguous access
arr[i]++;
clock_t stop = clock();
double duration = ((double)(stop - start)) / CLOCKS_PER_SEC * 1000;
printf("Duration: %f ms\n", duration);
free(arr);
return 0;
}
When running on Apple M2 Pro.
% clang cache1.cpp -o cache1
% ./cache1
Looping 32 M times
Duration: 54.166000 ms
Now let's modify the loop to jump by intervals of cache_line_size
Noncontiguous Read Loop

// cache2.cpp
for (int i = 0; i < m*cache_line_size; i+=cache_line_size) // non-contiguous access
arr[i]++;
clock_t stop = clock();
% ./cache2
Looping 32 M times
Duration: 266.715000 ms
About 5X slower. What happened?
Noncontiguous with 2x cache line jump
We loop half the amount of times!!
for (int i = 0; i < m*cache_line_size; i+=2*cache_line_size) {
arr[i]++;
arr[i+cache_line_size]++;
}
When running on Apple M2 Pro.
% ./cache3
Looping 16 M times
Duration: 255.551000 ms
Caches on multi-processor systems
For multi-processor systems (which are now standard), memory hierarchy looks something like this:
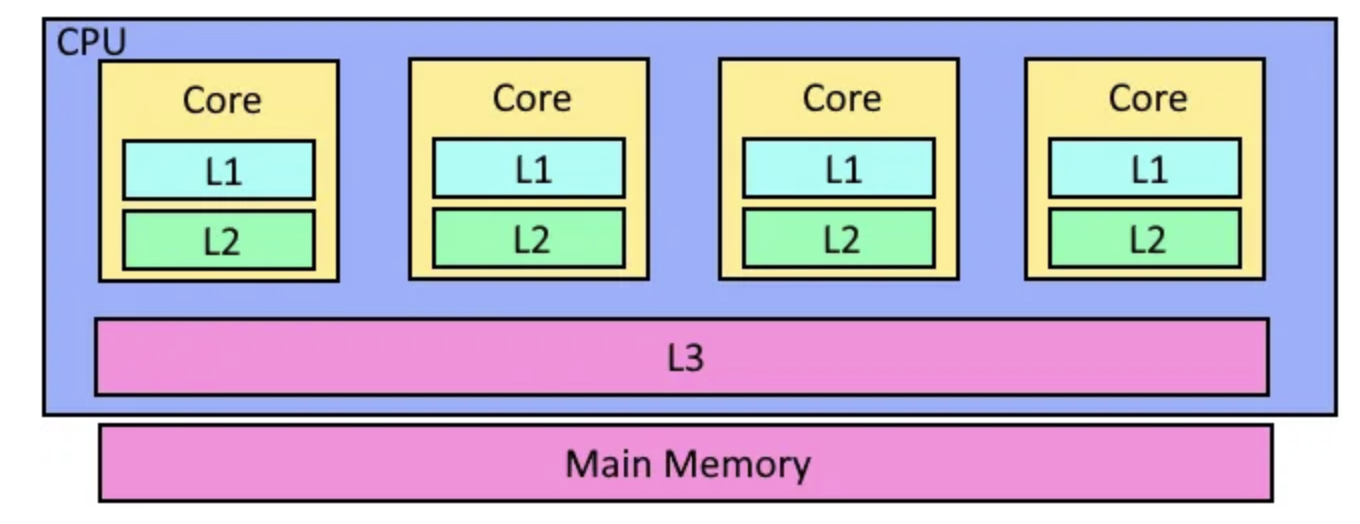
In other words, each core has it's own L1 and L2 cache, but the L3 cache and of course main memory is shared.
Virtual Memory, Page Tables and TLBs
- The addressable memory address range is much larger than available physical memory
- Every program thinks it can access every possible memory address.
- And there has to exist some security to prevent one program from modifying the memory occupied by another.
- The mechanism for that is virtual memory, paging and address translation

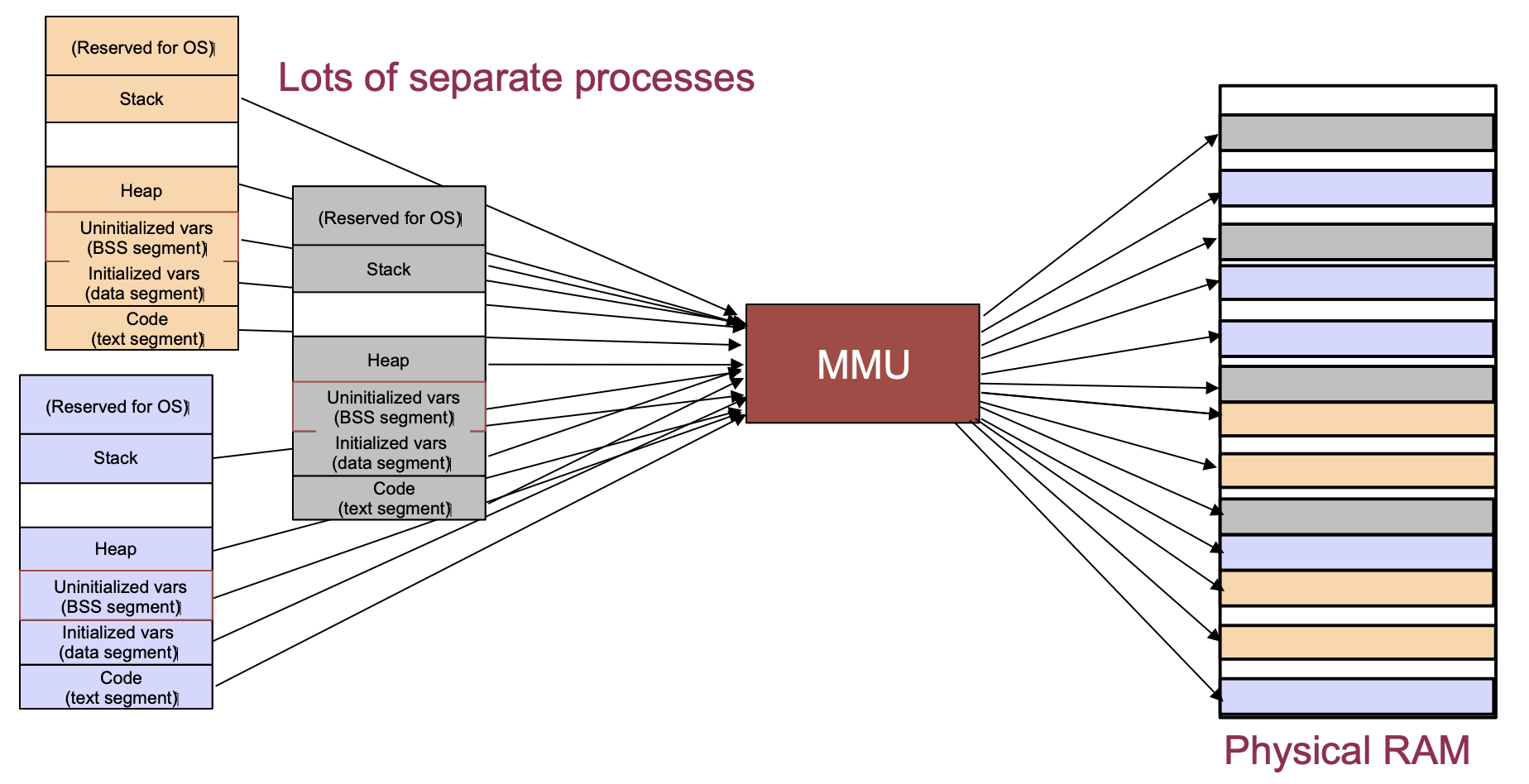 From University of Illinois CS 241 lecture notes.
From University of Illinois CS 241 lecture notes.
Page sizes are typically 4KB, 2MB or 1GB depending on the operating system.
If you access a memory address that is not paged into memory, there is a page fault while a page is possible evicted and a the memory is loaded from storage into memory.
Trends, Sizes and Costs
We'll finish by looking at some representative costs, sizes and computing "laws."
Costs
- Server GPU: \500-$1000
- DRAM: \0.05-$.01/Gbyte
- Disk: \0.02-$0.14/Gbyte
Sizes
For a typical server
2 X 2Ghz Intel/ADM processors
32-128Gbytes of memory
10-100 Tbytes of storage
10Gbps Network card
1-2 KWatts of power
For a typical datacenter
100K - 1M sercers
1+ MWatt of power
1-10 Pbbs of internal bandwidth, 1-10 Tbps of Internet facing bandwidth
1-10 Exabytes of storage
Trends
Computers grow fast so we have written some rules of thumb about them
- Kryder's Law -- Storage density doubles every 12 months
- Nielsen's Law -- Consumer Bandwidth doubles every 20 months
- Moore's Law -- CPU capacity doubles every 18 months
- Metcalfe's Law -- The value of a Network increases with the square of its members
- Bell's Law -- Every 10 years the computing paradigm changes
In Class Poll
Guessing Game Part 2: VSCode & Completing the Game
Learning objectives
By the end of class today you should be able to:
- Use VSCode with rust-analyzer and the integrated terminal for Rust development
- Start using loops and conditional logic in Rust
- Use
matchexpressions andOrderingfor comparisons - Keep your code tidy and readable with
clippy, comments, and doc strings
Why VSCode for Rust?
- Rust Analyzer: Real-time error checking, autocomplete, type hints
- Integrated terminal: No more switching windows
- Git integration: Visual diffs, staging, commits
Setting up VSCode for Rust
You'll need to have
- Installed VSCode
- Installed Rust
- Installed the rust-analyzer extension
Opening our project
To make sure we're all at the same starting point, we'll recreate the project.
From MacOS terminal or Windows PowerShell (not git-bash):
# change to your projects folder
cd ~/projects
cargo new guessing_game
cd guessing_game
# check what the default branch name is
git branch
# if default branch is called `master`, rename it to `main`
git branch -m master main
# Add the `rand` crate to the project
cargo add rand
# start VS Code in the current directory
code .
or use File → Open Folder from VSCode and open ~/projects/guessing_game.
VSCode Features Demo
Side Panel
- Explorer
- single click and double click filenames
- split editor views
- Search,
- Source Control,
- Run and Debug,
- Extensions
- You should have
rust-analyzer, notrust!
- You should have
Integrated Terminal
View → Terminal,Terminal → New- You can have multiple terminals
- Same commands as before:
cargo run,cargo check
Rust Analyzer in Action
What you'll see:
- Red squiggles - Compiler errors
- Yellow squiggles - Warnings
- Hover tooltips - Type information
- Autocomplete - As you type suggestions
- Format on save - Automatic code formatting
Let's see it in action!
Completing Our Guessing Game
Restore Guessing Game
Replace the content in main.rs with the following:
use std::io;
use rand::Rng;
fn main() {
let secret_number = rand::rng().random_range(1..=100);
//println!("The secret number is: {secret_number}");
println!("Guess the number between 1 and 100!");
println!("Please input your guess.");
let mut guess = String::new();
io::stdin()
.read_line(&mut guess)
.expect("Failed to read line");
println!("You guessed: {}", guess);
}
Running from VSCode
You have different ways to run the program:
cargo runfrom terminal- Click the little
Runthat decorates abovefn main() {
VSCode Git Integration
Visual Git Features:
- Source Control panel - See changed files
- Diff view - Side-by-side comparisons
- Stage changes - Click the + button
- Commit - Write message and commit
Still use terminal for:
git status- Quick overviewgit log --oneline- Commit historygit push/git pull- Syncing
Create Git Commit
Let's use the visual interface to make our initi commit.
You can always do this via the integrated terminal instead.
Click the Source Control icon on the left panel.
Click + to stage each file or stage all changes.
Write the commit message: "Initial commit" and click Commit
Now you can see on the left pane that we have one commit.
Making it a real game:
- Remove the secret reveal - no cheating!
- Add a loop - keep playing until correct
- Compare numbers - too high? too low?
- Handle invalid input - what if they type "banana"?
But before we proceed, create a topic branch by
- clicking on
mainin the bottom left - Select
Create new branch... - Give it a name like
compare
Step 1: Comparing Numbers
First, we need to convert the guess to a number and compare:
#![allow(unused)] fn main() { // add at top of file after other `use` statements use std::cmp::Ordering; // Add this after reading input: let guess: u32 = guess.trim().parse().expect("Please enter a number!"); match guess.cmp(&secret_number) { Ordering::Less => println!("Too small!"), Ordering::Greater => println!("Too big!"), Ordering::Equal => println!("You win!"), } }
Now run the program to make sure it works.
If it does, then commit the changes to your topic branch.
Note how you can see the changes in the Source Control panel.
Merge Topic Branch
If you had a remote repo setup like on GitHub, you would then:
- push your topic branch to the remote
git push origin branch_name - ask someone to review and possible make changes and push those to the remote
But for now, we are just working locally.
git checkout main
# or use VSCode to switch to main
# merge changes from topic branch into main
git merge compare # replace 'compare' with your branch name
# delete your topic branch
git branch -d compare
Step 2: Adding the Loop
Now, we want to wrap the input/comparison in a loop.
But first create a new topic branch, e.g. loop
#![allow(unused)] fn main() { loop { println!("Please input your guess."); // ... input code ... match guess.cmp(&secret_number) { Ordering::Less => println!("Too small!"), Ordering::Greater => println!("Too big!"), Ordering::Equal => { println!("You win!"); break; // Exit the loop } } } }
You can indent multiple lines of code by selecting all the lines and then pressing TAB.
Try the code and if it works, commit, checkout main, merge topic branch and then delete topic branch.
Step 3: Handling Invalid Input
Run the program again and then try typing a word instead of a number.
Not great behavior, right?
Replace .expect() with proper error handling, but first create a topic branch.
#![allow(unused)] fn main() { let guess: u32 = match guess.trim().parse() { Ok(num) => num, Err(_) => { println!("Please enter a valid number!"); continue; // Skip to next loop iteration } }; }
Replace the relevant code, run and debug and do the git steps again.
You should end up on the main branch with all the changes merged and 4 commits.
Final Complete Game
use std::io;
use rand::Rng;
use std::cmp::Ordering;
fn main() {
let secret_number = rand::rng().random_range(1..=100);
//println!("The secret number is: {secret_number}");
println!("Guess the number between 1 and 100!");
loop {
println!("Please input your guess.");
let mut guess = String::new();
io::stdin()
.read_line(&mut guess)
.expect("Failed to read line");
println!("You guessed: {}", guess);
let guess: u32 = match guess.trim().parse() {
Ok(num) => num,
Err(_) => {
println!("Please enter a valid number!");
continue; // Skip to next loop iteration
}
};
match guess.cmp(&secret_number) {
Ordering::Less => println!("Too small!"),
Ordering::Greater => println!("Too big!"),
Ordering::Equal => {
println!("You win!");
break; // exit the loop
}
}
}
}Comments & Documentation Best Practices
What would happen if you came back to this program in a month?
Inline Comments (//)
- Explain why, not what the code does
- Bad:
// Create a random number - Good:
// Generate secret between 1-100 for balanced difficulty - If it's not clear what the code does you should edit the code!
Doc Comments (///)
- Document meaningful chunks of code like functions, structs, modules
- Show up in
cargo docand IDE tooltips
/// Prompts user for a guess and validates input
/// Returns the parsed number or continues loop on invalid input
fn get_user_guess() -> u32 {
// implementation...
}You can try putting a doc comment right before
fn main() {
The Better Comments extension
See it on VS Code marketplace
- Color-codes different types of comments in VSCode - let's paste it into
main.rsand see
// TODO: Add input validation here
// ! FIXME: This will panic on negative numbers
// ? Why does this work differently on Windows?
// * Important: This function assumes sorted inputHello VSCode and Hello Github Classroom!
Part 1: GitHub Classroom Set-up
Step 1: Accept the Assignment (One Person Per Group)
- Go here: https://classroom.github.com/a/XY-1jTAX
- Sign into GitHub if you aren't signed in, then select your name from the list
- Create or join a team:
- If you're first in your group: Click "Create a new team" and name it (e.g., "team-alice-bob")
- If teammate already started: Find and click on your team name
- Click "Accept this assignment"
- Click on repository URL to open it - it will look something like this:
https://github.com/cdsds210-fall25-b1/activity6-team-alice-bob
Step 2: Clone the Repository (Everyone)
Open a terminal and navigate to where you keep your projects (optional, but recommended for organization).
cd path/to/your/projects/
In the GitHub webpage for your group, click the green "code" button, and copy the link.
Then clone the repo in your terminal. Your clone command will look like one of these:
git clone https://github.com/cdsds210-fall25-b1/your-team-repo-name.git # HTTPS
Troubleshooting:
- If HTTPS asks for password: Use your GitHub username and a personal access token (not your GitHub password)
Step 3: Open in VSCode (Everyone)
cd your-team-repo-name
code .
You may see recommendations for a few extensions - do not install them. Carefully select extensions to install.
Step 4: VSCode Exploration
From within your project, open src/main.rs in the navigation sidebar.
Explore These Features:
- Hover over variables - What type information do you see?
- Type
println!and wait - Notice the autocomplete suggestions - Introduce a typo (like
printl!) - See the red squiggle error - Hover over
randto see definition pop up - Right-click on
rand- Try "Go to Definition" to jump to code - Open integrated terminal (
Ctrl+`orView -> Terminal) - Run
cargo runfrom the VSCode terminal
Part 2: Making contributions
Step 1: Make a plan as a team
Take a look at src/main.rs the repo as a group and identify two errors using VSCode hints and/or cargo check (you may need to fix one bug first in order to find the other). Then divide up these tasks among your team:
- Fixing the bugs (could be one person or split among two people)
- Adding some comments into
src/main.rsto explain how the code works - Editing the
README.mdfile to include a short summary of how you found the bugs, anything that was confusing or rewarding about this activity, or any other reflections
Step 2: Make individual branches
Make a branch that includes your name and what you're working on, eg. ryan-semicolon-bug-fix or kia-adding-comments
git checkout -b your-branch-name
Step 3: Fix your bug and/or add comments
Talk to each other if you need help!
Step 4: Commit and push
git add . # or add specific files
git commit -m "fix missing semicolon" # your own descriptive comment here
git push -u origin ryan-semicolon-bug-fix # your own branch name here
Step 5: Create a Pull Request
- Go to your team's GitHub repository in your browser
- Click the yellow "Compare & pull request" button (or go to "Pull requests" → "New pull request")
- Make sure the base is
mainand compare is your branch - Write a title like "Fix semicolon bug"
- Click "Create pull request"
Step 6: Review PRs and Merge
- Look at someone else's pull request (not your own!)
- Click "Files changed" to see their changes
- Leave feedback or request other changes if you want
- When you're ready, go to "Review changes" -> "Approve" -> "Submit review"
- Click "Merge pull request" -> "Confirm merge"
If you encounter "merge conflicts" try following these instructions.
Step 7: Is it working?
Run git checkout main and git pull when you're all done, and cargo run to see if your final code is working!
There's no "submit" button / step in GitHub Classroom - when you're done and your main branch is how you want it, you're done!
Wrap-up
What we've accomplished so far:
- Can now use shell, git, and rust all in one place (VSCode)
- We built a complete, functional game from scratch
- Started learning key Rust concepts: loops, matching, error handling
- We've practiced using GitHub Classroom - you'll use it for HW2!
Variables and Types in Rust
About This Module
This module covers Rust's type system and variable handling, including immutability by default, variable shadowing, numeric types, boolean operations, characters, and strings. Understanding these fundamentals is essential for all Rust programming.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
Pre-lecture Reflections
Before class, consider these questions:
- Why might immutable variables by default be beneficial for programming?
- What is the difference between variable shadowing and mutability?
- How do strongly typed languages like Rust prevent certain classes of bugs?
- What are the trade-offs between different integer sizes?
- Why might string handling be more complex than it initially appears?
Learning Objectives
By the end of this module, you should be able to:
- Understand Rust's immutability-by-default principle
- Use mutable variables when necessary
- Apply variable shadowing appropriately
- Choose appropriate numeric types for different use cases
- Work with boolean and bitwise operations
- Handle characters and strings properly in Rust
- Understand type conversion and casting in Rust
Variables are by default immutable!
Take a look at the following code.
Note: we'll use a red border to indicate that the code is expected to fail compilation.
#![allow(unused)] fn main() { let x = 3; x = x + 1; // <== error here }
Run it and you should get the following error.
Compiling playground v0.0.1 (/playground)
error[E0384]: cannot assign twice to immutable variable `x`
--> src/main.rs:4:1
|
3 | let x = 3;
| - first assignment to `x`
4 | x = x + 1; // <== error here
| ^^^^^^^^^ cannot assign twice to immutable variable
|
help: consider making this binding mutable
|
3 | let mut x = 3;
| +++
For more information about this error, try `rustc --explain E0384`.
error: could not compile `playground` (bin "playground") due to 1 previous error
The Rust compiler errors are quite helpful!
Use mut to make them mutable
#![allow(unused)] fn main() { // mutable variable let mut x = 3; x = x + 1; println!("x = {}", x); }
Assigning a different type to a mutable variable
What happens if you try to assign a different type to a mutable variable?
#![allow(unused)] fn main() { // mutable variable let mut x = 3; x = x + 1; println!("x = {}", x); x = 9.5; // what happens here?? println!("x = {}", x); }
Again, the Rust compiler error message is quite helpful!
Variable Shadowing
You can create a new variable with the same name as a previous variable!
fn main() { let solution = "4"; // This is a string // Create a new variable with same name and convert string to integer let solution : i32 = solution.parse() .expect("Not a number!"); // Create a third variable with the same name! let solution = solution * (solution - 1) / 2; println!("solution = {}",solution); // Create a fourth variable with the same name! let solution = "This is a string"; println!("solution = {}", solution); }
In this example, you can't get back to the original variable, although it stays in memory until it goes of out scope.
Question: why would you want to do this?
Question: Can you use
mutand avoid variable shadowing? Try it above.
Variable Shadowing and Scopes
Rust automatically deallocates variables when they go out of scope, such as when a program ends.
You can also use a block (bounded by {}) to limit the scope of a variable.
#![allow(unused)] fn main() { let x = 1; { // start of block scope let x = 2; // shadows outer x println!("{}", x); // prints `2` } // end of block scope println!("{}", x); // prints `1` again — outer `x` visible }
Basic Types: unsigned integers
unsigned integers: u8, u16, u32, u64, u128
usizeis the default unsigned integer size for your architecture
The number, e.g. 8, represents the number of bits in the type and the maximum value.
- So unsigned integers range from to .
| Unsigned Integer | Unsigned 8 bit binary |
|---|---|
| 0 | 00000000 |
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
Here's how you convert from binary to decimal.
Basic Types: unsigned integers - min and max values
Rust lets us print the minimum and maximum values of each type.
#![allow(unused)] fn main() { println!("U8 min is {} max is {}", u8::MIN, u8::MAX); println!("U16 min is {} max is {}", u16::MIN, u16::MAX); println!("U32 min is {} max is {}", u32::MIN, u32::MAX); println!("U64 min is {} max is {}", u64::MIN, u64::MAX); println!("U128 min is {} max is {}", u128::MIN, u128::MAX); println!("USIZE min is {} max is {}", usize::MIN, usize::MAX); }
Verify u8::MAX on your own.
Question: What is the
usizeon your machine?
Basic Types: signed integers
Similarly, there are these signed integer types.
signed integers: i8, i16, i32 (default), i64, i128,
isize is the default signed integer size for your architecture
- from to
Unsigned integers - min and max values
#![allow(unused)] fn main() { println!("I8 min is {} max is {}", i8::MIN, i8::MAX); println!("I16 min is {} max is {}", i16::MIN, i16::MAX); println!("I32 min is {} max is {}", i32::MIN, i32::MAX); println!("I64 min is {} max is {}", i64::MIN, i64::MAX); println!("I128 min is {} max is {}", i128::MIN, i128::MAX); println!("ISIZE min is {} max is {}", isize::MIN, isize::MAX); }
Signed integer representation
Signed integers are stored in two's complement format.
- if the number is positive, the first bit is 0
- if the number is negative, the first bit is 1
| Signed Integer | Signed 8 bit binary |
|---|---|
| 0 | 00000000 |
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
| -1 | 11111111 |
| -2 | 11111110 |
| -3 | 11111101 |
Here's how you convert from binary to decimal.
If the first bit is 0, the number is positive. If the first bit is 1, the number is negative.
To convert a negative number to decimal:
- take the sign of the first bit,
- flip all the bits and add 1 (only for negative numbers!)
Exercise: Try that for -1
Converting between signed and unsigned integers
If you need to convert, use the as operator:
#![allow(unused)] fn main() { let x: i8 = -1; let y: u8 = x as u8; println!("{}", y); }
Question: Can you explain the answer?
Why do we need ginormous i128 and u128?
They are useful for cryptography.
Don't use datatype sizes larger than you need.
Larger than architecture default generally takes more time.
i64 math operations might be twice as slow as i32 math.
Number literals
Rust lets us write number literals in a few different ways.
| Number literals | Example |
|---|---|
| Decimal (base 10) | 98_222 |
| Hex (base 16) | 0xff |
| Octal (base 8) | 0o77 |
| Binary (base 2) | 0b1111_0000 |
| Byte (u8 only) | b'A' |
#![allow(unused)] fn main() { let s1 = 2_55_i32; let s2 = 0xff; let s3 = 0o3_77; let s4 = 0b1111_1111; // print in decimal format println!("{} {} {} {}", s1, s2, s3, s4); // print in different bases println!("{} 0x{:X} 0o{:o} 0b{:b}", s1, s2, s3, s4); }
Be careful with math on ints
fn main() { let x : i16 = 13; let y : i32 = -17; // won't work without the conversion println!("{}", x * y); // will not work //println!("{}", (x as i32)* y); // this will work }
Basic Types: floats
There are two kinds: f32 and f64
What do these mean?
- This is the number of bits used in each type
- more complicated representation than ints (see wikipedia)
- There is talk about adding f128 to the language but it is not as useful as u128/i128.
fn main() { let x = 4.0; println!("x is of type {}", std::any::type_name_of_val(&x)); let z = 1.25; println!("z is of type {}", std::any::type_name_of_val(&z)); println!("{:.1}", x * z); }
Exercise: Try changing the type of
xtof32and see what happens:let x:f32 = 4.0;
Floats gotchas
Be careful with mixing f32 and f64 types.
You can't mix them without converting.
fn main() { let x:f32 = 4.0; println!("x is of type {}", std::any::type_name_of_val(&x)); let z:f64 = 1.25; println!("z is of type {}", std::any::type_name_of_val(&z)); println!("{:.1}", x * z); //println!("{:.1}", (x as f64) * z); // this will work }
Floats: min and max values
Rust lets us print the minimum and maximum values of each type.
#![allow(unused)] fn main() { println!("F32 min is {} max is {}", f32::MIN, f32::MAX); println!("F32 min is {:e} max is {:e}\n", f32::MIN, f32::MAX); println!("F64 min is {:e} max is {:e}", f64::MIN, f64::MAX); }
Exercise -- Integers and Floats
Create a program that:
- creates a
u8variablenwith value 77 - creates an
f32variablexwith value 1.25 - prints both numbers
- multiplies them and puts the results in an
f64variableresult - prints the result
Example output:
77
1.25
77 * 1.25 = 96.25
Get your code working here (or in your own editors) and then paste the result in Gradescope.
fn main() { }
More Basic Types
Let's look at:
- Booleans
- Characters
- Strings
Logical operators and bool
booluses one byte of memory
Question: Why is
boolone byte when all we need is one bit?
We can do logical operations on booleans.
#![allow(unused)] fn main() { let x = true; println!("x uses {} bits", std::mem::size_of_val(&x) * 8); let y: bool = false; println!("y uses {} bits\n", std::mem::size_of_val(&y) * 8); println!("{}", x && y); // logical and println!("{}", x || y); // logical or println!("{}", !y); // logical not }
Bitwise operators
There are also bitwise operators that look similar to logical operators but work on integers:
#![allow(unused)] fn main() { let x = 10; let y = 7; println!("{x:04b} & {y:04b} = {:04b}", x & y); // bitwise and println!("{x:04b} | {y:04b} = {:04b}", x | y); // bitwise or println!("!{y:04b} = {:04b} or {0}", !y); // bitwise not }
Bitwise 'not' and signed integers
#![allow(unused)] fn main() { let y = 7; println!("!{y:04b} = {:04b} or {0}", !y); // bitwise not }
What's going on with that last line?
y is I32, so let's display all 32 bits.
#![allow(unused)] fn main() { let y = 7; println!("{:032b}", y); }
So when we do !y we get the bitwise negation of y.
#![allow(unused)] fn main() { let y = 7; println!("{:032b}", !y); }
It's still interpreted as a signed integer.
#![allow(unused)] fn main() { let y = 7; println!("{}", !y); }
Bitwise Operators on Booleans?
It's a little sloppy but it works.
#![allow(unused)] fn main() { let x = true; println!("x is of type {}", std::any::type_name_of_val(&x)); println!("x uses {} bits", std::mem::size_of_val(&x) * 8); let y: bool = false; println!("y uses {} bits\n", std::mem::size_of_val(&y) * 8); // x and (not y) println!("{}", x & y); // bitwise and println!("{}", x | y); // bitwise or println!("{}", x ^ y); // bitwise xor }
Exercise -- Bitwise Operators on Integers
Create a program that:
- Creates an unsigned int
xwith value 12 and a signed intywith value -5 - Prints both numbers in binary format (use {:08b} for 8-bit display)
- Performs bitwise AND (&) and prints the result in binary
- Performs bitwise OR (|) and prints the result in binary
- Performs bitwise NOT (!) on both numbers and prints the results
Example output:
12: 00001100
-5: 11111011
12 & -5: 00001000
12 | -5: 11111101
!12: 11110011
!-5: 00000100
fn main() { }
Characters
chardefined via single quote, uses four bytes of memory (Unicode scalar value)- For a complete list of UTF-8 characters check https://www.fileformat.info/info/charset/UTF-8/list.htm
Note that on Mac, you can insert an emoji by typing
Control-Command-Spaceand then typing the emoji name, e.g. 😜.
On Windows, you can insert an emoji by typing
Windows-Key + .orWindows-Key + ;and then typing the emoji name, e.g. 😜.
#![allow(unused)] fn main() { let x: char = 'a'; println!("x is of type {}", std::any::type_name_of_val(&x)); println!("x uses {} bits", std::mem::size_of_val(&x) * 8); let y = '🚦'; println!("y is of type {}", std::any::type_name_of_val(&y)); println!("y uses {} bits", std::mem::size_of_val(&y) * 8); let z = '🦕'; println!("z is of type {}", std::any::type_name_of_val(&z)); println!("z uses {} bits", std::mem::size_of_val(&z) * 8); println!("{} {} {}", x, y, z); }
Strings and String Slices (&str)
In Rust, strings are not primitive types, but rather complex types built on top of other types.
String slices are immutable references to string data.
-
Stringis a growable, heap-allocated data structure -
&stris an immutable reference to a string slice -
Stringis a wrapper aroundVec<u8>(More onVeclater) -
&stris a wrapper around&[u8] -
string slice defined via double quotes (not so basic actually!)
String and string slice examples
fn main() { let s1 = "Hello! How are you, 🦕?"; // type is immutable borrowed reference to a string slice: `&str` let s2 : &str = "Καλημέρα από την Βοστώνη και την DS210"; // here we make the type explicit println!("{}", s1); println!("{}\n", s2); }
String and string slice examples
We have to explicitly convert a string slice to a string.
fn main() { // This doesn't work. You can't do String = &str let s3: String = "Does this work?"; // <== error here let s3: String = "Does this work?".to_string(); println!("{}", s3); }
Comment out the error lines and run the code to see what happens.
String and string slice examples
We can't index directly into a string slice, because it is a complex data structure.
Different characters can take up different numbers of bytes in UTF-8.
fn main() { let s4: String = String::from("How about this?"); println!("{}\n", s4); let s5: &str = &s3; println!("str reference to a String reference: {}\n", s5); // This won't work. You can't index directly into a string slice. Why??? println!("{}", s1[3]); // <== error here println!("{}", s2[3]); // <== error here // But you can index this way. println!("4th character of s1: {}", s1.chars().nth(3).unwrap()); println!("4th character of s2: {}", s2.chars().nth(3).unwrap()); println!("3rd character of s4: {}", s4.chars().nth(2).unwrap()); }
Comment out the error lines and run the code to see what happens.
Exercise -- String Slices
Create a program that:
- Creates a string slice containing your name
- Converts it to a String
- Gets the third character of your name using the
.chars().nth()method - Prints both the full name and the third character
Example output if your name is "Alice":
Alice
i
fn main() { }
Recap
- Variables are by default immutable
- Use
mutto make them mutable - Variable shadowing is a way to reuse the same name for a new variable
- Booleans are one byte of memory
- Bitwise operators work on integers
- Characters are four bytes of memory
- Strings are complex data structures
- String slices are immutable references to string data
Conditional Expressions and Flow Control in Rust
About This Module
This module covers Rust's conditional expressions, including if statements, if expressions,
and the unique ways Rust handles control flow. Understanding these concepts is fundamental
for writing effective Rust programs and leveraging Rust's expression-based syntax.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
Pre-lecture Reflections
Before class, consider these questions:
- What is the difference between statements and expressions in programming?
- How might expression-based syntax improve code readability and safety?
- What are the advantages of mandatory braces in conditional statements?
- How do different languages handle ternary operations?
- What role does type consistency play in conditional expressions?
Learning Objectives
By the end of this module, you should be able to:
- Use
ifstatements for conditional execution - Leverage
ifexpressions to assign values conditionally - Understand Rust's expression-based syntax
- Apply proper type consistency in conditional expressions
- Write clean, readable conditional code following Rust conventions
- Understand the differences between Rust and other languages' conditional syntax
An Aside -- Approach to Learning New Languages
Systematic Language Learning Framework:
When learning any new programming language, consider these key areas:
- Data Types: What types of variables and data structures are available?
- Functions: What is the syntax for defining and calling functions?
- Build System: How do you compile and run code?
- Control Flow: Syntax for conditionals, loops, and branching
- Code Organization: How to structure programs (structs, modules, etc.)
- Language-Specific Features: Unique aspects of the language
- Additional Considerations: I/O, external libraries, ecosystem
Basic if Statements
Syntax:
if condition {
DO-SOMETHING-HERE
} else {
DO-SOMETHING-ELSE-HERE
}elsepart optional- Compared to many C-like languages:
- no parentheses around
conditionneeded! - the braces mandatory
- no parentheses around
Example of if
Simple if statement.
fn main() { let x = 7; if x <= 15 { println!("x is not greater than 15"); } }
- parentheses optional around
condition-- try it with! - no semicolon after the
ifbraces
fn main() { let threshold = 5; if x <= threshold { println!("x is at most {}",threshold); } else { println!("x is greater than {}", threshold); } }
Using conditional expressions as values
In Python:
result = 100 if (x == 7) else 200
C++:
result = (x == 7) ? 100 : 200
Rust:
fn main() { let x = 4; let result = if x == 7 {100} else {200}; println!("{}",result); }
fn main() { // won't work: same type needed let x = 4; println!("{}",if x == 7 {100} else {1.2}); }
- blocks can be more complicated
- last expression counts (no semicolon after)
- But please don't write this just because you can
#![allow(unused)] fn main() { let x = 4; let z = if x == 4 { let t = x * x; t + 1 } else { x + 1 }; println!("{}",z); }
Write this instead:
#![allow(unused)] fn main() { let x = 4; let z; if x == 4 { z = x*x+1 } else { z = x+1}; println!("{}", z) }
Obscure Code Competition Winner
A winner of the most obscure code competition (https://www.ioccc.org/)
What does this program do?
#include <stdio.h>
#define N(a) "%"#a"$hhn"
#define O(a,b) "%10$"#a"d"N(b)
#define U "%10$.*37$d"
#define G(a) "%"#a"$s"
#define H(a,b) G(a)G(b)
#define T(a) a a
#define s(a) T(a)T(a)
#define A(a) s(a)T(a)a
#define n(a) A(a)a
#define D(a) n(a)A(a)
#define C(a) D(a)a
#define R C(C(N(12)G(12)))
#define o(a,b,c) C(H(a,a))D(G(a))C(H(b,b)G(b))n(G(b))O(32,c)R
#define SS O(78,55)R "\n\033[2J\n%26$s";
#define E(a,b,c,d) H(a,b)G(c)O(253,11)R G(11)O(255,11)R H(11,d)N(d)O(253,35)R
#define S(a,b) O(254,11)H(a,b)N(68)R G(68)O(255,68)N(12)H(12,68)G(67)N(67)
char* fmt = O(10,39)N(40)N(41)N(42)N(43)N(66)N(69)N(24)O(22,65)O(5,70)O(8,44)N(
45)N(46)N (47)N(48)N( 49)N( 50)N( 51)N(52)N(53 )O( 28,
54)O(5, 55) O(2, 56)O(3,57)O( 4,58 )O(13, 73)O(4,
71 )N( 72)O (20,59 )N(60)N(61)N( 62)N (63)N (64)R R
E(1,2, 3,13 )E(4, 5,6,13)E(7,8,9 ,13)E(1,4 ,7,13)E
(2,5,8, 13)E( 3,6,9,13)E(1,5, 9,13)E(3 ,5,7,13
)E(14,15, 16,23) E(17,18,19,23)E( 20, 21, 22,23)E
(14,17,20,23)E(15, 18,21,23)E(16,19, 22 ,23)E( 14, 18,
22,23)E(16,18,20, 23)R U O(255 ,38)R G ( 38)O( 255,36)
R H(13,23)O(255, 11)R H(11,36) O(254 ,36) R G( 36 ) O(
255,36)R S(1,14 )S(2,15)S(3, 16)S(4, 17 )S (5, 18)S(6,
19)S(7,20)S(8, 21)S(9 ,22)H(13,23 )H(36, 67 )N(11)R
G(11)""O(255, 25 )R s(C(G(11) ))n (G( 11) )G(
11)N(54)R C( "aa") s(A( G(25)))T (G(25))N (69)R o
(14,1,26)o( 15, 2, 27)o (16,3,28 )o( 17,4, 29)o(18
,5,30)o(19 ,6,31)o( 20,7,32)o (21,8,33)o (22 ,9,
34)n(C(U) )N( 68)R H( 36,13)G(23) N(11)R C(D( G(11)))
D(G(11))G(68)N(68)R G(68)O(49,35)R H(13,23)G(67)N(11)R C(H(11,11)G(
11))A(G(11))C(H(36,36)G(36))s(G(36))O(32,58)R C(D(G(36)))A(G(36))SS
#define arg d+6,d+8,d+10,d+12,d+14,d+16,d+18,d+20,d+22,0,d+46,d+52,d+48,d+24,d\
+26,d+28,d+30,d+32,d+34,d+36,d+38,d+40,d+50,(scanf(d+126,d+4),d+(6\
-2)+18*(1-d[2]%2)+d[4]*2),d,d+66,d+68,d+70, d+78,d+80,d+82,d+90,d+\
92,d+94,d+97,d+54,d[2],d+2,d+71,d+77,d+83,d+89,d+95,d+72,d+73,d+74\
,d+75,d+76,d+84,d+85,d+86,d+87,d+88,d+100,d+101,d+96,d+102,d+99,d+\
67,d+69,d+79,d+81,d+91,d+93,d+98,d+103,d+58,d+60,d+98,d+126,d+127,\
d+128,d+129
char d[538] = {1,0,10,0,10};
int main() {
while(*d) printf(fmt, arg);
}
Best Practices
Formatting and Style:
- Use consistent indentation (4 spaces)
- Keep conditions readable - use parentheses for clarity when needed
- Prefer early returns in functions to reduce nesting
- Use
else iffor multiple conditions rather than nestedif
Example of Good Style:
fn classify_temperature(temp: f64) -> &'static str { if temp > 30.0 { "Hot" } else if temp > 20.0 { "Warm" } else if temp > 10.0 { "Cool" } else { "Cold" } } fn main() { println!("{}", classify_temperature(35.0)); println!("{}", classify_temperature(25.0)); println!("{}", classify_temperature(15.0)); println!("{}", classify_temperature(5.0)); }
Exercise
Write a function that takes a number and returns a string that says whether it is positive, negative, or zero.
Example output:
10 is positive
-5 is negative
0 is zero
// Your code here
Functions in Rust
About This Module
This module covers Rust function syntax, return values, parameters, and the unit type. Functions are fundamental building blocks in Rust programming, and understanding their syntax and behavior is essential for writing well-structured Rust programs.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 3.3: Functions
- Chapter 4.1: What Is Ownership? - Introduction only
Pre-lecture Reflections
Before class, consider these questions:
- How do functions help organize and structure code?
- What are the benefits of explicit type annotations in function signatures?
- How do return values differ from side effects in functions?
- What is the difference between expressions and statements in function bodies?
- How might Rust's approach to functions differ from other languages you know?
Learning Objectives
By the end of this module, you should be able to:
- Define functions with proper Rust syntax
- Understand parameter types and return type annotations
- Use both explicit
returnstatements and implicit returns - Work with functions that return no value (unit type)
- Apply best practices for function design and readability
- Understand the difference between expressions and statements in function bodies
Function Syntax
Syntax:
fn function_name(argname_1:type_1,argname_2:type_2) -> type_ret {
DO-SOMETHING-HERE-AND-RETURN-A-VALUE
}- No need to write "return x * y"
- Last expression is returned
- No semicolon after the last expression
fn multiply(x:i32, y:i32) -> i32 { // note: no need to write "return x * y" x * y } fn main() { println!("{}", multiply(10,20)) }
Exercise: Try putting a semicolon after the last expression. What happens?
Functions returns
- But if you add a return then you need a semicolon
- unless it is the last statement in the function
- Recommend using returns and add semicolons everywhere.
- It's easier to read.
fn and(p:bool, q:bool, r:bool) -> bool { if !p { println!("p is false"); return false; } if !q { println!("q is false"); return false; } println!("r is {}", r); r // return r without the semicolon also works here } fn main() { println!("{}", and(true,false,true)) }
Functions: returning no value
How: skip the type of returned value part
fn say_hello(who:&str) { println!("Hello, {}!",who); } fn main() { say_hello("world"); say_hello("Boston"); say_hello("DS210"); }
Nothing returned equivalent to the unit type, ()
fn say_good_night(who:&str) -> () { println!("Good night {}",who); } fn main() { say_good_night("room"); say_good_night("moon"); let z = say_good_night("cow jumping over the moon"); println!("The function returned {:?}", z) }
Unit Type Characteristics:
- Empty tuple:
() - Zero size: Takes no memory
- Default return: When no value is explicitly returned
- Side effects only: Functions that only perform actions (printing, file I/O, etc.)
Parameter Handling
Multiple Parameters:
#![allow(unused)] fn main() { fn calculate_area(length: f64, width: f64) -> f64 { length * width } fn greet_person(first_name: &str, last_name: &str, age: u32) { println!("Hello, {} {}! You are {} years old.", first_name, last_name, age); } }
Parameter Types:
- Ownership: Parameters can take ownership (
String) - References: Parameters can borrow (
&str,&i32) - Primitive types: Copied by default (
i32,bool,f64)
Function Design Principles
Single Responsibility:
// Good: Single purpose fn calculate_tax(price: f64, tax_rate: f64) -> f64 { price * tax_rate } // Good: Clear separation of concerns fn format_currency(amount: f64) -> String { format!("${:.2}", amount) } fn display_total(subtotal: f64, tax_rate: f64) { let tax = calculate_tax(subtotal, tax_rate); let total = subtotal + tax; println!("Total: {}", format_currency(total)); } fn main() { display_total(100.0, 0.08); }
Pure Functions vs. Side Effects:
#![allow(unused)] fn main() { // Pure function: No side effects, deterministic fn add(x: i32, y: i32) -> i32 { x + y } // Function with side effects: Prints to console fn add_and_print(x: i32, y: i32) -> i32 { let result = x + y; println!("{} + {} = {}", x, y, result); result } }
Common Patterns
Validation Functions:
#![allow(unused)] fn main() { fn is_valid_age(age: i32) -> bool { age >= 0 && age <= 150 } fn is_valid_email(email: &str) -> bool { email.contains('@') && email.contains('.') } }
Conversion Functions:
#![allow(unused)] fn main() { fn celsius_to_fahrenheit(celsius: f64) -> f64 { celsius * 9.0 / 5.0 + 32.0 } fn fahrenheit_to_celsius(fahrenheit: f64) -> f64 { (fahrenheit - 32.0) * 5.0 / 9.0 } }
Helper Functions:
#![allow(unused)] fn main() { fn get_absolute_value(x: i32) -> i32 { if x < 0 { -x } else { x } } fn max_of_three(a: i32, b: i32, c: i32) -> i32 { if a >= b && a >= c { a } else if b >= c { b } else { c } } }
Function Naming Conventions
Rust Naming Guidelines:
- snake_case: For function names
- Descriptive names: Clear indication of purpose
- Verb phrases: For functions that perform actions
- Predicate functions: Start with
is_,has_,can_
Examples:
#![allow(unused)] fn main() { fn calculate_distance(x1: f64, y1: f64, x2: f64, y2: f64) -> f64 { /* ... */ } fn is_prime(n: u32) -> bool { /* ... */ } fn has_permission(user: &str, resource: &str) -> bool { /* ... */ } fn can_access(user_level: u32, required_level: u32) -> bool { /* ... */ } }
Exercise
Write a function called greet_user that takes a name and a time of day (morning, afternoon, evening) as parameters and returns an appropriate greeting string.
The function should:
- Take two parameters:
name: &strandtime: &str - Return a
Stringwith a customized greeting - Follow Rust naming conventions
- Use proper parameter types
- Include error handling for invalid times
Example output:
Good evening, Dumbledore!
Hint: You can format the string using the format! macro, which uses the same syntax as println!.
// Returns a String
format!("Good morning, {}!", name)// Your code here
Loops and Arrays in Rust
About This Module
This module covers Rust's loop constructs (for, while, loop) and array data structures.
Understanding loops and arrays is essential for processing collections of data and implementing
algorithms in Rust.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 3.5: Control Flow - Focus on loops
- Chapter 4.1: What Is Ownership? - Arrays and ownership
- Chapter 8.1: Storing Lists of Values with Vectors - Introduction only
Pre-lecture Reflections
Before class, consider these questions:
- What are the different types of loops and when would you use each?
- How do arrays differ from more flexible data structures like vectors?
- What are the advantages of fixed-size arrays?
- How do ranges work in iteration and what are their bounds?
- When might you need labeled breaks and continues in nested loops?
Learning Objectives
By the end of this module, you should be able to:
- Use
forloops with ranges and collections - Work with
whileloops for conditional iteration - Understand
loopfor infinite loops with explicit breaks - Create and manipulate arrays in Rust
- Use
breakandcontinuestatements effectively - Apply loop labels for complex control flow
- Understand array properties and limitations
For Loops and Ranges
Loops: for
Usage: loop over a range or collection
A range is (start..end), e.g. (1..5), where the index will vary as
Unless you use the notation (start..=end), in which case the index will vary as
#![allow(unused)] fn main() { // parentheses on the range are optional unless calling a method e.g. `.rev()` // on the range for i in 1..5 { println!("{}",i); } }
#![allow(unused)] fn main() { // inclusive range for i in 1..=5 { println!("{}",i); } }
#![allow(unused)] fn main() { // reverse order. we need parentheses! for i in (1..5).rev() { println!("{}",i) } }
#![allow(unused)] fn main() { // every other element for i in (1..5).step_by(2) { println!("{}",i); } }
#![allow(unused)] fn main() { println!("And now for the reverse"); for i in (1..5).step_by(2).rev() { println!("{}",i) } }
#![allow(unused)] fn main() { println!("But...."); for i in (1..5).rev().step_by(2) { println!("{}",i); } }
Arrays and for over an array
- Arrays in Rust are of fixed length (we'll learn about more flexible
Veclater) - All elements of the same type
- You can not add or remove elements from an array (but you can change its value)
- Python does not have arrays natively.
What's the closest thing in native python?
#![allow(unused)] fn main() { // simplest definition // compiler guessing element type to be i32 // indexing starts at 0 let mut arr = [1,7,2,5,2]; arr[1] = 13; println!("{} {}",arr[0],arr[1]); }
#![allow(unused)] fn main() { let mut arr = [1,7,2,5,2]; // array supports sorting arr.sort(); // loop over the array for x in arr { println!("{}",x); } }
#![allow(unused)] fn main() { // create array of given length // and fill it with a specific value let arr2 = [15;3]; for x in arr2 { print!("{} ",x); // notice print! instead of println! } }
#![allow(unused)] fn main() { // with type definition and shorthand to repeat values let arr3 : [u8;3] = [15;3]; for x in arr3 { print!("{} ",x); } println!(); println!("arr3[2] is {}", arr3[2]); }
#![allow(unused)] fn main() { let arr3 : [u8;3] = [15;3]; // get the length println!("{}",arr3.len()) }
Loops: while
#![allow(unused)] fn main() { let mut number = 3; while number != 0 { println!("{number}!"); number -= 1; } println!("LIFT OFF!!!"); }
Infinite loop: loop
loop {
// DO SOMETHING HERE
}Need to use break to jump out of the loop!
#![allow(unused)] fn main() { let mut x = 1; loop { if (x + 1) * (x + 1) >= 250 {break;} x += 1; } println!("{}",x) }
loopcan return a value!breakcan act likereturn
#![allow(unused)] fn main() { let mut x = 1; let y = loop { if x * x >= 250 {break x - 1;} x += 1; }; println!("{}",y) }
continueto skip the rest of the loop body and start the next iteration
#![allow(unused)] fn main() { // loop keyword similar to while (True) in Python // break and continue keywords behave as you would expect let mut x = 1; let result = loop { // you can capture a return value if x == 5 { x = x+1; continue; // skip the rest of this loop body and start the next iteration } println!("X is {}", x); x = x + 1; if x==10 { break x*2; // break with a return value } }; println!("Result is {}", result); }
Advanced break and continue
- work in all loops
break: terminate the execution- can return a value in
loop
- can return a value in
continue: terminate this iteration and jump to the next one- in
while, the condition will be checked - in
for, there may be no next iteration breakandcontinuecan use labels
- in
#![allow(unused)] fn main() { for i in 1..=10 { if i % 3 != 0 {continue;} println!("{}",i); }; }
You can also label loops to target with continue and break.
#![allow(unused)] fn main() { let mut x = 1; 'outer_loop: loop { println!("Hi outer loop"); 'inner_loop: loop { println!("Hi inner loop"); x = x + 1; if x % 3 != 0 { continue 'outer_loop; // skip the rest of the outer loop body and start the next iteration } println!("In the middle"); if x >= 10 { break 'outer_loop; // break the outer loop } println!("X is {}", x); } println!("In the end"); }; println!("Managed to escape! :-) with x {}", x); }
#![allow(unused)] fn main() { let mut x = 1; 'outer_loop: loop { println!("Hi outer loop"); 'inner_loop: loop { println!("Hi inner loop"); x = x + 1; if x % 3 != 0 { break 'inner_loop; // break the inner loop, continue the outer loop } println!("In the middle"); if x >= 10 { break 'outer_loop; // break the outer loop } println!("X is {}", x); } println!("In the end"); }; println!("Managed to escape! :-) with x {}", x); }
#![allow(unused)] fn main() { let x = 'outer_loop: loop { loop { break 'outer_loop 1234;} }; println!("{}",x); }
Loop Selection Guidelines
When to Use Each Loop Type:
For Loops:
- Known range: Iterating over ranges or collections
- Collection processing: Working with arrays, vectors, etc.
- Counter-based iteration: When you need an index
While Loops:
- Condition-based: Continue until some condition changes
- Unknown iteration count: Don't know how many times to loop
- Input validation: Keep asking until valid input
Loop (Infinite):
- Event loops: Server applications, game loops
- Breaking on complex conditions: When simple while condition isn't sufficient
- Returning values: When loop needs to compute and return a result
Exercise
Here's an exam question from a previous semester. Analyze the code without any assistance to practice your skills for the next exam.
You are given the following Rust code
let mut x = 1;
'outer_loop: loop {
'inner_loop: loop {
x = x + 1;
if x % 4 != 0 {
continue 'outer_loop;
}
if x > 11 {
break 'outer_loop;
}
}
};
println!("Managed to escape! :-) with x {}", x);What is the value of x printed by the println! statement at the end?
Explain your answer.
Tuples in Rust
About This Module
This module covers Rust's tuple data structure, which allows grouping multiple values of different types into a single compound value. Tuples are fundamental for returning multiple values from functions and organizing related data.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 3.2: Data Types - Focus on tuples subsection
- Chapter 6: Enums and Pattern Matching - Overview only
- Chapter 18.3: Pattern Syntax - Introduction only
Pre-lecture Reflections
Before class, consider these questions:
- What advantages do tuples provide over separate variables?
- How might tuples be useful for function return values?
- What are the trade-offs between tuples and structs?
- How does pattern matching with tuples improve code readability?
- When would you choose tuples versus arrays for grouping data?
Learning Objectives
By the end of this module, you should be able to:
- Create and use tuples with different data types
- Access tuple elements using indexing and destructuring
- Apply pattern matching with tuples
- Use tuples for multiple return values from functions
- Understand when to use tuples versus other data structures
- Work with nested tuples and complex tuple patterns
What Are Tuples?
A general-purpose data structure that can hold multiple values of different types.
- Syntax:
(value_1,value_2,value_3) - Type:
(type_1,type_2,type_3)
#![allow(unused)] fn main() { let mut tuple = (1,1.1); let mut tuple2: (i32,f64) = (1,1.1); // type annotation is optional in this case println!("tuple: {:?}, tuple2: {:?}", tuple, tuple2); }
#![allow(unused)] fn main() { let another = ("abc","def","ghi"); println!("another: {:?}", another); }
#![allow(unused)] fn main() { let yet_another: (u8,u32) = (255,4_000_000_000); println!("yet_another: {:?}", yet_another); }
Aside: Debug formatting
Look carefully at the variable formatting:
fn main() { let student = ("Alice", 88.5, 92.0, 85.5); println!("student: {:?}", student); // ^^ }
Rust uses the {:?} format specifier to print the variable in a debug format.
We'll talk more about what this means, but for now, just know that's often a good tool to use when debugging.
Accessing Tuple Elements
There are two ways to access tuple elements:
1. Accessing elements via index (0 based)
#![allow(unused)] fn main() { let mut tuple = (1,1.1); println!("({}, {})", tuple.0, tuple.1); tuple.0 = 2; println!("({}, {})",tuple.0,tuple.1); println!("Tuple is {:?}", tuple); }
2. Pattern matching and deconstructing
fn main() { let tuple = (1,1.1); let (a, b) = tuple; println!("a = {}, b = {}",a,b); }
Best Practices
When to Use Tuples:
- Small, related data: 2-4 related values
- Temporary grouping: Short-lived data combinations
- Function returns: Multiple return values
- Pattern matching: When destructuring is useful
When to Avoid Tuples:
- Many elements: More than 4-5 elements becomes unwieldy
- Complex data: When you need named fields for clarity
- Long-term storage: When data structure will evolve
Style Guidelines:
// Good: Clear, concise
let (width, height) = get_dimensions();
// Good: Descriptive destructuring
let (min_temp, max_temp, avg_temp) = analyze_temperatures(&data);
// Avoid: Too many elements
// let config = (true, false, 42, 3.14, "test", 100, false); // Hard to read
// Avoid: Unclear meaning
// let data = (42, 13); // What do these numbers represent?In-Class Exercise
Exercise: Student Grade Tracker
Create a program that tracks student information and calculates grade statistics. Work through the following steps:
-
Create a tuple to store a student's name (String) and three test scores (f64, f64, f64)
-
Calculate the average of the three test scores and create a new tuple that includes the student's name and average grade
-
Use pattern matching to destructure and display the student's name and average in a readable format
-
Bonus: Create multiple student tuples and use pattern matching to find students with averages above 85.0
fn main() { // Step 1: Create a student tuple (name, score1, score2, score3) let student1 = ... // Step 2: Deconstruct the tuple into separate variables let ... // Step 2: Calculate average and create new tuple (name, average) let average = ... let student_grade = ... // Step 3: Deconstruct student_grade into variables // student_name and avg_grade let ... println!("Student: {}, Average: {:.1}", student_name, avg_grade); }
Expected Output:
Student: Alice, Average: 88.7
Recap
- Tuples are a general-purpose data structure that can hold multiple values of different types
- We can access tuple elements via index or by pattern matching and deconstructing
- Pattern matching is a powerful tool for working with tuples
- Tuples are often used for multiple return values from functions
Enums and Pattern Matching in Rust
About This Module
This module introduces Rust's enum (enumeration) types and pattern matching with match
and if let. Enums allow you to define custom types by enumerating possible variants,
and pattern matching provides powerful control flow based on enum values.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 6.1: Defining an Enum
- Chapter 6.2: The match Control Flow Construct
- Chapter 6.3: Concise Control Flow with if let
Pre-lecture Reflections
Before class, consider these questions:
- How do enums help make code more expressive and type-safe?
- What advantages does pattern matching provide over traditional if-else chains?
- How might enums be useful for error handling in programs?
- What is the difference between enums in Rust and in other languages you know?
- When would you use
matchversusif letfor pattern matching?
Learning Objectives
By the end of this module, you should be able to:
- Define custom enum types with variants
- Create instances of enum variants
- Use
matchexpressions for exhaustive pattern matching - Apply
if letfor simplified pattern matching - Store data in enum variants
- Understand memory layout of enums
- Use the
#[derive(Debug)]attribute for enum display
Enums
enum is short for "enumeration" and allows you to define a type by enumerating
its possible variants.
The type you define can only take on one of the variants you have defined.
Allows you to encode meaning along with data.
Pattern matching using match and if let allows you to run different code depending on the value of the enum.
Python doesn't have native support for
enum, but it does have anenummodule that let's do something similar by subclassing anEnumclass.
Basic Enums
Let's start with a simple example:
// define the enum and its variants enum Direction { North, // <---- enum _variant_ East, South, West, SouthWest, } fn main() { // create instances of the enum variants let dir_1 = Direction::North; // dir is inferred to be of type Direction let dir_2: Direction = Direction::South; // dir_2 is explicitly of type Direction }
The enum declaration is defining our new type, so now a type called Direction is in scope,
similar to i32, f64, bool, etc., but it instances can only be one of the variants we have defined.
The let declarations are creating instances of the Direction type.
Aside: Rust Naming Conventions
Rust has a set of naming conventions that are used to make the code more readable and consistent.
You should follow these conventions when naming your enums, variants, functions, and other items in your code.
| Item | Convention |
|---|---|
| Crates | snake_case (but prefer single word) |
| Modules | snake_case |
| Types (e.g. enums) | UpperCamelCase |
| Traits | UpperCamelCase |
| Enum variants | UpperCamelCase |
| Functions | snake_case |
| Methods | snake_case |
| General constructors | new or with_more_details |
| Conversion constructors | from_some_other_type |
| Local variables | snake_case |
| Static variables | SCREAMING_SNAKE_CASE |
| Constant variables | SCREAMING_SNAKE_CASE |
| Type parameters | concise UpperCamelCase, usually single uppercase letter: T |
| Lifetimes | short, lowercase: 'a |
Using "use" as a shortcut
You can bring the variants into scope using use statements.
// define the enum and its variants enum Direction { North, East, South, West, SouthWest, } // Bring the variant `East` into scope use Direction::East; fn main() { // we didn't have to specify "Direction::" let dir_3 = East; }
Using "use" as a shortcut
You can bring multiple variants into scope using use statements.
// define the enum and its variants enum Direction { North, East, South, West, SouthWest, } // Bringing two options into the current scope use Direction::{East,West}; fn main() { let dir_4 = West; }
Using "use" as a shortcut
You can bring all the variants into scope using use statements.
enum Direction { North, East, South, West, } // Bringing all options in use Direction::*; fn main() { let dir_5 = South; }
Question: Why might we not always want to bring all the variants into scope?
Name clashes
use <enum_name>::*; will bring all the variants into scope, but if you have a variable with the same name as a variant, it will clash.
Uncomment the use Prohibited::*; line to see the error.
enum Prohibited { MyVar, YourVar, } // what happens if we bring all the variants into scope? // use Prohibited::*; fn main() { let MyVar = "my string"; let another_var = Prohibited::MyVar; println!("{MyVar}"); }
Aside: Quick Recap on Member Access
Different data structures have different ways of accessing their members.
fn main() { // Accessing an element of an array let arr = [1, 2, 3]; println!("{}", arr[0]); // Accessing an element of a tuple let tuple = (1, 2, 3); println!("{}", tuple.0); let (a, b, c) = tuple; println!("{}, {}, {}", a, b, c); // Accessing a variant of an enum enum Direction { North, East, South, West, } let dir = Direction::East; }
Using enums as parameters
We can also define a function that takes our new type as an argument.
enum Direction { North, East, South, West, } fn turn(dir: Direction) { return; } // this function doesn't do anything fn main() { let dir = Direction::East; turn(dir); }
Control Flow with match
Enums: Control Flow with match
The match statement is used to control flow based on the value of an enum.
enum Direction { North, East, South, West, } fn main() { let dir = Direction::East; // print the direction match dir { Direction::North => println!("N"), Direction::South => println!("S"), Direction::West => { // can do more than one thing println!("Go west!"); println!("W") } Direction::East => println!("E"), }; }
Take a close look at the match syntax.
Covering all variants with match
match is exhaustive, so we must cover all the variants.
// Won't compile enum Direction { North, East, South, West, } fn main() { let dir_2: Direction = Direction::South; // won't work match dir_2 { Direction::North => println!("N"), Direction::South => println!("S"), // East and West not covered }; }
But there is a way to match anything left.
Covering all variants with match
There's a special pattern, _, that matches anything.
enum Direction { North, East, South, West, } fn main() { let dir_2: Direction = Direction::North; match dir_2 { Direction::North => println!("N"), Direction::South => println!("S"), // match anything left _ => (), // covers all the other variants but doesn't do anything } }
Covering all variants with match
WARNING!!
The _ pattern has to be the last pattern in the match statement.
enum Direction { North, East, South, West, } fn main() { let dir_2: Direction = Direction::North; match dir_2 { _ => println!("anything else"), // will never get here!! Direction::North => println!("N"), Direction::South => println!("S"), } }
Recap of match
- Type of a switch statement like in C/C++ (Python doesn't have an equivalent)
- Must be exhaustive though there is a way to specify default (
_ =>)
Putting Data in an Enum Variant
- Each variant can come with additional information
- Let's put a few things together with an example
#[derive(Debug)] // allows us to print the enum by having Rust automatically // implement a Debug trait (more later) enum DivisionResult { Ok(f32), // This variant has an associated value of type f32 DivisionByZero, } // Return a DivisionResult that handles the case where the division is by zero. fn divide(x:f32, y:f32) -> DivisionResult { if y == 0.0 { return DivisionResult::DivisionByZero; } else { return DivisionResult::Ok(x / y); // Prove a value with the variant } } fn show_result(result: DivisionResult) { match result { DivisionResult::Ok(result) => println!("the result is {}",result), DivisionResult::DivisionByZero => println!("noooooo!!!!"), } } fn main() { let (a,b) = (9.0,3.0); // this is just short hand for let a = 9.0; let b = 3.0; println!("Dividing 9 by 3:"); show_result(divide(a,b)); println!("Dividing 6 by 0:"); show_result(divide(6.0,0.0)); // we can also call `divide`, store the result and print it let z = divide(5.0, 4.0); println!("The result of 5.0 / 4.0 is {:?}", z); }
Variants with multiple values
We can have more than one associated value in a variant.
enum DivisionResultWithRemainder { Ok(u32,u32), // Store the result of the integer division and the remainder DivisionByZero, } fn divide_with_remainder(x:u32, y:u32) -> DivisionResultWithRemainder { if y == 0 { DivisionResultWithRemainder::DivisionByZero } else { // Return the integer division and the remainder DivisionResultWithRemainder::Ok(x / y, x % y) } } fn main() { let (a,b) = (9,4); println!("Dividing 9 by 4:"); match divide_with_remainder(a,b) { DivisionResultWithRemainder::Ok(result,remainder) => { println!("the result is {} with a remainder of {}",result,remainder); } DivisionResultWithRemainder::DivisionByZero => println!("noooooo!!!!"), }; }
Getting the value out of an enum variant
We can use match to get the value out of an enum variant.
#[derive(Debug)] enum Message { Quit, Move { x: i32, y: i32 }, Write(String), ChangeColor(i32, i32, i32), } fn main() { let msg = Message::Write(String::from("Hello, world!")); // Extract values using match match msg { Message::Quit => println!("Quit message"), Message::Move { x, y } => println!("Move to ({}, {})", x, y), Message::Write(text) => println!("Write: {}", text), Message::ChangeColor(r, g, b) => println!("Color: RGB({}, {}, {})", r, g, b), } // Using if let for single variant extraction let msg2 = Message::Move { x: 10, y: 20 }; if let Message::Move { x, y } = msg2 { println!("Extracted coordinates: x={}, y={}", x, y); } }
A Note on the Memory Size of Enums
The size of the enum is related to the size of its largest variant, not the sum of the sizes.
Also stores a discriminant (tag) to identify which variant is stored.
use std::mem; enum SuperSimpleEnum { First, Second, Third } enum SimpleEnum { A, // No data B(i32), // Contains an i32 (4 bytes) C(i32, i32), // Contains two i32s (8 bytes) D(i64) // Contains an i64 (8 bytes) } fn main() { println!("Size of SuperSimpleEnum: {} bytes\n", mem::size_of::<SuperSimpleEnum>()); println!("Size of SimpleEnum: {} bytes\n", mem::size_of::<SimpleEnum>()); println!("Size of i32: {} bytes", mem::size_of::<i32>()); println!("Size of (i32, i32): {} bytes", mem::size_of::<(i32, i32)>()); println!("Size of (i64): {} bytes", mem::size_of::<(i64)>()); }
For variant C, it's possible that the compiler is aligning each i32 on an 8-byte boundary,
so the total size is 16 bytes. Common for modern 64-bit machines.
More on memory size of enums
use std::mem::size_of; enum Message { Quit, ChangeColor(u8, u8, u8), Move { x: i32, y: i32 }, Write(String), } enum Status { Pending, InProgress, Completed, Failed, } fn main() { // General case (on a 64-bit machine) println!("Size of Message: {} bytes", size_of::<Message>()); // C-like enum println!("Size of Status: {} bytes", size_of::<Status>()); // Prints 1 // References are addresses which are 64-bit (8 bytes) println!("Size of &i32: {} bytes", size_of::<&i32>()); // Prints 8 }
Displaying enums
By default Rust doesn't know how to display a new enum type.
Here we try to debug print the Direction enum.
// won't compile enum Direction { North, East, South, West, } fn main() { let dir = Direction::North; println!("{:?}",dir); }
Displaying enums (#[derive(Debug)])
Adding the #[derive(Debug)] attribute to the enum definition allows Rust to automatically implement the Debug trait.
#[derive(Debug)] enum Direction { North, East, South, West, } use Direction::*; fn main() { let dir = Direction::North; println!("{:?}",dir); }
match as expression
The result of a match can be used as an expression.
Each branch (arm) returns a value.
#[derive(Debug)] enum Direction { North, East, South, West, } use Direction::*; fn main() { // swap east and west let mut dir_4 = North; println!("{:?}", dir_4); dir_4 = match dir_4 { East => West, West => { println!("Switching West to East"); East } // variable mathching anything else _ => West, }; println!("{:?}", dir_4); }
Simplifying matching
Consider the following example (in which we want to use just one branch):
#[derive(Debug)] enum DivisionResult { Ok(u32,u32), DivisionByZero, } fn divide(x:u32, y:u32) -> DivisionResult { if y == 0 { DivisionResult::DivisionByZero } else { DivisionResult::Ok(x / y, x % y) } } fn main() { match divide(8,3) { DivisionResult::Ok(result,remainder) => println!("{} (remainder {})",result,remainder), _ => (), // <--- how to avoid this? }; }
This is a common enough pattern that Rust provides a shortcut for it.
Simplified matching with if let
if let allows for matching just one branch (arm)
#[derive(Debug)] enum DivisionResult { Ok(u32,u32), DivisionByZero, } fn divide(x:u32, y:u32) -> DivisionResult { if y == 0 { DivisionResult::DivisionByZero } else { DivisionResult::Ok(x / y, x % y) } } fn main() { if let DivisionResult::Ok(result,reminder) = divide(8,7) { println!("{} (remainder {})",result,reminder); }; }
Simplified matching with if let
Caution!
The single = is both an assignment and a pattern matching operator.
#[derive(Debug)] enum Direction { North, East, South, West, } use Direction::*; fn main() { let dir = North; if let North = dir { println!("North"); } }
if let with else
You can use else to match anything else.
#[derive(Debug)] enum Direction { North, East, South, West, } use Direction::*; fn main() { let dir = North; if let West = dir { println!("North"); } else { println!("Something else"); }; }
Enum variant goes on the left side
Caution!
You don't get a compile error, you get different behavior!
#[derive(Debug)] enum Direction { North, East, South, West, } use Direction::*; fn main() { let dir = North; // But it is important to have the enum // on the left hand side // if let West = dir { if let dir = West { println!("West"); } else { println!("Something else"); }; }
Single = for pattern matching
Remember to use the single = for pattern matching, not the double == for equality.
#[derive(Debug)] enum Direction { North, East, South, West, } use Direction::*; fn main() { let dir = North; // Don't do this. if let North == dir { println!("North"); } }
Best Practices
When to Use Enums:
- State representation: Modeling different states of a system
- Error handling: Representing success/failure with associated data
- Variant data: When you need a type that can be one of several things
- API design: Making invalid states unrepresentable
Design Guidelines:
- Use descriptive names: Make variants self-documenting
- Leverage associated data: Store relevant information with variants
- Prefer exhaustive matching: Avoid catch-all patterns when possible
- Use
if letfor single variant: When you only care about one case
In-Class Activity: "Traffic Light State Machine"
Activity Overview
Work in snall teams to create a simple traffic light system using enums and pattern matching.
Activity Instructions
You're given a TrafficLight enum.
Task:
- Create a function
next_lightthat takes aTrafficLightand returns the next state in the sequence: Red → Green(30) → Yellow(5) → Red(45) with the seconds remaining till the next light. - Create a function
get_light_colorthat takes a reference to aTrafficLight(&TrafficLight) and returns a string slice representation (&str) of the current light state - Create a function
get_time_remainingthat takes a reference to aTrafficLight(&TrafficLight) and returns the time remaining till the next light as au32 - Call next_light, and print the light color and the time remaining till the next light.
- Repeat this process 3 times.
#![allow(unused_variables)] #![allow(dead_code)] #[derive(Debug)] enum TrafficLight { Red(u32), // seconds remaining Yellow(u32), // seconds remaining Green(u32), // seconds remaining } // Your code here
Discussion Points
- How do we get the value out of the enum variants?
- How do we match on the enum variants?
A1 Midterm 1 Review
Table of Contents:
- Revision 1 Changes
- Reminders about the exam
- Development Tools
- Shell/Terminal Commands
- Git Commands
- Cargo Commands
- Quick Questions: Tools
- Rust Core Concepts
- Variables and Types
- String vs &str
- Quick Questions: Rust basics
- Functions
- Loops and Arrays
- Enums and Pattern Matching
- Midterm Strategy
Revision 1 Posted Oct 7.
Changes:
- Enabled Rust playground for all code blocks
- In Loops and Arrays, modified what is not important and important
- Deleted quesiton 15 about Some(x) and renumbered remaining questions
- Updated code slightly in new question number 16
Reminders about the exam
- Practice exam posted on Piazza
- Up to 5 pages of notes, double sided, any font size
- No electronic devices
- Bring a pencil!
- Spread out -- don't sit beside or in front or behind anyone
Development Tools
Shell/Terminal Commands
For the midterm, you should recognize and recall:
pwd- where am I?ls- what's here?ls -la- more info and hidden filesmkdir folder_name- make a foldercd folder_name- move into a foldercd ..- move up to a parent foldercd ~- return to the home directoryrm filename- delete a file
You DON'T need to: Memorize complex command flags or advanced shell scripting
Git Commands
For the midterm, you should recognize and recall:
git clone- get a repository, pasting in the HTTPS or SSH linkgit status- see what's changedgit log- see the commit historygit branch- list all branchesgit checkout branch_name- switch to a different branchgit checkout -b new_branch- create a branch callednew_branchand switch to itgit add .- stage all recent changesgit commit -m "my commit message"- create a commit with staged changesgit push- send what's on my machine to GitHubgit pull- get changes from GitHub to my machinegit merge branch_name- merge branchbranch_nameinto the current branch
You DON'T need to: revert, reset, resolving merge conflicts, pull requests
Cargo Commands
For the midterm, you should recognize and recall:
cargo new project_name- create projectcargo run- compile and runcargo run --release- compile and run with optimizations (slower to compile, faster to run)cargo build- just compile without runningcargo check- just check for errors without compilingcargo test- run tests
You DON'T need to know: Cargo.toml syntax, how Cargo.lock works, advanced cargo features
Quick Questions: Tools
Question 1
Which command shows your current location on your machine?
Question 2
What's the correct order for the basic Git workflow?
- A) add → commit → push
- B) commit → add → push
- C) push → add → commit
- D) add → push → commit
Question 3
Which cargo command compiles your code without running it?
Rust Core Concepts
Compilers vs Interpreters
Key Concepts
- Compiled languages (like Rust): Code is transformed into machine code before running
- Interpreted languages (like Python): Code is executed line-by-line at runtime
- The compiler checks your code for errors and translates it into machine code
- The machine code is directly executed by your computer - it isn't Rust anymore!
- A compiler error means your code failed to translate into machine code
- A runtime error means your machine code crashed while running
Rust prevents runtime errors by being strict at compile time!
Variables and Types
Key Concepts
- Defining variables:
let x = 5; - Mutability: Variables are immutable by default, use
let mutto allow them to change - Shadowing:
let x = x + 1;creates a newxvalue withoutmutand lets you change types - Basic types:
i32,f64,bool,char,&str,String - Rough variable sizes: Eg.
i32takes up 32-bits of space and its largest positive value is about half ofu32's largest value - Type annotations: Rust infers types (
let x = 5) or you can specify them (let x: i32 = 5) - Tuples: Creating (
let x = (2,"hi")), accessing (let y = x.0 + 1), destructuring (let (a,b) = x) - Arrays: Creating (
let x = [1,2,3]), accessing (let y = x[1]) - Accessing and indexing elements of arrays, tuples and enums.
What's Not Important
- Calculating exact variable sizes and max values
- 2's complement notation for negative integers
- Complex string manipulation details
String vs &str
Quick explanation
String= a string = owned text data (like a text file you own)&str= a "string slice = borrowed text data (like looking at someone else's text)- A string literal like
"hello"is a&str(you don't own it, it's baked into your program) - To convert from an &str to a String, use
"hello".to_string()orString::from("hello") - To convert from a String to an &str, use
&my_string(to create a "reference")
Don't stress! You can do most things with either one, and we won't make you do anything crazy with these.
Quick Questions: Rust basics
Question 4
What happens with this code?
#![allow(unused)] fn main() { let x = 5; x = 10; println!("{}", x); }
- A) Prints 5
- B) Prints 10
- C) Compiler error
- D) Runtime error
Question 5
What's the type of x after this code?
#![allow(unused)] fn main() { let x = 5; let x = x as f64; let x = x > 3.0; }
- A)
i32 - B)
f64 - C)
bool - D) Compiler error
Question 6
How do you access the second element of tuple t = (1, 2, 3)?
- A)
t[1] - B)
t.1 - C)
t.2 - D)
t(2)
Functions
Key Concepts
- Function signature:
fn name(param1: type1, param2: type2) -> return_type, returned value must matchreturn_type - Expressions and statements: Expressions reduce to values (no semicolon), statements take actions (end with semicolon)
- Returning with return or an expression: Ending a function with
return x;andxare equivalent - {} blocks are scopes and expressions: They reduce to the value of the last expression inside them
- Unit type: Functions without a return type return
() - Best practices: Keep functions small and single-purpose, name them with verbs
What's Not Important
- Ownership/borrowing mechanics (we'll cover this after the midterm)
- Advanced function patterns
Quick Questions: Functions
Question 7
What is the value of mystery(x)?
#![allow(unused)] fn main() { fn mystery(x: i32) -> i32 { x + 5; } let x = 1; mystery(x) }
- A) 6
- B)
i32 - C)
() - D) Compiler error
Question 8
Which is a correct function signature for a function that takes two integers and returns their sum?
Question 9
Which version will compile
#![allow(unused)] fn main() { // Version A fn func_a() { 42 } // Version B fn func_b() { 42; } }
- A) A
- B) B
- C) Both
- D) Neither
Question 10
What does this print?
#![allow(unused)] fn main() { let x = println!("hello"); println!("{:?}", x); }
- A) hello \n hello
- B) hello \n ()
- C) hello
- D) ()
- E) Compiler error
- F) Runtime error
Loops and Arrays
Key Concepts
- Ranges:
1..5vs1..=5 - Arrays: Creating (
[5,6]vs[5;6]), accessing (x[i]), 0-indexing - If/else: how to write
if / elseblocks with correct syntax - Loop types:
for,while,loop- how and when to use each breakandcontinue: For controlling loop flow- Basic enumerating
for (i, val) in x.iter().enumerate() - Compact notation (
let x = if y ...orlet y = loop {...) - Labeled loops, breaking out of an outer loop
What's Not Important
- Enumerating over a string array with
for (i, &item) in x.iter().enumerate()
Quick Questions: Loops & Arrays
Question 11
What's the difference between 1..5 and 1..=5?
Question 12
What does this print?
#![allow(unused)] fn main() { for i in 0..3 { if i == 1 { continue; } println!("{}", i); } }
Question 13
How do you get both index and value when looping over an array?
Enums and Pattern Matching
Key Concepts
- Enum definition: Creating custom types with variants
- Data in variants: Enums can hold data
matchexpressions: syntax by hand, needs to be exhaustive, how to use a catch-all (_)#[derive(Debug)]: For making enums printable- Data extraction: Getting values out of enum variants with
match,unwrap, orexpect
Quick Questions: Enums & Match
Question 14
What's wrong with this code?
#![allow(unused)] fn main() { enum Status { Loading, Complete, Error, } let stat = Status::Loading; match stat { Status::Loading => println!("Loading..."), Status::Complete => println!("Done!"), } }
Question 15
What does #[derive(Debug)] do?
Question 16
What does this return when called with divide_with_remainder(10, 2)?
How about with divide_with_remainder(10, 0)?
#![allow(unused)] fn main() { enum MyResult { Ok(u32,u32), // Store the result of the integer division and the remainder DivisionByZero, } fn divide_with_remainder(a: u32, b: u32) -> MyResult { if b == 0 { MyResult::DivisionByZero } else { MyResult::Ok(a / b, a % b) } } }
Midterm Strategy
- Focus on concepts: Understand the "why" behind the syntax and it will be easier to remember
- Practice with your hands: Literally and figuratively - practice solving problems, and practice on paper
- Take bigger problems step-by-step: Understand each line of code before reading the next. And make a plan before you start to hand-code
Good Luck!
Structs in Rust
About This Module
This module introduces Rust's struct (structure) types, which allow you to create custom data types by grouping related values together with named fields. Structs provide more semantic meaning than tuples by giving names to data fields and are fundamental for building complex data models.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 5: Structs Introduction
- Chapter 5.1: Defining and Instantiating Structs
- Chapter 5.2: An Example Program Using Structs
Pre-lecture Reflections
Before class, consider these questions:
- How do structs provide more semantic meaning than tuples?
- What are the advantages of named fields over positional access?
- How do tuple structs combine benefits of both tuples and structs?
- When would you choose structs over other data structures?
- How do structs help with type safety and preventing logical errors?
Learning Objectives
By the end of this module, you should be able to:
- Define and instantiate regular structs with named fields
- Create and use tuple structs for type safety
- Access and modify struct fields
- Use struct update syntax for efficient instantiation
- Understand when to use structs vs. tuples vs. other data types
- Apply structs in enum variants for complex data modeling
- Design data structures using struct composition
What Are Structs?
Definition:
A struct (structure) is a custom data type that lets you name and package together multiple related values. Unlike tuples, structs give meaningful names to each piece of data.
Key Benefits:
- Semantic meaning: Named fields make code self-documenting
- Type safety: Prevent mixing up different types of data
- Organization: Group related data logically
- Maintainability: Changes are easier when fields have names
Structs
Previously we saw tuples, e.g., (12, 1.7, true), where we can mix different types of data.
Structs compared to tuples:
- Similar: can hold items of different types
- Different: the items have names
#![allow(unused)] fn main() { // Definition: list items (called fields) // and their types struct Person { name: String, year_born: u16, time_100m: f64, likes_ice_cream: bool, } }
Struct Instantiation
- Replace types with values
struct Person { name: String, year_born: u16, time_100m: f64, likes_ice_cream: bool, } fn main() { let mut cartoon_character: Person = Person { name: String::from("Tasmanian Devil"), year_born: 1954, time_100m: 7.52, likes_ice_cream: true, }; }
Struct Field Access
- Use "." to access fields
struct Person { name: String, year_born: u16, time_100m: f64, likes_ice_cream: bool, } fn main() { let mut cartoon_character: Person = Person { name: String::from("Tasmanian Devil"), year_born: 1954, time_100m: 7.52, likes_ice_cream: true, }; // Accessing fields: use ".field_name" println!("{} was born in {}", cartoon_character.name, cartoon_character.year_born); cartoon_character.year_born = 2022; println!("{} was born in {}", cartoon_character.name, cartoon_character.year_born); }
Challenge: How would we update the last println! statement to print
Tasmanian Devil was born in 2022, can run a mile in 7.52 seconds and likes ice cream ?
Tuple Structs
Example: The tuple (f64,f64,f64) could represent:
- box size (e.g., height width depth)
- Euclidean coordinates of a point in 3D
We can use tuple structs to give a name to a tuple and make it more meaningful.
fn main() { struct BoxSize(f64,f64,f64); struct Point3D(f64,f64,f64); let mut my_box = BoxSize(3.2,6.0,2.0); let mut p : Point3D = Point3D(-1.3,2.1,0.0); }
Tuple Structs, cont.
- Impossible to accidentally confuse different types of triples.
- No runtime penalty! Verified at compilation.
fn main() { struct BoxSize(f64,f64,f64); struct Point3D(f64,f64,f64); let mut my_box = BoxSize(3.2,6.0,2.0); let mut p : Point3D = Point3D(-1.3,2.1,0.0); // won't work my_box = p; }
Tuple Structs, cont.
- Acessing via index
- Destructuring
fn main() { struct Point3D(f64,f64,f64); let mut p : Point3D = Point3D(-1.3,2.1,0.0); // Acessing via index println!("{} {} {}",p.0,p.1,p.2); p.0 = 17.2; // Destructuring let Point3D(first,second,third) = p; println!("{} {} {}", first, second, third); }
Named structs in enums
Structs with braces and exchangable with tuples in many places
enum LPSolution { None, Point{x:f64,y:f64} } fn main() { let example = LPSolution::Point{x:1.2, y:4.2}; if let LPSolution::Point{x:first,y:second} = example { println!("coordinates: {} {}", first, second); }; }
How is that different from enum variants with values?
enum LPSolution2 { None, Point(f64,f64) } fn main() { let example = LPSolution2::Point(1.2, 4.2); if let LPSolution2::Point(first,second) = example { println!("coordinates: {} {}", first, second); }; }
Recap and Next Steps
Recap
- Structs are a way to group related data together
- Tuple structs are a way to give a name to a tuple
- Named structs in enums are a way to group related data together
- Structs are critical to Rust's OO capabilities
Next Steps
- We will see how connect structs to methods (e.g. functions)
- Important step towards Object-Oriented style of programming in Rust
Method Syntax
About This Module
This module introduces method syntax in Rust, which brings aspects of object-oriented programming to the language by combining properties and methods in one object. You'll learn how methods are functions defined within the context of a struct and how to use impl blocks to define methods.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
Pre-lecture Reflections
Before class, consider these questions:
- How do methods differ from regular functions in Rust?
- What is the significance of the
selfparameter in method definitions? - When would you choose to use associated functions vs. methods?
- How do methods help with code organization and encapsulation?
- What are the benefits of the
implblock approach compared to other languages?
Learning Objectives
By the end of this module, you should be able to:
- Define methods within
implblocks for structs - Understand the role of
selfin method definitions - Create associated functions that don't take
self - Use methods to encapsulate behavior with data
- Apply method syntax for cleaner, more readable code
Method Syntax Overview
Brings aspects of object-oriented programming to Rust: combine properties and methods in one object.
Methods are functions that are defined within the context of a struct.
The first parameter is always self, which refers to the instance of the
struct the method is being called on.
Use and impl (implementation) block on the struct to define methods.
struct Point { // stores x and y coordinates x: f64, y: f64, } struct Rectangle { // store upper left and lower right points p1: Point, p2: Point, } impl Rectangle { // This is a method fn area(&self) -> f64 { // `self` gives access to the struct fields via the dot operator let Point { x: x1, y: y1 } = self.p1; let Point { x: x2, y: y2 } = self.p2; // `abs` is a `f64` method that returns the absolute value of the // caller ((x1 - x2) * (y1 - y2)).abs() } fn perimeter(&self) -> f64 { let Point { x: x1, y: y1 } = self.p1; let Point { x: x2, y: y2 } = self.p2; 2.0 * ((x1 - x2).abs() + (y1 - y2).abs()) } } fn main() { let rectangle = Rectangle { p1: Point{x:0.0, y:0.0}, p2: Point{x:3.0, y:4.0}, }; println!("Rectangle perimeter: {}", rectangle.perimeter()); println!("Rectangle area: {}", rectangle.area()); }
Associated Functions without self parameter
Useful as constructors.
You can have more than one impl block on the same struct.
struct Point { // stores x and y coordinates x: f64, y: f64, } struct Rectangle { // store upper left and lower right points p1: Point, p2: Point, } impl Rectangle { // This is a method fn area(&self) -> f64 { // `self` gives access to the struct fields via the dot operator let Point { x: x1, y: y1 } = self.p1; let Point { x: x2, y: y2 } = self.p2; // `abs` is a `f64` method that returns the absolute value of the // caller ((x1 - x2) * (y1 - y2)).abs() } fn perimeter(&self) -> f64 { let Point { x: x1, y: y1 } = self.p1; let Point { x: x2, y: y2 } = self.p2; 2.0 * ((x1 - x2).abs() + (y1 - y2).abs()) } } impl Rectangle { fn new(p1: Point, p2: Point) -> Rectangle { Rectangle { p1, p2 } // instantiate a Rectangle struct and return it } } fn main() { // instantiate a Rectangle struct and return it let rect = Rectangle::new(Point{x:0.0, y:0.0}, Point{x:3.0, y:4.0}); println!("Rectangle area: {}", rect.area()); }
Common Patterns
Builder Pattern with Structs:
struct Config { host: String, port: u16, debug: bool, timeout: u32, } impl Config { fn new() -> Self { Config { host: String::from("localhost"), port: 8080, debug: false, timeout: 30, } } fn with_host(mut self, host: &str) -> Self { self.host = String::from(host); self } fn with_debug(mut self, debug: bool) -> Self { self.debug = debug; self } } fn main() { // Usage let config = Config::new() .with_host("api.example.com") .with_debug(true); }
Methods Continued
About This Module
This module revisits and expands on method syntax in Rust, focusing on different types of self parameters and their implications for ownership and borrowing. You'll learn the differences between self, &self, and &mut self, and when to use each approach for method design.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 5.3: Method Syntax - Review
- Chapter 4.2: References and Borrowing - Focus on method calls
Pre-lecture Reflections
Before class, consider these questions:
- What are the implications of using
selfvs&selfvs&mut selfin method signatures? - How does method call syntax relate to function call syntax with explicit references?
- When would you design a method to take ownership of
self? - How do method calls interact with Rust's borrowing rules?
- What are the trade-offs between different
selfparameter types?
Learning Objectives
By the end of this module, you should be able to:
- Distinguish between
self,&self, and&mut selfparameter types - Understand when methods take ownership vs. borrow references
- Design method APIs that appropriately handle ownership and mutability
- Apply method call syntax with different reference types
- Recognize the implications of different
selfparameter choices
Method Review
We saw these in the previous lecture.
- We can add functions that are directly associated with structs and enums!
- Then we could call them:
road.display()orroad.update_speed(25)
- Then we could call them:
- How?
- Put them in the namespace of the type
- make
selfthe first argument
#[derive(Debug)] struct Road { intersection_1: u32, intersection_2: u32, max_speed: u32, } impl Road { // constructor fn new(i1:u32,i2:u32,speed:u32) -> Road { Road { intersection_1: i1, intersection_2: i2, max_speed: speed, } } // note &self: immutable reference fn display(&self) { println!("{:?}",*self); } } // You can invoke the display method on the road instance // or on a reference to the road instance. fn main() { let mut road = Road::new(1,2,35); road.display(); &road.display(); (&road).display(); }
In C++ the syntax is different. It would be something like:
road.display();(&road)->display();
Method with immutable self reference
Rember that self is a reference to the instance of the struct.
By default, self is an immutable reference, so we can't modify the struct.
The following will cause a compiler error.
#![allow(unused)] fn main() { struct Road { intersection_1: u32, intersection_2: u32, max_speed: u32, } // ERROR impl Road { fn update_speed(&self, new_speed:u32) { self.max_speed = new_speed; } } }
Method with mutable self reference
Let's change it to a mutable reference.
#[derive(Debug)] struct Road { intersection_1: u32, intersection_2: u32, max_speed: u32, } impl Road { // constructor fn new(i1:u32,i2:u32,speed:u32) -> Road { Road { intersection_1: i1, intersection_2: i2, max_speed: speed, } } // note &self: immutable reference fn display(&self) { println!("{:?}",*self); } fn update_speed(&mut self, new_speed:u32) { self.max_speed = new_speed; } } fn main() { let mut road = Road::new(1,2,35); road.display(); road.update_speed(45); road.display(); }
Methods that take ownership of self
There are some gotchas to be aware of.
Consider the following code:
#![allow(unused)] fn main() { #[derive(Debug)] struct Road { intersection_1: u32, intersection_2: u32, max_speed: u32, } impl Road { fn this_will_move(self) -> Road { // this will take ownership of the instance of Road self } fn this_will_not_move(&self) -> &Road { // this will _not_ take ownership of the instance of Road self } } }
We'll talk about ownership and borrowing in more detail later.
Methods that borrow self
Let's experiment a bit.
#![allow(unused_variables)] #[derive(Debug)] struct Road { intersection_1: u32, intersection_2: u32, max_speed: u32, } impl Road { // constructor fn new(i1:u32,i2:u32,speed:u32) -> Road { Road { intersection_1: i1, intersection_2: i2, max_speed: speed, } } // note &self: immutable reference fn display(&self) { println!("{:?}",*self); } fn update_speed(&mut self, new_speed:u32) { self.max_speed = new_speed; } fn this_will_move(self) -> Road { // this will take ownership of the instance of Road self } fn this_will_not_move(&self) -> &Road { self } } fn main() { let r = Road::new(1,2,35); // create a new instance of Road, r let r3 = r.this_will_not_move(); // create a new reference to r, r3 // run the code with the following line commented, then try uncommenting it //let r2 = r.this_will_move(); // this will take ownership of r r.display(); // r2.display(); r3.display(); }
Methods (summary)
- Make first parameter
self - Various options:
self: move will occur&self: self will be immutable reference&mut self: self will be mutable reference
In-Class Poll
A1 Piazza Poll:
Select ALL statements below that are true. Multiple answers may be correct.
- Structs can hold items of different types, similar to tuples
- Tuple structs provide type safety by preventing confusion between different tuple types
-
Methods with
&selfallow you to modify the struct's fields -
You can have multiple
implblocks for the same struct -
Associated functions without
selfare commonly used as constructors -
Enum variants can contain named struct-like data using curly braces
{} -
Methods are called using
::syntax, likerectangle::area()
In-Class Activity
Coding Exercise: Student Grade Tracker (15 minutes)
Objective: Practice defining structs and implementing methods with different types of self parameters.
Scenario: You're building a simple grade tracking system for a course. Create a Student struct and implement various methods to manage student information and grades.
You can work in teams of 2-3 students. Suggest cargo new grades-struct to create a new project and then work in VS Code.
Copy your answer into Gradescope.
Part 1: Define the Struct (3 minutes)
Create a Student struct with the following fields:
name: String (student's name)id: u32 (student ID number)grades: [f64; 5] (array of up to 5 grades)num_grades: usize (number of grades added)
Part 2: Implement Methods (10 minutes)
Implement the following methods in an impl block:
-
Constructor (associated function):
new(name: String, id: u32) -> Student- Creates a new student with grades initialized to
[0.0; 5]andnum_gradesset to 0
-
Immutable reference methods (
&self):display(&self)- debug prints the Student structaverage_grade(&self) -> f64- returns average grade- Optional:
get_letter_grade(&self) -> Option<char>- returns 'A' (≥90), 'B' (≥80), 'C' (≥70), 'D' (≥60), or 'F' (<60)
-
Mutable reference methods (
&mut self):add_grade(&mut self, grade: f64)- adds a grade to the student's record
Part 3: Test Your Implementation (2 minutes)
Write a main function that creates a new student.
We provide code to:
- Add several grades
- Displays the student info, average and letter grade
Expected Output Example:
Student { name: "Alice Smith", id: 12345, grades: [85.5, 92.0, 78.5, 88.0, 0.0], num_grades: 4 }
Average grade: 86
Letter grade: B
Starter Code:
#![allow(unused)] #[derive(Debug)] struct Student { // TODO: Add fields } impl Student { // TODO: Implement methods } fn main() { let mut student = ... // TODO: Create a new student // Add several grades student.add_grade(85.5); student.add_grade(92.0); student.add_grade(78.5); student.add_grade(88.0); // Display initial information student.display(); println!(); }
Ownership and Borrowing in Rust
Introduction
- Rust's most distinctive feature: ownership system
- Enables memory safety without garbage collection
- Compile-time guarantees with zero runtime cost
- Three key concepts: ownership, borrowing, and lifetimes
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 4: Understanding Ownership - All sections
Pre-lecture Reflections
Before class, consider these questions:
- What problems does Rust's ownership system solve compared to manual memory management?
- How does ownership differ from garbage collection in other languages?
- What is the difference between moving and borrowing a value?
- When would you use
Box<T>instead of storing data on the stack? - How do mutable and immutable references help prevent data races?
Memory Layout: Stack vs Heap
Stack:
- Fast, fixed-size allocation
- LIFO (Last In, First Out) structure
- Stores data with known, fixed size at compile time
- Examples: integers, booleans, fixed-size arrays
Heap:
- Slower, dynamic allocation
- For data with unknown or variable size
- Allocator finds space and returns a pointer
- Examples: String, Vec, Box
Stack Memory Example
fn main() { let x = 5; // stored on stack let y = true; // stored on stack let z = x; // copy of value on stack println!("{}, {}", x, z); // both still valid }
- Simple types implement
Copytrait - Assignment creates a copy, both variables remain valid
String and the Heap
Heap Memory: The String Type
Let's look more closely at the String type.
#![allow(unused)] fn main() { let s1 = String::from("hello"); }
Stringstores pointer, length, capacity on stack- Actual string data stored on heap
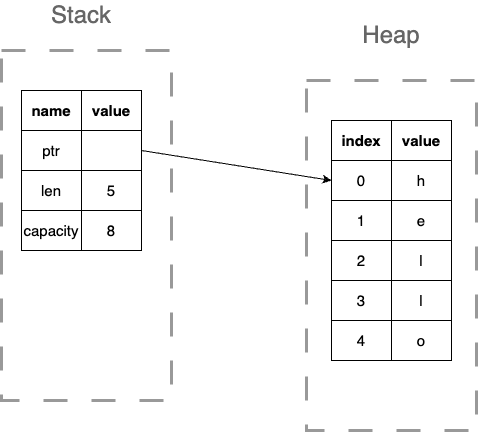
In fact we can inspect the memory layout of a String:
#![allow(unused)] fn main() { let mut s = String::from("hello"); println!("&s:{:p}", &s); println!("ptr: {:p}", s.as_ptr()); println!("len: {}", s.len()); println!("capacity: {}\n", s.capacity()); // Let's add some more text to the string s.push_str(", world!"); println!("&s:{:p}", &s); println!("ptr: {:p}", s.as_ptr()); println!("len: {}", s.len()); println!("capacity: {}", s.capacity()); }
Shallow Copy with Move
fn main() { let s1 = String::from("hello"); // s1 has three parts on stack: // - pointer to heap data // - length: 5 // - capacity: 5 let s2 = s1; // shallow copy of stack data println!("{}", s1); // ERROR! s1 is no longer valid println!("{}", s2); // OK }
Stringstores pointer, length, capacity on stack- Actual string data stored on heap
Shallow Copy:
- Copying the pointer, length, and capacity
- The actual string data is not copied
- The owner of the string data is transferred to the new structure
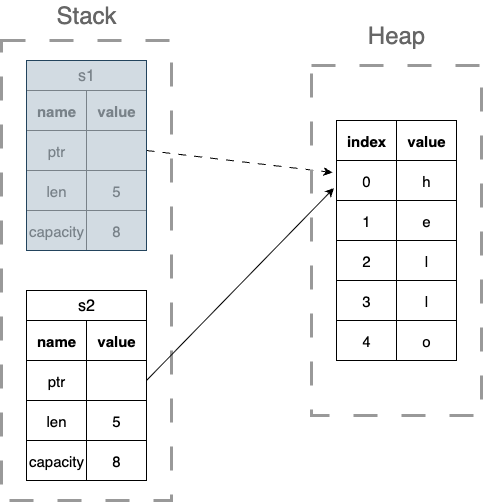
#![allow(unused)] fn main() { let s1 = String::from("hello"); println!("&s1:{:p}", &s1); println!("ptr: {:p}", s1.as_ptr()); println!("len: {}", s1.len()); println!("capacity: {}\n", s1.capacity()); let s2 = s1; println!("&s2:{:p}", &s2); println!("ptr: {:p}", s2.as_ptr()); println!("len: {}", s2.len()); println!("capacity: {}", s2.capacity()); }
The Ownership Rules
- Each value in Rust has an owner
- There can only be one owner at a time
- When the owner goes out of scope, the value is dropped
These rules prevent:
- Double free errors
- Use after free
- Data races
Ownership Transfer: Move Semantics
fn main() { let s1 = String::from("hello"); let s2 = s1; // ownership moves from s1 to s2 // s1 is now invalid - compile error if used println!("{}", s2); // OK // When s2 goes out of scope, memory is freed }
- Move prevents double-free
- Only one owner can free the memory
Clone: Deep Copy
fn main() { let s1 = String::from("hello"); let s2 = s1.clone(); // deep copy of heap data println!("s1 = {}, s2 = {}", s1, s2); // both valid }
clone()creates a full copy of heap data- Both variables are independent owners
- More expensive operation
Vec and the Heap
Vec: Dynamic Arrays on the Heap
What is Vec?
Vec<T>is Rust's growable, heap-allocated array type- Generic over type
T(e.g.,Vec<i32>,Vec<String>) - Contiguous memory allocation for cache efficiency
- Automatically manages capacity and growth
Three ways to create a Vec:
#![allow(unused)] fn main() { // 1. Empty vector with type annotation let v1: Vec<i32> = Vec::new(); // 2. Using vec! macro with initial values let v2 = vec![1, 2, 3, 4, 5]; // 3. With pre-allocated capacity let v3: Vec<i32> = Vec::with_capacity(10); }
Vec Memory Structure
#![allow(unused)] fn main() { let mut v = Vec::new(); v.push(1); v.push(2); v.push(3); // Vec structure (on stack): // - pointer to heap buffer // - length: 3 (number of elements) // - capacity: (at least 3, often more) println!("&v:{:p}", &v); println!("ptr: {:p}", v.as_ptr()); println!("Length: {}", v.len()); println!("Capacity: {}", v.capacity()); }
- Pointer: points to heap-allocated buffer
- Length: number of initialized elements
- Capacity: total space available before reallocation
Vec Growth and Reallocation
fn main() { let mut v = Vec::new(); println!("Initial capacity: {}", v.capacity()); // 0 v.push(1); println!("After 1 push: {}", v.capacity()); // typically 4 v.push(2); v.push(3); v.push(4); v.push(5); // triggers reallocation println!("After 5 pushes: {}", v.capacity()); // typically 8 }
- Capacity doubles when full (amortized O(1) push)
- Reallocation: new buffer allocated, old data copied
- Pre-allocate with
with_capacity()to avoid reallocations
Accessing Vec Elements
fn main() { let v = vec![10, 20, 30, 40, 50]; // Indexing - panics if out of bounds let third = v[2]; println!("Third element: {}", third); // Using get() - returns Option<T> // Safely handles out of bounds indices match v.get(2) { Some(value) => println!("Third element: {}", value), None => println!("No element at index 2"), } }
Option<T>
Option<T> is an enum that can be either Some(T) or None.
Defined in the standard library as:
#![allow(unused)] fn main() { enum Option<T> { Some(T), None, } }
Let's you handle the case where there is no return value.
fn main() { let v = vec![1, 2, 3, 4, 5]; match v.get(0) { Some(value) => println!("Element: {}", value), None => println!("No element at index"), } }
Modifying Vec Elements
fn main() { let mut v = vec![1, 2, 3, 4, 5]; // Direct indexing for modification v[0] = 10; // Adding elements v.push(6); // add to end // Removing elements let last = v.pop(); // remove from end, returns Option<T> // Insert/remove at position v.insert(2, 99); // insert 99 at index 2 v.remove(1); // remove element at index 1 println!("{:?}", v); }
Vec Ownership
fn main() { let v1 = vec![1, 2, 3, 4, 5]; let v2 = v1; // ownership moves // println!("{:?}", v1); // ERROR! println!("{:?}", v2); // OK let v3 = v2.clone(); // deep copy println!("{:?}, {:?}", v2, v3); // both OK }
- Vec follows same ownership rules as String
- Move transfers ownership of heap allocation
Functions and Ownership
Functions and Ownership
fn takes_ownership(s: String) { println!("{}", s); } // s is dropped here fn main() { let s = String::from("hello"); takes_ownership(s); // println!("{}", s); // ERROR! s was moved }
- Passing to function transfers ownership
- Original variable becomes invalid
Returning Ownership
fn gives_ownership(s: String) -> String { let new_s = s + " world"; new_s // ownership moves to caller } fn main() { let s1 = String::from("hello"); let s2 = gives_ownership(s1); println!("{}", s2); // OK }
- Return value transfers ownership out of function
- Caller becomes new owner
References: Borrowing Without Ownership
fn main() { let s1 = String::from("hello"); let len = calculate_length(&s1); // borrow with & println!("'{}' has length {}", s1, len); // s1 still valid! } fn calculate_length(s: &String) -> usize { s.len() } // s goes out of scope, but doesn't own data
&creates a reference (borrow)- Original owner retains ownership
- Reference allows reading data
Immutable References
fn main() { let s = String::from("hello"); let r1 = &s; // immutable reference let r2 = &s; // another immutable reference let r3 = &s; // yet another println!("{}, {}, {}", r1, r2, r3); // all valid // Let's take a look at the memory layout println!("&s: {:p}, s.as_ptr(): {:p}", &s, s.as_ptr()); println!("&r1: {:p}, r1.as_ptr(): {:p}", &r1, r1.as_ptr()); println!("&r2: {:p}, r2.as_ptr(): {:p}", &r2, r2.as_ptr()); println!("&r3: {:p}, r3.as_ptr(): {:p}", &r3, r3.as_ptr()); }
- Multiple immutable references allowed simultaneously
- Cannot modify through immutable reference
// ERROR fn main() { let s = String::from("hello"); change(&s); println!("{}", s); } fn change(s: &String) { s.push_str(", world"); }
Mutable References
fn main() { let mut s = String::from("hello"); change(&mut s); // mutable reference with &mut println!("{}", s); // prints "hello, world" } fn change(s: &mut String) { s.push_str(", world"); }
&mutcreates mutable reference- Allows modification of borrowed data
Mutable Reference Restrictions
fn main() { let mut s = String::from("hello"); let r1 = &mut s; let r2 = &mut s; // ERROR! Only one mutable reference println!("{}", r1); }
- Only ONE mutable reference at a time
- Prevents data races at compile time
- No simultaneous readers when there's a writer
Mixing References: Not Allowed
fn main() { let mut s = String::from("hello"); let r1 = &s; // immutable let r2 = &s; // immutable let r3 = &mut s; // ERROR! Can't have mutable with immutable println!("{}, {}", r1, r2); }
- Cannot have mutable reference while immutable references exist
- Immutable references expect data won't change
Reference Scopes and Non-Lexical Lifetimes
fn main() { let mut s = String::from("hello"); let r1 = &s; let r2 = &s; println!("{}, {}", r1, r2); // r1 and r2 no longer used after this point let r3 = &mut s; // OK! Previous references out of scope println!("{}", r3); }
- Reference scope: from introduction to last use, rather than lexical scope (till end of block)
- Non-lexical lifetimes allow more flexible borrowing
Vec with References
fn main() { let mut v = vec![1, 2, 3, 4, 5]; let first = &v[0]; // immutable borrow // v.push(6); // ERROR! Can't mutate while borrowed println!("First element: {}", first); v.push(6); // OK now, first is out of scope }
- Borrowing elements prevents mutation of Vec
- Protects against invalidation (reallocation)
Function Calls: Move vs Reference vs Mutable Reference
fn process_string(s: String) { } // takes ownership (move) fn read_string(s: &String) { } // immutable borrow fn modify_string(s: &mut String) { } // mutable borrow fn main() { let mut s = String::from("hello"); read_string(&s); // borrow modify_string(&mut s); // mutable borrow read_string(&s); // borrow again process_string(s); // move // s is now invalid }
Method Calls with Different Receivers
#![allow(unused)] fn main() { impl String { // Takes ownership: self fn into_bytes(self) -> Vec<u8> { /* ... */ } // Immutable borrow: &self fn len(&self) -> usize { /* ... */ } // Mutable borrow: &mut self fn push_str(&mut self, s: &str) { /* ... */ } } }
self: method takes ownership (consuming)&self: method borrows immutably&mut self: method borrows mutably
Method Call Examples
- It can be difficult to understand which ownership rules are being applied to a method call.
fn main() { let mut s = String::from("hello"); let len = s.len(); // &self - immutable borrow println!("{}, length: {}", s, len); s.push_str(" world 🌎"); // &mut self - mutable borrow let len = s.len(); // &self - immutable borrow println!("{}, length: {}", s, len); let bytes = s.into_bytes(); // self - takes ownership // s is now invalid println!("{:?}", bytes); let t = String::from_utf8(bytes).unwrap(); println!("{}", t); }
Vec Method Patterns
fn main() { let mut v = vec![1, 2, 3]; v.push(4); // &mut self let last = v.pop(); // &mut self, returns Option<T> let len = v.len(); // &self // Immutable iteration // What happens if you take away the &? for item in &v { // iterate with &Vec println!("{}", item); } // Mutable iteration for item in &mut v { // iterate with &mut Vec *item *= 2; println!("{}", item); } println!("{:?}", v); // Taking ownership for item in v { println!("{}", item); } //println!("{:?}", v); // ERROR! v is now invalid }
Note: It is instructive to create a Rust project and put this mode in
main.rsthen look at it in VSCode with the Rust Analyzer extension. Note the datatype decorations that VSCode places next to the variables.
Note #2: The
println!macro is pretty flexible in the types of arguments it can take. In the example above, we are passing it a&i32, a&mut i32, and ai32.
Key Takeaways
- Stack: fixed-size, fast; Heap: dynamic, flexible
- Ownership ensures memory safety without garbage collection
- Move semantics prevent double-free
- Borrowing allows temporary access without ownership transfer
- One mutable reference XOR many immutable references
- References must be valid (no dangling pointers)
- Compiler enforces these rules at compile time
Best Practices
- Prefer borrowing over ownership transfer when possible
- Use immutable references by default
- Keep mutable reference scope minimal
- Let the compiler guide you with error messages
- Clone only when necessary (performance cost)
- Understand whether functions need ownership or just access
In-Class Exercise (10 minutes)
Challenge: Fix the Broken Code
The following code has several ownership and borrowing errors. Your task is to fix them so the code compiles and runs correctly.
I'll call on volunteers to present their solutions.
fn main() { let mut numbers = vec![1, 2, 3, 4, 5]; // Task 1: Calculate sum without taking ownership let total = calculate_sum(numbers); // Task 2: Double each number in the vector double_values(numbers); // Task 3: Print both the original and doubled values println!("Original sum: {}", total); println!("Doubled values: {:?}", numbers); // Task 4: Add new numbers to the vector add_numbers(numbers, vec![6, 7, 8]); println!("After adding: {:?}", numbers); } fn calculate_sum(v: Vec<i32>) -> i32 { let mut sum = 0; for num in v { sum += num; } sum } fn double_values(v: Vec<i32>) { for num in v { num *= 2; } } fn add_numbers(v: Vec<i32>, new_nums: Vec<i32>) { for num in new_nums { v.push(num); } }
Hints:
- Think about which functions need ownership vs borrowing
- Consider when you need
&vs&mut - Remember: you can't modify through an immutable reference
- The original vector should still be usable in
mainafter function calls
Let's Review
Review solutions.
Slices in Rust
About This Module
This module introduces slices, a powerful feature in Rust that provides references to contiguous sub-sequences of collections. We'll explore how slices work with arrays and vectors, their memory representation, and how they interact with Rust's borrowing rules.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
You might want to go back and review:
Pre-lecture Reflections
Before class, consider these questions:
- How do slices provide safe access to sub-sequences without copying data?
- What are the advantages of slices over passing entire arrays or vectors?
- How do borrowing rules apply to slices and prevent data races?
- When would you use slices instead of iterators for processing sub-sequences?
- What are the memory efficiency benefits of slices compared to copying data?
Learning Objectives
By the end of this module, you should be able to:
- Create and use immutable and mutable slices from arrays and vectors
- Understand slice syntax and indexing operations
- Apply borrowing rules correctly when working with slices
- Analyze the memory representation of slices
- Use slices for efficient sub-sequence processing without data copying
- Design functions that work with slice parameters for flexibility
Slices (§4.3)
Slice = reference to a contiguous sub-sequence of elements in a collection
Slices of an array:
- array of type
[T, _], e.g. datatype and length - slice of type
&[T](immutable) or&mut [T](mutable)
fn main() { let arr: [i32; 5] = [0,1,2,3,4]; println!("arr: {:?}", arr); // immutable slice of an array let slice: &[i32] = &arr[1..3]; println!("slice: {:?}",slice); println!("slice[0]: {}", slice[0]); }
The slice slice is a reference to the array arr from index 1 to 3 and hence is borrowed from arr.
Immutable slices
Note:
- The slice is a reference to the array, which by default is immutable.
- Even if the source array is mutable, the slice is immutable.
fn main() { let mut arr: [i32; 5] = [0,1,2,3,4]; println!("arr: {:?}", arr); // immutable slice of an array let slice: &[i32] = &arr[1..3]; println!("slice: {:?}",slice); println!("slice[0]: {}", slice[0]); slice[0] = 100; // ERROR! Cannot modify an immutable slice println!("slice: {:?}", slice); println!("slice[0]: {}", slice[0]); }
Mutable slices
We can create a mutable slice from a mutable array which borrows from arr mutably.
fn main(){ // mutable slice of an array let mut arr = [0,1,2,3,4]; println!("arr: {:?}", arr); let mut slice = &mut arr[2..4]; println!("slice: {:?}",slice); // ERROR: Cannot modify the source array after a borrow //arr[0] = 10; //println!("arr: {:?}", arr); println!("\nLet's modify the slice[0]"); slice[0] = slice[0] * slice[0]; println!("slice[0]: {}", slice[0]); println!("slice: {:?}", slice); println!("arr: {:?}", arr); }
What about this?
What's happening here?!?!?
Why are we able to modify the array after the slice is created?
fn main() { let mut arr: [i32; 5] = [0,1,2,3,4]; println!("arr: {:?}", arr); // immutable slice of an array let slice: &[i32] = &arr[1..3]; println!("slice: {:?}",slice); println!("slice[0]: {}", slice[0]); arr[0] = 10; // OK! We can modify the array println!("arr: {:?}", arr); // What happens if you uncomment this line? //println!("slice: {:?}", slice); }
Answer:
Slices with Vectors
Work for vectors too!
fn main() { let mut v = vec![0,1,2,3,4]; { let slice = &v[1..3]; println!("{:?}",slice); } { let mut slice = &mut v[1..3]; // iterating over slices works as well for x in slice { *x *= 1000; } }; println!("{:?}",v); }
Slices are references: all borrowing rules still apply!
- At most one mutable reference at a time
- No immutable references allowed with a mutable reference
- Many immutable references allowed simultaneously
#![allow(unused)] fn main() { // this won't work! let mut v = vec![1,2,3,4,5,6,7]; { let ref_1 = &mut v[2..5]; let ref_2 = &v[1..3]; ref_1[0] = 7; println!("{}",ref_2[1]); } }
#![allow(unused)] fn main() { // and this reordering will let mut v = vec![1,2,3,4,5,6,7]; { let ref_1 = &mut v[2..5]; ref_1[0] = 7; // ref_1 can be dropped let ref_2 = &v[1..3]; println!("{}",ref_2[1]); } }
Memory representation of slices
- Pointer
- Length
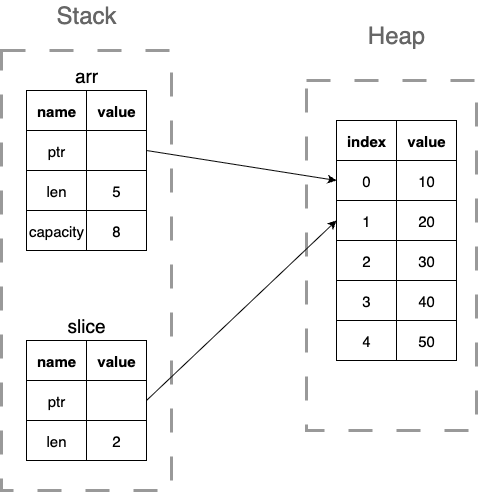
Let's return to &str?
&str is slice
-
&strcan be a slice of a string literal or a slice of aString -
&stritself (the reference) is stored on the stack, -
but the string data it points to can be in different locations depending on the context.
Let's break this down:
The &str Data (Various Locations)
The actual string data that &str points to can be in:
- Binary's read-only data segment (most common for string literals):
#![allow(unused)] fn main() { let s: &str = "hello"; // "hello" is in read-only memory println!("&s:{:p}", &s); println!("ptr: {:p}", s.as_ptr()); println!("len: {}", s.len()); // println!("capacity: {}\n", s.capacity()); // ERROR! Not applicable }
- Heap (when it's a slice of a
String):
#![allow(unused)] fn main() { let string = String::from("hello"); let s: &str = &string; // points to heap-allocated data println!("&s:{:p}", &s); println!("ptr: {:p}", s.as_ptr()); println!("len: {}", s.len()); }
True/False Statements on Rust Slices
A slice of type `&[i32]` is always immutable, even if it's created from a mutable array.
TRUE - "The slice is a reference to the array, which by default is immutable. Even if the source array is mutable, the slice is immutable." To get a mutable slice, you need to explicitly use `&mut [T]` syntax.
Slices in Rust consist of two components in memory: a pointer to the data and a length.
TRUE
You can have both an immutable slice and a mutable slice of the same vector active at the same time.
FALSE - Slices are references: all borrowing rules still apply!
The `&str` type is a slice, and the actual string data it points to is always stored in the binary's read-only data segment.
FALSE. While `&str` is indeed a slice, the string data it points to can be in different locations depending on the context, including the binary's read-only data segment (for string literals) or the heap (when it's a slice of a `String`).
Slices work with both arrays and vectors in Rust.
TRUE
Enter your answers into piazza poll.
Summary
- Slices are references to contiguous sub-sequences of elements in a collection
- Slices are immutable by default
- We can create mutable slices from mutable arrays
- Slices are references: all borrowing rules still apply!
&stris a slice of a string literal or a slice of aString&stritself (the reference) is stored on the stack, but the string data it points to can be in different locations depending on the context.
Modules and Organization
About This Module
This module introduces Rust's module system for organizing code into logical namespaces. You'll learn how to create modules, control visibility with public/private access, navigate module hierarchies, and organize code across multiple files.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 7: Managing Growing Projects with Packages, Crates, and Modules - Complete chapter
- Chapter 7.2: Defining Modules to Control Scope and Privacy
- Chapter 7.4: Bringing Paths into Scope with the use Keyword
Pre-lecture Reflections
Before class, consider these questions:
- Why is code organization important in larger software projects?
- What are the benefits of controlling which parts of your code are public vs. private?
- How do namespaces prevent naming conflicts in large codebases?
- When would you organize code into separate files vs. keeping it in one file?
- How do module systems help with code maintainability and collaboration?
Learning Objectives
By the end of this module, you should be able to:
- Create and organize code using Rust's module system
- Control access to code using
puband private visibility - Navigate module hierarchies using paths and
usestatements - Organize modules across multiple files and directories
- Design clean module interfaces for code reusability
- Apply module patterns to structure larger programs
Introduction to Modules
Up to now: our functions and data types (mostly) in the same namespace:
- exception: functions in structs and enums
Question: What is a namespace?
One can create a namespace, using mod
mod things_to_say { fn say_hi() { say("Hi"); } fn say_bye() { say("Bye"); } fn say(what: &str) { println!("{}!",what); } } fn main() {}
Intro, continued...
You have to use the module name to refer to a function.
That's necessary, but not sufficient!
mod things_to_say { fn say_hi() { say("Hi"); } fn say_bye() { say("Bye"); } fn say(what: &str) { println!("{}!",what); } } fn main() { // ERROR: function `say_hi` is private things_to_say::say_hi(); }
Module Basics
-
By default, all definitions in the namespace are private.
-
Advantage: Can hide all internally used code and control external interface
-
Use
pubto make functions or types public
mod things_to_say { pub fn say_hi() { say("Hi"); } pub fn say_bye() { say("Bye"); } fn say(what: &str) { println!("{}!",what); } } fn main() { things_to_say::say_hi(); things_to_say::say_bye(); // ERROR: function `say` is private //things_to_say::say("Say what??"); }
Why modules?
-
limit number of additional identifiers in the main namespace
-
organize your codebase into meaningful parts
-
hide auxiliary internal code
-
By default, all definitions in the namespace are private.
-
Advantage: one can hide all internally used code and publish an external interface
-
Ideally you semantically version your external interface. See https://semver.org
-
Use
pubto make functions or types public
Nesting possible
mod level_1 { mod level_2_1 { mod level_3 { pub fn where_am_i() {println!("3");} } pub fn where_am_i() {println!("2_1");} } mod level_2_2 { pub fn where_am_i() {println!("2_2");} } pub fn where_am_i() {println!("1");} } fn main() { level_1::level_2_1::level_3::where_am_i(); }
Nesting, continued...
But all parent modules have to be public as well.
mod level_1 { pub mod level_2_1 { pub mod level_3 { pub fn where_am_i() {println!("3");} } pub fn where_am_i() {println!("2_1");} } pub mod level_2_2 { pub fn where_am_i() {println!("2_2");} } pub fn where_am_i() {println!("1");} } fn main() { level_1::level_2_2::where_am_i(); }
Module Hierarchy
level_1
├── level_2_1
│ └── level_3
│ └── where_am_i
│ └── where_am_i
├── level_2_2
│ └── where_am_i
└── where_am_i
Paths to modules
pub mod level_1 { pub mod level_2_1 { pub mod level_3 { pub fn where_am_i() {println!("3");} pub fn call_someone_else() { where_am_i(); } } pub fn where_am_i() {println!("2_1");} } pub mod level_2_2 { pub fn where_am_i() {println!("2_2");} } pub fn where_am_i() {println!("1");} } fn where_am_i() {println!("main namespace");} fn main() { level_1::level_2_1::level_3::call_someone_else(); }
Question: What will be printed?
Paths to modules
Global paths: start from crate
mod level_1 { pub mod level_2_1 { pub mod level_3 { pub fn where_am_i() {println!("3");} pub fn call_someone_else() { crate::where_am_i(); crate::level_1::level_2_2:: where_am_i(); where_am_i(); } } pub fn where_am_i() {println!("2_1");} } pub mod level_2_2 { pub fn where_am_i() {println!("2_2");} } pub fn where_am_i() {println!("1");} } fn where_am_i() {println!("main namespace");} fn main() { level_1::level_2_1::level_3::call_someone_else(); }
Question: What will be printed?
Paths to modules
Local paths:
- going one or many levels up via
super
mod level_1 { pub mod level_2_1 { pub mod level_3 { pub fn where_am_i() {println!("3");} pub fn call_someone_else() { super::where_am_i(); super::super::where_am_i(); super::super:: level_2_2::where_am_i(); } } pub fn where_am_i() {println!("2_1");} } pub mod level_2_2 { pub fn where_am_i() {println!("2_2");} } pub fn where_am_i() {println!("1");} } fn where_am_i() {println!("main namespace");} fn main() { level_1::level_2_1::level_3::call_someone_else(); }
Question: What will be printed?
use to import things into the current scope
mod level_1 { pub mod level_2_1 { pub mod level_3 { pub fn where_am_i() {println!("3");} pub fn call_someone_else() { super::where_am_i(); } pub fn i_am_here() {println!("I am here");} } pub fn where_am_i() {println!("2_1");} } pub mod level_2_2 { pub fn where_am_i() {println!("2_2");} } pub fn where_am_i() {println!("1");} } fn where_am_i() {println!("main namespace");} fn main() { // Bring a submodule to current scope: use level_1::level_2_2; level_2_2::where_am_i(); // Bring a specific function/type to current scope: // (Don't do that, it can be confusing). use level_1::level_2_1::where_am_i; where_am_i(); // Bring multiple items to current scope: use level_1::level_2_1::level_3::{call_someone_else, i_am_here}; call_someone_else(); i_am_here(); // ERROR: Name clash! Won't work! //use level_1::where_am_i; //where_am_i(); }
Structs within modules
- You can put structs and methods in modules
- Fields are private by default
- Use
pubto make fields public
pub mod test { #[derive(Debug)] pub struct Point { x: i32, pub y: i32, } impl Point { pub fn create(x:i32,y:i32) -> Point { Point{x,y} } } } use test::Point; fn main() { let mut p = Point::create(2,3); println!("{:?}",p); p.x = 3; // Error: try commenting this out p.y = 4; // Why does this work? println!("{:?}",p); }
Structs within modules
Make fields and functions public to be accessible
mod test { #[derive(Debug)] pub struct Point { pub x: i32, y: i32, // still private } impl Point { pub fn create(x:i32,y:i32) -> Point { Point{x,y} } // public function can access private data pub fn update_y(&mut self, y:i32) { self.y = y; } } } use test::Point; fn main() { let mut p = Point::create(2,3); println!("{:?}",p); p.x = 3; println!("{:?}",p); p.update_y(2022); // only way to update y println!("{:?}",p); // The create function seemed trivial in the past but the following won't work: //let mut q = Point{x: 4, y: 5}; }
True/False Statements on Rust Modules
In Rust, all definitions within a module are private by default, and you must use the `pub` keyword to make them accessible outside the module.
TRUE
When accessing a nested module function, only the innermost module and the function need to be declared as `pub` - parent modules can remain private.
FALSE - parent modules must also be public
The `super` keyword is used to navigate up one or more levels in the module hierarchy, while `crate` refers to the root of the current crate for absolute paths.
TRUE - `super` navigates up, `crate` provides global paths
Fields in a struct are public by default, so you need to use the `priv` keyword to make them private within a module.
FALSE - fields are private by default, use `pub` to make them public
Using the `use` statement to bring a submodule into scope is recommended, but bringing individual functions directly into the current scope can be confusing and is discouraged in the lecture.
TRUE - Don't do that, it can be confusing.
Enter your answers into piazza poll.
Recap
- You can put structs and methods in modules
- Fields are private by default
- Use
pubto make fields public - Use
useto import things into the current scope - Use
modto create modules - Use
crateandsuperto navigate the module hierarchy
Rust Crates and External Dependencies
About This Module
This module introduces Rust's package management system through crates, which are reusable libraries and programs. Students will learn how to find, add, and use external crates in their projects, with hands-on experience using popular crates like rand, csv, and serde. The module covers the distinction between binary and library crates, how to manage dependencies in Cargo.toml, and best practices for working with external code.
Prework
Before this lecture, please read:
- The Rust Book Chapter 7: "Managing Growing Projects with Packages, Crates, and Modules"
- The Rust Book Chapter 14: "More about Cargo and Crates.io"
Pre-lecture Reflections
- What is the difference between a package, crate, and module in Rust?
- How does Cargo manage dependencies and versions?
- Why might you choose to use an external crate versus implementing functionality yourself?
Learning Objectives
By the end of this lecture, you should be able to:
- Distinguish between binary and library crates
- Add external dependencies to your Rust project using
Cargo.toml - Use popular crates like
rand,csv, andserdein your code - Understand semantic versioning and dependency management
- Evaluate external crates for trustworthiness and stability
What are crates?
Crates provided by a project:
- Binary Crate: Programs you compile to an executable and run.
- Each must have a
main()function that is the program entry point - So far we have seen single binaries
- Each must have a
- Library Crate: Define functionality than can be shared with multiple projects.
- Do not have a
main()function - A single library crate: can be used by other projects
- Do not have a
Shared crates
Where to find crates:
Documentation:
Crate rand: random numbers
Tell Rust you want to use it:
cargo add randfor the latest versioncargo add rand --version="0.8.5"for a specific versioncargo remove randto remove it
This adds to Cargo.toml:
[dependencies]
rand = "0.8.5"
Note: Show demo in VS Code.
Question: Why put the version number in Cargo.toml?
To generate a random integer from 1 through 100:
extern crate rand; // only needed in mdbook use rand::Rng; fn main() { let mut rng = rand::rng(); let secret_number = rng.random_range(1..=100); println!("The secret number is: {secret_number}"); }
Useful Crates
csv: reading and writing CSV filesserde: serializing and deserializing dataserde_json: serializing and deserializing JSON data
See: crates.io/crates/csv See: crates.io/crates/serde See: crates.io/crates/serde_json
Rust Project Organization and Multi-Binary Projects
About This Module
This module covers advanced Rust project organization, focusing on how to structure projects with multiple binaries and libraries. Students will learn about Rust's package system, understand the relationship between packages, crates, and modules, and gain hands-on experience organizing complex projects. The module also discusses best practices for managing external dependencies and the trade-offs involved in using third-party crates.
Prework
Before this lecture, please read:
- The Rust Book Chapter 7: "Managing Growing Projects with Packages, Crates, and Modules"
- The Rust Book Chapter 7.1: "Packages and Crates"
Pre-lecture Reflections
- What are the conventional file locations for binary and library crates in a Rust project?
- How does Rust's module system help organize large projects?
- What are the security and maintenance implications of depending on external crates?
Learning Objectives
By the end of this lecture, you should be able to:
- Organize Rust projects with multiple binaries and libraries
- Understand the Rust module system hierarchy (packages → crates → modules)
- Configure
Cargo.tomlfor complex project structures - Evaluate external dependencies for trustworthiness and stability
- Apply best practices for project organization and dependency management
Using Multiple Libraries or Binaries in your Project
-
So far, we went from a single source file, to multiple source files organized as Modules.
-
But we built our projects into single binaries with
cargo buildorcargo run. -
We can also build multiple binaries.
When we create a new program with cargo new my_program, it creates a folder
.
├── Cargo.toml
└── src
└── main.rs
And Cargo.toml has:
[package]
name = "my_program"
version = "0.1.0"
edition = "2024"
[dependencies]
Our program is considered a Rust package with the source in src/main.rs
that compiles (cargo build) into a single binary at target/debug/my_program.
The Rust Module System
- Packages: Cargo's way of organizing, building, testing, and sharing crates
- It's a bundle of one or more crates.
- Crates: A tree of modules that produces a library or executable
- Modules and
use: Let you control the organization, scope, and privacy of paths - Paths: A way of naming an item, such as a struct, function, or module, e.g.
my_library::library1::my_function
A package can contain as many binary crates as you want, but only one library crate.
By default src/main.rs is the crate root of a binary crate with the same name as the package (e.g. my_program).
Also by default, src/lib.rs would contain a library crate with the same name as the package and src/lib.rs is its crate root.
How to add multiple binaries to your project
[[bin]]
name = "some_name"
path = "some_directory/some_file.rs"
The file some_file.rs must contain a fn main()
How to add a library to your project
[lib]
name = "some_name"
path = "src/lib/lib.rs"
The file lib.rs does not need to contain a fn main()
You can have as many binaries are you want in a project but only one library!
Example: simple_package
Create a new project with cargo new simple_package.
Copy the code below so your has the same structure and contents.
- Try
cargo run. - Since there are two binaries, you can try
cargo run --bin first_binorcargo run --bin second_bin.
.
├── Cargo.lock
├── Cargo.toml
└── src
├── bin
│ └── other.rs
├── lib
│ ├── bar.rs
│ ├── foo.rs
│ └── lib.rs
└── main.rs
Cargo.toml:
[package]
name = "simple_library2"
version = "0.1.0"
edition = "2021"
# the double brackets indicate this is part of an array of bins
[[bin]]
name = "first_bin"
path = "src/main.rs"
[[bin]]
name = "second_bin"
path = "src/bin/other.rs"
# single bracket means we can have only one lib
[lib]
name = "librs"
path = "src/lib/lib.rs"
[dependencies]
src/bin/other.rs:
use librs;
fn main() {
println!("This is other.rs using a library");
librs::bar::say_something();
}src/lib/bar.rs:
use crate::foo;
pub fn say_something() {
println!("Bar");
foo::say_something();
}src/lib/foo.rs:
pub fn say_something() {
println!("Foo");
}src/lib/lib.rs:
/*
* This will make the compiler look for either:
* 1. src/lib/bar.rs or
* 2. src/lib/bar/mod.rs
*/
pub mod bar;
/*
* This will make the compiler look for either:
* 1. src/lib/foo.rs or
* 2. src/lib/foo/mod.rs
*/
pub mod foo;src/main.rs:
use librs;
fn main() {
println!("This is main.rs using a library");
librs::bar::say_something();
}Relying on external projects
Things to consider about external libraries:
- trustworthy?
- stable?
- long–term survival?
- do you really need it?
Many things best left to professionals:
Never implement your own cryptography!
Implementing your own things can be a great educational experience!
Extreme example
Yanking a published module version: article about left-pad
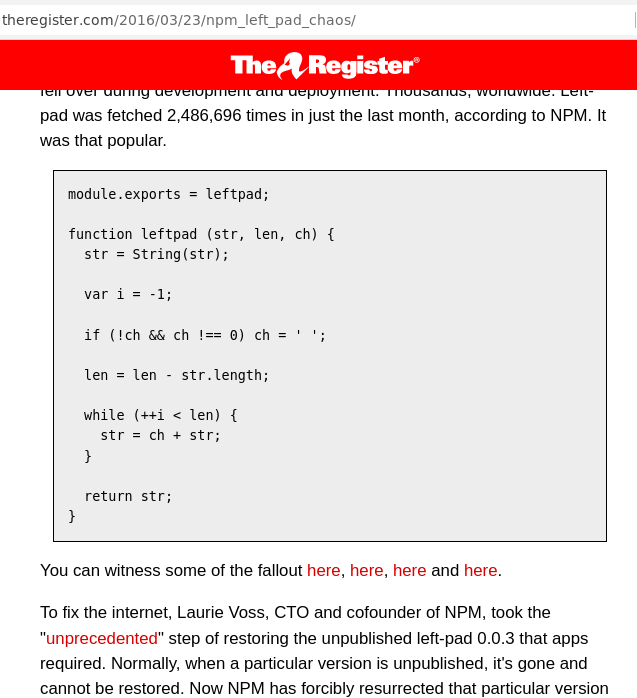
Rust and cargo: can't delete libraries that were published.
Testing in Rust: Ensuring Code Quality
About This Module
This short module introduces testing in Rust, covering how to write effective unit tests, integration tests, and use Rust's built-in testing framework. You'll learn testing best practices and understand why comprehensive testing is crucial for reliable software development.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 11: Writing Automated Tests
- Chapter 11.1: How to Write Tests
- Chapter 11.2: Controlling How Tests Are Run
- Chapter 11.3: Test Organization
Pre-lecture Reflections
- Why is testing important in software development, especially in systems programming?
- How does Rust's testing framework compare to testing frameworks you've used in other languages?
- What is the difference between unit tests, integration tests, and documentation tests?
- What makes a good test case?
Learning Objectives
By the end of this module, you will be able to:
- Write unit tests using Rust's testing framework
- Use assertions effectively in tests
- Organize and run test suites
- Understand testing best practices and test-driven development
Tests
- Why are tests useful?
- What is typical test to functional code ratio?
730K lines of code in Meta proxy server, roughly 1:1 ratio of tests to actual code. https://github.com/facebook/proxygen
Creating a Library Crate
You can use cargo to create a library project:
$ cargo new adder --lib
Created library `adder` project
$ cd adder
This will create a new project in the adder directory with the following structure:
.
├── Cargo.lock
├── Cargo.toml
└── src
└── lib.rs
Library Crate Code
Similar to the "Hello, world!" binary crate, the library crate is prepopulated with some minimal code.
pub fn add(left: u64, right: u64) -> u64 {
left + right
}
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn it_works() {
let result = add(2, 2);
assert_eq!(result, 4);
}
}-
The
#[cfg(test)]attribute tells Rust to compile and run the tests only when you runcargo test. -
The
use super::*;line tells Rust to bring all the items defined in the outer scope into the scope of the tests module. -
The
#[test]attribute tells Rust that the function is a test function. -
The
assert_eq!(result, 4);line tells Rust to check that the result of theaddfunction is equal to 4.- assert! is a macro that takes a boolean expression and panics if the expression is false.
- there are many other assert! macros, including assert_ne!, assert_approx_eq!, etc.
Running the Tests
You can run the tests with the cargo test command.
% cargo test
Compiling adder v0.1.0 (...path_to_adder/adder)
Finished `test` profile [unoptimized + debuginfo] target(s) in 0.50s
Running unittests src/lib.rs (target/debug/deps/adder-1dfa21403f25b3c4)
running 1 test
test tests::it_works ... ok
test result: ok. 1 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s
Doc-tests adder
running 0 tests
test result: ok. 0 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s
0 ignoredmeans no tests were ignored with the#[ignore]attribute.0 measuredmeans no tests were measured with Rust's built-in benchmarking framework.0 filtered outmeans no subset of tests were specified- Doc-tests automatically test any example code that is provided in
///comments.
Example Unit Test Code
Here is an example of a set of tests for a function that doubles the elements of a vector.
fn doubleme(inp: &Vec<f64>) -> Vec<f64> { let mut nv = inp.clone(); for (i, x) in inp.iter().enumerate() { nv[i] = *x * 2.0; } nv } #[test] fn test_doubleme_positive() { let v = vec![1.0, 2.0, 3.0]; let w = doubleme(&v); for (x, y) in v.iter().zip(w.iter()) { assert_eq!(*y, 2.0 * *x, "Element is not double"); } } #[test] fn test_doubleme_negative() { let v = vec![-1.0, -2.0, -3.0]; let w = doubleme(&v); for (x, y) in v.iter().zip(w.iter()) { assert_eq!(*y, 2.0 * *x, "Negative element is not double"); } } #[test] fn test_doubleme_zero() { let v = vec![0.0]; let w = doubleme(&v); for (x, y) in v.iter().zip(w.iter()) { assert_eq!(*y, 2.0 * *x, "Zero element is not double"); } } #[test] fn test_doubleme_empty() { let v: Vec<f64> = vec![]; let w = doubleme(&v); assert_eq!(w.len(), 0, "Empty Vector is not empty"); } fn testme() { let v: Vec<f64> = vec![2.0, 3.0, 4.0]; let w = doubleme(&v); println!("V = {:?} W = {:?}", v, w); } fn main() { testme(); }
Further Reading
Read 11.1 How to Write Tests for more information.
In-Class Activity
In this activity, you will write tests for a function that finds the second largest element in a slice of integers.
Be creative with your tests! With the right tests, you will be able to find the bug in the function.
Fix the bug in the function so all tests pass.
Part 1: Create a New Library Project
Create a new Rust library project:
cargo new --lib testing_practice
cd testing_practice
Part 2: Implement and Test
Replace the contents of src/lib.rs with the following function:
/// Returns the second largest element in a slice of integers.
/// Returns None if there are fewer than 2 distinct elements.
///
/// # Examples
/// ```
/// use testing_practice::second_largest;
/// assert_eq!(second_largest(&[1, 2, 3]), Some(2));
/// assert_eq!(second_largest(&[5, 5, 5]), None);
/// ```
pub fn second_largest(numbers: &[i32]) -> Option<i32> {
if numbers.len() < 2 {
return None;
}
let mut largest = numbers[0];
let mut second = numbers[1];
if second > largest {
std::mem::swap(&mut largest, &mut second);
}
for &num in &numbers[2..] {
if num > largest {
second = largest;
largest = num;
} else if num > second {
second = num;
}
}
if largest == second {
None
} else {
Some(second)
}
}
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn test_all_same() {
let result = second_largest(&[1, 1, 1]);
assert_eq!(result, None);
}
}Part 3: Write Tests
Your task is to write at least 3-4 comprehensive tests for this function. Think about:
- Normal cases
- Edge cases (empty, single element, etc.)
- Special cases (all same values, duplicates of largest, etc.)
Add your tests in a #[cfg(test)] module below the function.
Part 4: Debug
Run cargo test. If any of your tests fail, there is a bug in the function.
Your goal is to:
- Identify what test case reveals the bug
- Understand why the function fails
- Fix the function so all tests pass
Hint: Think carefully about what happens when the largest element appears multiple times in the array.
Part 5: Submit
Submit your code to Gradescope.
Generics: Avoiding Code Duplication for Different Types
About This Module
This module introduces Rust's powerful generics system, which allows writing flexible, reusable code that works with multiple types while maintaining type safety and performance. You'll learn how to create generic functions, structs, and methods, as well as understand key built-in generic types like Option<T> and Result<T, E>.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 10.1: Generic Data Types
- Chapter 10.2: Traits (for understanding trait bounds)
- Chapter 6.1: Defining an Enum (for Option
review) - Chapter 9.2: Recoverable Errors with Result (for Result<T, E> review)
Pre-lecture Reflections
- How do generics in Rust compare to similar features in languages you know (templates in C++, generics in Java)?
- What are the performance implications of Rust's monomorphization approach?
- Why might
Option<T>be safer than null values in other languages? - When would you choose
Result<T, E>overOption<T>?
Learning Objectives
By the end of this module, you will be able to:
- Write generic functions and structs using type parameters
- Apply trait bounds to constrain generic types
- Use
Option<T>andResult<T, E>for safe error handling - Understand monomorphization and its performance benefits
How python handles argument types
Python is dynamically typed and quite flexible in this regard. We can pass many different types to a function.
def max(x,y):
return x if x > y else y
>>> max(3,2)
3
>>> max(3.1,2.2)
3.1
>>> max('s', 't')
't'
Very flexible! Any downsides?
- Requires inferring types each time function is called
- Incurs runtime penalty
- No compile-time guarantees about type safety
>>> max('s',5)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<stdin>", line 2, in max
TypeError: '>' not supported between instances of 'str' and 'int'
Rust without generics
Rust is strongly typed, so we would have to create a version of the function for each type.
fn max_i32(x:i32,y:i32) -> i32 { if x > y {x} else {y} } fn max_f64(x:f64,y:f64) -> f64 { if x > y {x} else {y} } fn max_char(x:char,y:char) -> char { if x > y {x} else {y} } fn main() { println!("{}", max_i32(3,8)); println!("{}", max_f64(3.3,8.1)); println!("{}", max_char('a','b')); }
Rust Generics
Generics allow us to write one version of a function and then have the compiler generate versions for different types.
The process of going from one to the other is monomorphization.
GENERIC SOURCE COMPILER OUTPUT (roughly)
┌─────────────────┐ ┌─────────────────────┐
│ fn pass<T>(x:T) │ ────────► │ fn pass_i32(x:i32) │
│ { ... } │ │ fn pass_f64(x:f64) │
│ │ │ fn pass_char(x:char)│
└─────────────────┘ └─────────────────────┘
One source Multiple functions
Rust Generics: Syntax
Use the <T> syntax to indicate that the function is generic.
The T is a placeholder for the type and could be any character.
fn passit<T>(x:T) -> T { x } fn main() { let x = passit(5); println!("x is {x}"); let x = passit(1.1); println!("x is {x}"); let x = passit('s'); println!("x is {x}"); }
Watch Out!
Let's try this:
// ERROR -- this doesn't work fn show<T>(x:T,y:T){ println!("x is {x} and y is {y}"); } fn main() { show(3,5); show(1.1, 2.1); show('s', 't'); }
The Rust compiler is thorough enough to recognize that not all generic type may have the behavior we want.
The Fix: Trait Bounds
We can place restrictions on the generic types we would support.
fn show<T: std::fmt::Display>(x:T,y:T){ println!("x is {x} and y is {y}"); } fn main() { show(3,5); show(1.1, 2.1); show('s', 't'); show( "hello", "world"); show( true, false); //show( vec![1,2,3], vec![4,5,6]); // doesn't work }
We'll talk about traits in the next module.
Another Watch Out!
// ERROR -- similarly we could try this, but it doesn't work fn max<T>(x:T,y:T) -> T { if x > y {x} else {y} } fn main() { println!("{}", max(3,8)); println!("{}", max(3.3,8.1)); println!("{}", max('a','b')); }
Not all types support the > operator.
The Fix: Trait Bounds
We can further restrict the type of T to only allow types that implement the
PartialOrd trait.
// add info that elements of T are comparable fn max<T:PartialOrd>(x:T,y:T) -> T { if x > y {x} else {y} } fn main() { println!("{}",max(3,8)); println!("{}",max(3.3,8.1)); println!("{}",max('a','b')); }
Generics / Generic data types
In other programming languages:
- C++: templates
- Java: generics
- Go: generics
- ML, Haskell: parametric polymorphism
Generic Structs
We can define a struct that is generic.
#[derive(Debug)] struct Point<T> { x: T, y: T, } fn main() { let point_int = Point {x: 2, y: 3}; println!("{:?}", point_int); let point_float = Point {x: 4.2, y: 3.0}; println!("{:?}", point_float); }
Struct contructor method
We can define methods in the context of Structs that support generic data types
impl<T> Point<T> means that this is an implementation block and all the methods
are implemented for any type T that Point might be instantiated with.
#[derive(Debug)] struct Point<T> { x: T, y: T, } // define a constructor method for the Point struct impl<T> Point<T> { fn create(x:T,y:T) -> Point<T> { Point{x,y} } } fn main() { // create instances of the Point struct using the constructor method let point = Point::create(1, 2); let point2 = Point::<char>::create('c','d'); let point3 : Point<char> = Point::create('e','f'); println!("{:?} {:?} {:?}", point, point2, point3); }
Struct swap method
Let's implement another method that operates on an instance of the struct,
hence the use of &mut self.
Remember, &mut self means that the method is allowed to modify the instance of
the struct.
#[derive(Debug)] struct Point<T> { x: T, y: T, } // define a constructor method for the Point struct impl<T> Point<T> { fn create(x:T,y:T) -> Point<T> { Point{x,y} } } // implement a method that swaps the x and y values impl<T:Copy> Point<T> { fn swap(&mut self) { let z = self.x; self.x = self.y; self.y = z; } } fn main() { let mut point = Point::create(2,3); println!("{:?}",point); point.swap(); println!("{:?}",point); }
impl<T:Copy> specifies that T must implement the Copy trait.
You can see what happens if we remove the Copy trait.
Question: What datatype might not implement the Copy trait?
Specialized versions
Even though we have generic functions defined, we can still specify methods/functions for specific types.
#[derive(Debug)] struct Point<T> { x: T, y: T, } // define a constructor method for the Point struct impl<T> Point<T> { fn create(x:T,y:T) -> Point<T> { Point{x,y} } } impl Point<i32> { fn do_you_use_f64(&self) -> bool { false } } impl Point<f64> { fn do_you_use_f64(&self) -> bool { true } } fn main() { let p_i32 = Point::create(2,3); println!("p_i32 uses f64? {}",p_i32.do_you_use_f64()); let p_f64 = Point::create(2.1,3.1); println!("p_f64 uses f64? {}",p_f64.do_you_use_f64()); }
Useful predefined generic data types
There are two useful predefined generic data types: Option<T> and Result<T, E>.
Enum Option<T>
There is a built-in enum
Option<T>
in the standard library with two variants:
Some(T)-- The variantSomecontains a value of typeTNone
Useful for when there may be no output
- Compared to
Noneornullin other programming languages:- Rust forces handling of this case
From Option enum advantage over null:
The Option type encodes the very common scenario in which a value could be something or it could be nothing.
For example, if you request the first item in a non-empty list, you would get a value. If you request the first item in an empty list, you would get nothing.
Expressing this concept in terms of the type system means the compiler can check whether you’ve handled all the cases you should be handling;
This functionality can prevent bugs that are extremely common in other programming languages.

Example: Prime Number Finding
Here's example prime number finding code that returns Option<u32> if a prime number is found, or None if not.
fn prime(x:u32) -> bool { if x <= 1 { return false;} // factors would come in pairs. if one factor is > sqrt(x), then // the other factor must be < sqrt(x). // So we only have to search up to sqrt(x) for i in 2..=((x as f64).sqrt() as u32) { if x % i == 0 { // can be divided by i without a remainder -> not prime return false; } } true } fn prime_in_range(a:u32,b:u32) -> Option<u32> { // returns an Option<u32> for i in a..=b { if prime(i) {return Some(i);} } None } fn main() { println!("prime in 90-906? {:?}",prime_in_range(90,906)); println!("prime in 90-92? {:?}",prime_in_range(90,92)); let tmp : Option<u32> = prime_in_range(830,856); println!("prime in 830-856? {:?}",tmp); }
- If a prime number is found, it returns
Some(u32)variant with the prime number. - If the prime number is not found, it returns
None.
Extracting the content of Some(...)
There are various ways to extract the content of Some(...)
if letmatchunwrap()
fn prime(x:u32) -> bool { if x <= 1 { return false;} // factors would come in pairs. if one factor is > sqrt(x), then // the other factor must be < sqrt(x). // So we only have to search up to sqrt(x) for i in 2..=((x as f64).sqrt() as u32) { if x % i == 0 { // can be divided by i without a remainder -> not prime return false; } } true } fn prime_in_range(a:u32,b:u32) -> Option<u32> { // returns an Option<u32> for i in a..=b { if prime(i) {return Some(i);} } None } fn main() { let tmp : Option<u32> = prime_in_range(830,856); // extracting the content of Some(...) if let Some(x) = tmp { println!("{}",x); } match tmp { Some(x) => println!("{}",x), None => println!("None"), }; println!("Another way {}", tmp.unwrap()) }
Be careful with unwrap()
Be careful with unwrap(), it will crash the program if the value is None.
//ERROR fn main() { // extracting the content of Some(...) let tmp: Option<u32> = None; // try changing this to Some(3) if let Some(x) = tmp { println!("{}",x); // will skip this block if tmp is None } match tmp { Some(x) => println!("{}",x), None => println!("{:?}", tmp), }; // Boom!!!!! Will crash the program if tmp is None println!("Another way {}", tmp.unwrap()) }
Interesting related fact: Bertrand's postulate
There is always a prime number in . See Prime Number Theorem
Enum Option<T>: useful methods
Check the variant
.is_some() -> bool.is_none() -> bool
Get the value in Some or terminate with an error
.unwrap() -> T.expect(message) -> T
Get the value in Some or a default value
.unwrap_or(default_value:T) -> T
#![allow(unused)] fn main() { let x = Some(3); println!("x is some? {}",x.is_some()); }
If exception, print a message.
#![allow(unused)] fn main() { // Try line 3 instead of 4 //let x:Option<u32> = Some(3); let x = None; let y:u32 = x.expect("This should have been an integer!!!"); println!("y is {}",y); }
A better way to handle this is to use unwrap_or().
#![allow(unused)] fn main() { let x = None; println!("{}",x.unwrap_or(0)); let y = Some(3); println!("{}",y.unwrap_or(0)); }
More details:
- https://doc.rust-lang.org/std/option/
- https://doc.rust-lang.org/std/option/enum.Option.html
Enum Result<T, E>
Another built-in enum
Result<T, E>
in the standard library with two variants:
Ok(T)Err(E)
Useful when you want to pass a solution or information about an error.
fn divide(a:u32,b:u32) -> Result<u32,String> { match b { 0 => Err(String::from("Division by zero")), _ => Ok(a / b) } } fn main() { println!("{:?}",divide(3,0)); println!("{:?}",divide(2022,3)); }
Enum Result<T, E>: useful methods
Check the variant
.is_ok() -> bool.is_err() -> bool
Get the value in Ok or terminate with an error
.unwrap() -> T.expect(message) -> T
Get the value in Ok or a default value
.unwrap_or(default_value:T) -> T
#![allow(unused)] fn main() { let r1 : Result<i32,()> = Ok(3); println!("{}",r1.is_err()); println!("{}",r1.is_ok()); println!("{}",r1.unwrap()); }
But again, that will crash the program if the value is Err, so use unwrap_or().
#![allow(unused)] fn main() { let r2 : Result<u32,()> = Err(()); let r3 : Result<u32,()> = Ok(123); println!("r2: {}\nr3: {}", r2.unwrap_or(0), r3.unwrap_or(0)); }
More details:
- https://doc.rust-lang.org/std/result/
- https://doc.rust-lang.org/std/result/enum.Result.html
In-Class Poll
Will be opened and made visible in class.
In-Class Activity: Practicing Generics
Time: 10 minutes
Instructions
Work individually or in pairs. Complete as many exercises as you can in 10 minutes. You can test your code in the Rust playground or in your local environment.
Exercise 1: Fix the Generic Function (3 minutes)
The following code doesn't compile. Fix it by adding the appropriate trait bound(s).
// TODO: Fix this function so it compiles fn compare_and_print<T>(a: T, b: T) { if a > b { println!("{} is greater than {}", a, b); } else { println!("{} is less than or equal to {}", a, b); } } fn main() { compare_and_print(10, 5); compare_and_print(2.71, 3.14); compare_and_print('z', 'a'); }
Hint
You need TWO trait bounds:
- One to enable comparison (
>) - One to enable printing with
{}
Exercise 2: Complete the Generic Struct (4 minutes)
Complete the Container<T> struct by implementing the missing methods.
#[derive(Debug)] struct Container<T> { value: T, } impl<T> Container<T> { // TODO: Implement a constructor that creates a new Container fn new(value: T) -> Container<T> { // Your code here } // TODO: Implement a method that returns a reference to the value fn get(&self) -> &T { // Your code here } // TODO: Implement a method that replaces the value and returns the old one fn replace(&mut self, new_value: T) -> T { // Your code here } } fn main() { let mut container = Container::new(42); println!("Value: {:?}", container.get()); let old_value = container.replace(100); println!("Old value: {}, New value: {:?}", old_value, container.get()); }
Hint for replace()
Use std::mem::replace(&mut self.value, new_value) or swap manually using a temporary variable.
Exercise 3: Use Option (3 minutes)
Implement a function that finds the first even number in a vector. Return Some(number) if found, or None if no even numbers exist.
// TODO: Implement this function fn find_first_even(numbers: &Vec<i32>) -> Option<i32> { // Your code here } fn main() { let numbers1 = vec![1, 3, 5, 7]; let numbers2 = vec![1, 3, 6, 7]; match find_first_even(&numbers1) { Some(n) => println!("Found even number: {}", n), None => println!("No even numbers found"), } // TODO: Use unwrap_or() to print the result with a default value of -1 println!("First even in numbers2: {}", /* your code here */); }
Bonus Challenge (if you finish early)
Combine everything you learned! Create a generic Pair<T, U> struct that can hold two values of different types, and implement a method swap() that returns a new Pair<U, T> with the values swapped.
// TODO: Define the struct and implement the method struct Pair<T, U> { // Your code here } impl<T, U> Pair<T, U> { fn new(first: T, second: U) -> Self { // Your code here } fn swap(self) -> Pair<U, T> { // Your code here } } fn main() { let pair = Pair::new(42, "hello"); let swapped = pair.swap(); // This should compile and show that types are swapped! }
Solutions
Click to reveal solutions (try on your own first!)
Exercise 1 Solution
fn compare_and_print<T: PartialOrd + std::fmt::Display>(a: T, b: T) { if a > b { println!("{} is greater than {}", a, b); } else { println!("{} is less than or equal to {}", a, b); } } fn main() { compare_and_print(10, 5); compare_and_print(2.71, 3.14); compare_and_print('z', 'a'); }
Exercise 2 Solution
#[derive(Debug)] struct Container<T> { value: T, } impl<T> Container<T> { fn new(value: T) -> Container<T> { Container { value } } fn get(&self) -> &T { &self.value } fn replace(&mut self, new_value: T) -> T { std::mem::replace(&mut self.value, new_value) } } fn main() { let mut container = Container::new(42); println!("Value: {:?}", container.get()); let old_value = container.replace(100); println!("Old value: {}, New value: {:?}", old_value, container.get()); }
Exercise 3 Solution
fn find_first_even(numbers: &Vec<i32>) -> Option<i32> { for &num in numbers { if num % 2 == 0 { return Some(num); } } None } fn main() { let numbers1 = vec![1, 3, 5, 7]; let numbers2 = vec![1, 3, 6, 7]; match find_first_even(&numbers1) { Some(n) => println!("Found even number: {}", n), None => println!("No even numbers found"), } println!("First even in numbers2: {}", find_first_even(&numbers2).unwrap_or(-1)); }
Bonus Solution
#[derive(Debug)] struct Pair<T, U> { first: T, second: U, } impl<T, U> Pair<T, U> { fn new(first: T, second: U) -> Self { Pair { first, second } } fn swap(self) -> Pair<U, T> { Pair { first: self.second, second: self.first, } } } fn main() { let pair = Pair::new(42, "hello"); let swapped = pair.swap(); // This should compile and show that types are swapped! }
Traits: Defining Shared Behavior
About This Module
This module introduces Rust's trait system, which allows you to define shared behavior that can be implemented by different types. Traits are similar to interfaces in other languages but more powerful, enabling polymorphism, generic programming, and code reuse while maintaining Rust's safety guarantees.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 10.2: Traits: Defining Shared Behavior
- Chapter 17.2: Using Trait Objects That Allow for Values of Different Types
- Chapter 19.3: Advanced Traits
Pre-lecture Reflections
- How do traits in Rust compare to interfaces in Java or abstract base classes in Python?
- What are the benefits of default method implementations in traits?
- When would you use
impl Traitvs generic type parameters with trait bounds? - How do trait objects enable dynamic polymorphism in Rust?
Learning Objectives
By the end of this module, you will be able to:
- Define and implement traits for custom types
- Use trait bounds to constrain generic functions
- Understand different syntaxes for trait parameters (
impl Trait, generic bounds,whereclauses) - Return types that implement traits
Traits
From Traits: Defining Shared Behavior.
- A trait defines the functionality a particular type has and can share with other types.
- We can use traits to define shared behavior in an abstract way.
- We can use trait bounds to specify that a generic type can be any type that has certain behavior.
Some other programming languages call this an interface.
Sample trait definition
The general idea is:
-
define method signatures as behaviors that need to be implemented by any type that implements the trait
-
We can also define default implementations of methods.
#![allow(unused)] fn main() { trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } }
Sample trait implementation 1
Let's look at a simple example of a trait implementation.
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct SoccerPlayer { name: String, age: u32, team: String, } // Implement the `Person` trait for `SoccerPlayer` so that // it can be used as a `Person` object. impl Person for SoccerPlayer { fn get_age(&self) -> u32 { self.age } // We must implement all trait items fn get_name(&self) -> String { self.name.clone() } } // Implement a constructor for `SoccerPlayer` impl SoccerPlayer { fn create(name:String, age:u32, team:String) -> SoccerPlayer { SoccerPlayer{name,age,team} } } // Since `SoccerPlayer` implements the `Person` trait, // we can use the `description` method on instances of `SoccerPlayer`. fn main() { let zlatan = SoccerPlayer::create(String::from("Zlatan Ibrahimovic"), 40, String::from("AC Milan")); println!("{}", zlatan.description()); }
Sample trait implementation 2
Now let's look at another example of a trait implementation.
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct RegularPerson { year_born: u32, first_name: String, middle_name: String, last_name: String, } impl Person for RegularPerson { fn get_age(&self) -> u32 { 2024 - self.year_born } fn get_name(&self) -> String { if self.middle_name == "" { format!("{} {}",self.first_name,self.last_name) } else { format!("{} {} {}",self.first_name,self.middle_name,self.last_name) } } } impl RegularPerson { fn create(first_name:String,middle_name:String,last_name:String,year_born:u32) -> RegularPerson { RegularPerson{first_name,middle_name,last_name,year_born} } } fn main() { let mlk = RegularPerson::create( String::from("Martin"), String::from("Luther"), String::from("King"), 1929 ); println!("{}", mlk.description()); }
Using traits in functions -- Trait Bounds
So now, we specify that we need a function that accepts an object that implements the Person trait.
#![allow(unused)] fn main() { // sample function accepting object implementing trait fn long_description(person: &impl Person) { println!("{}, who is {} years old", person.get_name(), person.get_age()); } }
This way we know we can call the get_name and get_age methods on the object that is passed to the function.
It allows us to specify a whole class of objects and know what methods are available on them.
Examples
We can see this in action with the two examples we saw earlier.
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct SoccerPlayer { name: String, age: u32, team: String, } // Implement the `Person` trait for `SoccerPlayer` so that // it can be used as a `Person` object. impl Person for SoccerPlayer { fn get_age(&self) -> u32 { self.age } // We must implement all trait items fn get_name(&self) -> String { self.name.clone() } } // Implement a constructor for `SoccerPlayer` impl SoccerPlayer { fn create(name:String, age:u32, team:String) -> SoccerPlayer { SoccerPlayer{name,age,team} } } #[derive(Debug)] struct RegularPerson { year_born: u32, first_name: String, middle_name: String, last_name: String, } impl Person for RegularPerson { fn get_age(&self) -> u32 { 2024 - self.year_born } fn get_name(&self) -> String { if self.middle_name == "" { format!("{} {}",self.first_name,self.last_name) } else { format!("{} {} {}",self.first_name,self.middle_name,self.last_name) } } } impl RegularPerson { fn create(first_name:String,middle_name:String,last_name:String,year_born:u32) -> RegularPerson { RegularPerson{first_name,middle_name,last_name,year_born} } } // sample function accepting object implementing trait fn long_description(person: &impl Person) { println!("{}, who is {} years old", person.get_name(), person.get_age()); } fn main() { let mlk = RegularPerson::create( String::from("Martin"), String::from("Luther"), String::from("King"), 1929 ); let zlatan = SoccerPlayer::create(String::from("Zlatan Ibrahimovic"), 40, String::from("AC Milan")); long_description(&mlk); // we can pass a `RegularPerson` object to the function long_description(&zlatan); // we can pass a `SoccerPlayer` object to the function }
Using traits in functions: long vs. short form
There's a longer, generic version of the function that we can use.
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct SoccerPlayer { name: String, age: u32, team: String, } // Implement the `Person` trait for `SoccerPlayer` so that // it can be used as a `Person` object. impl Person for SoccerPlayer { fn get_age(&self) -> u32 { self.age } // We must implement all trait items fn get_name(&self) -> String { self.name.clone() } } // Implement a constructor for `SoccerPlayer` impl SoccerPlayer { fn create(name:String, age:u32, team:String) -> SoccerPlayer { SoccerPlayer{name,age,team} } } #[derive(Debug)] struct RegularPerson { year_born: u32, first_name: String, middle_name: String, last_name: String, } impl Person for RegularPerson { fn get_age(&self) -> u32 { 2024 - self.year_born } fn get_name(&self) -> String { if self.middle_name == "" { format!("{} {}",self.first_name,self.last_name) } else { format!("{} {} {}",self.first_name,self.middle_name,self.last_name) } } } impl RegularPerson { fn create(first_name:String,middle_name:String,last_name:String,year_born:u32) -> RegularPerson { RegularPerson{first_name,middle_name,last_name,year_born} } } // short version fn long_description(person: &impl Person) { println!("{}, who is {} old", person.get_name(), person.get_age()); } // longer version fn long_description_2<T: Person>(person: &T) { println!("{}, who is {} old", person.get_name(), person.get_age()); } fn main() { let mlk = RegularPerson::create( String::from("Martin"), String::from("Luther"), String::from("King"), 1929 ); let zlatan = SoccerPlayer::create(String::from("Zlatan Ibrahimovic"), 40, String::from("AC Milan")); long_description(&zlatan); long_description_2(&zlatan); long_description(&mlk); long_description_2(&mlk); }
So what's up with the different ways to specify traits (It's complicated!!!!)
Optional: You can skip this if you want.
&impl and &T-> static dispatch (also relevant in the context of return values)&Trestricts the type especially if you plan to pass multiple arguments of the same type (relevant to inputs)- Read https://joshleeb.com/posts/rust-traits-and-trait-objects if you want to dig deep but without a background in programming languages and compilers this will not be possible to understand.
Using traits in functions: multiple traits
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct SoccerPlayer { name: String, age: u32, team: String, } // Implement the `Person` trait for `SoccerPlayer` so that // it can be used as a `Person` object. impl Person for SoccerPlayer { fn get_age(&self) -> u32 { self.age } // We must implement all trait items fn get_name(&self) -> String { self.name.clone() } } // Implement a constructor for `SoccerPlayer` impl SoccerPlayer { fn create(name:String, age:u32, team:String) -> SoccerPlayer { SoccerPlayer{name,age,team} } } #[derive(Debug)] struct RegularPerson { year_born: u32, first_name: String, middle_name: String, last_name: String, } impl Person for RegularPerson { fn get_age(&self) -> u32 { 2024 - self.year_born } fn get_name(&self) -> String { if self.middle_name == "" { format!("{} {}",self.first_name,self.last_name) } else { format!("{} {} {}",self.first_name,self.middle_name,self.last_name) } } } impl RegularPerson { fn create(first_name:String,middle_name:String,last_name:String,year_born:u32) -> RegularPerson { RegularPerson{first_name,middle_name,last_name,year_born} } } // sample function accepting object implementing trait fn long_description(person: &impl Person) { println!("{}, who is {} years old", person.get_name(), person.get_age()); } use std::fmt::Debug; fn multiple_1(person: &(impl Person + Debug)) { println!("{:?}",person); println!("Age: {}",person.get_age()); } fn main() { let mlk = RegularPerson::create( String::from("Martin"), String::from("Luther"), String::from("King"), 1929 ); let zlatan = SoccerPlayer::create(String::from("Zlatan Ibrahimovic"), 40, String::from("AC Milan")); multiple_1(&zlatan); multiple_1(&mlk); }
Using traits in functions: multiple traits
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct SoccerPlayer { name: String, age: u32, team: String, } // Implement the `Person` trait for `SoccerPlayer` so that // it can be used as a `Person` object. impl Person for SoccerPlayer { fn get_age(&self) -> u32 { self.age } // We must implement all trait items fn get_name(&self) -> String { self.name.clone() } } // Implement a constructor for `SoccerPlayer` impl SoccerPlayer { fn create(name:String, age:u32, team:String) -> SoccerPlayer { SoccerPlayer{name,age,team} } } #[derive(Debug)] struct RegularPerson { year_born: u32, first_name: String, middle_name: String, last_name: String, } impl Person for RegularPerson { fn get_age(&self) -> u32 { 2024 - self.year_born } fn get_name(&self) -> String { if self.middle_name == "" { format!("{} {}",self.first_name,self.last_name) } else { format!("{} {} {}",self.first_name,self.middle_name,self.last_name) } } } impl RegularPerson { fn create(first_name:String,middle_name:String,last_name:String,year_born:u32) -> RegularPerson { RegularPerson{first_name,middle_name,last_name,year_born} } } // sample function accepting object implementing trait fn long_description(person: &impl Person) { println!("{}, who is {} years old", person.get_name(), person.get_age()); } use std::fmt::Debug; // three options, useful for different settings // This is good if you want to pass many parameters to the function // and the parameters are of different types fn multiple_1(person: &(impl Person + Debug)) { println!("{:?}",person); println!("Age: {}",person.get_age()); } // This is better if you want all your parameters to be of the same type fn multiple_2<T: Person + Debug>(person: &T) { println!("{:?}",person); println!("Age: {}",person.get_age()); } // This is like option 2 but easier to read if your parameter // combines many traits fn multiple_3<T>(person: &T) where T: Person + Debug { println!("{:?}",person); println!("Age: {}",person.get_age()); } fn main() { let mlk = RegularPerson::create( String::from("Martin"), String::from("Luther"), String::from("King"), 1929 ); multiple_1(&mlk); multiple_2(&mlk); multiple_3(&mlk); }
Returning types implementing a trait
trait Person { // method header specifications // must be implemented by any type that implements the trait fn get_name(&self) -> String; fn get_age(&self) -> u32; // default implementation of a method fn description(&self) -> String { format!("{} ({})",self.get_name(),self.get_age()) } } #[derive(Debug)] struct SoccerPlayer { name: String, age: u32, team: String, } // Implement the `Person` trait for `SoccerPlayer` so that // it can be used as a `Person` object. impl Person for SoccerPlayer { fn get_age(&self) -> u32 { self.age } // We must implement all trait items fn get_name(&self) -> String { self.name.clone() } } // Implement a constructor for `SoccerPlayer` impl SoccerPlayer { fn create(name:String, age:u32, team:String) -> SoccerPlayer { SoccerPlayer{name,age,team} } } #[derive(Debug)] struct RegularPerson { year_born: u32, first_name: String, middle_name: String, last_name: String, } impl Person for RegularPerson { fn get_age(&self) -> u32 { 2024 - self.year_born } fn get_name(&self) -> String { if self.middle_name == "" { format!("{} {}",self.first_name,self.last_name) } else { format!("{} {} {}",self.first_name,self.middle_name,self.last_name) } } } impl RegularPerson { fn create(first_name:String,middle_name:String,last_name:String,year_born:u32) -> RegularPerson { RegularPerson{first_name,middle_name,last_name,year_born} } } // sample function accepting object implementing trait fn long_description(person: &impl Person) { println!("{}, who is {} years old", person.get_name(), person.get_age()); } fn get_zlatan() -> impl Person { SoccerPlayer::create(String::from("Zlatan Ibrahimovic"), 40, String::from("AC Milan")) } fn main() { let zlatan = SoccerPlayer::create(String::from("Zlatan Ibrahimovic"), 40, String::from("AC Milan")); let zlatan_2 = get_zlatan(); long_description(&zlatan_2); }
Recap
- Traits are a way to define shared behavior that can be implemented by different types.
- We can use traits to define shared behavior in an abstract way.
- We can use trait bounds to specify that a generic type can be any type that has certain behavior.
In-Class Activity: Practicing Traits and Trait Bounds
Time: 10 minutes
Instructions
Work individually or in pairs. Complete as many exercises as you can in 10 minutes. You can test your code in the Rust playground or in your local environment.
Exercise 1: Define and Implement a Trait (3 minutes)
Define a trait called Describable with a method describe() that returns a String. Then implement it for the Book struct.
// TODO: Define the Describable trait trait Describable { // Your code here } struct Book { title: String, author: String, pages: u32, } // TODO: Implement Describable for Book // The describe() method should return a string like: // "'The Rust Book' by Steve Klabnik (500 pages)" fn main() { let book = Book { title: String::from("The Rust Book"), author: String::from("Steve Klabnik"), pages: 500, }; println!("{}", book.describe()); }
Hint
Remember the trait definition syntax:
#![allow(unused)] fn main() { trait TraitName { fn method_name(&self) -> ReturnType; } }
And implementation:
#![allow(unused)] fn main() { impl TraitName for StructName { fn method_name(&self) -> ReturnType { // implementation } } }
Exercise 2: Multiple Trait Bounds with Where Clause (3 minutes)
Refactor the following function to use a where clause instead of inline trait bounds. Then add a call to the function in main.
use std::fmt::{Debug, Display}; // TODO: Refactor this to use a where clause fn print_info<T: Debug + Display + PartialOrd>(item: &T, compare_to: &T) { println!("Item: {}", item); println!("Debug: {:?}", item); if item > compare_to { println!("Item is greater than comparison value"); } } fn main() { // TODO: Call print_info with appropriate arguments }
Hint
The where clause syntax is:
#![allow(unused)] fn main() { fn function_name<T>(params) -> ReturnType where T: Trait1 + Trait2 { // body } }
Bonus Challenge (if you finish early)
Create a trait called Area with a method area() that returns f64. Implement it for both Circle and Rectangle structs. Then write a generic function print_area that accepts anything implementing the Area trait.
// TODO: Define the Area trait // TODO: Define Circle struct (radius: f64) // TODO: Define Rectangle struct (width: f64, height: f64) // TODO: Implement Area for Circle (π * r²) // TODO: Implement Area for Rectangle (width * height) // TODO: Write a generic function that prints the area // fn print_area(...) { ... } fn main() { let circle = Circle { radius: 5.0 }; let rectangle = Rectangle { width: 4.0, height: 6.0 }; print_area(&circle); print_area(&rectangle); }
Solutions
Click to reveal solutions (try on your own first!)
Exercise 1 Solution
trait Describable { fn describe(&self) -> String; } struct Book { title: String, author: String, pages: u32, } impl Describable for Book { fn describe(&self) -> String { format!("'{}' by {} ({} pages)", self.title, self.author, self.pages) } } fn main() { let book = Book { title: String::from("The Rust Book"), author: String::from("Steve Klabnik"), pages: 500, }; println!("{}", book.describe()); }
Exercise 2 Solution
use std::fmt::{Debug, Display}; fn print_info<T>(item: &T, compare_to: &T) where T: Debug + Display + PartialOrd { println!("Item: {}", item); println!("Debug: {:?}", item); if item > compare_to { println!("Item is greater than comparison value"); } } fn main() { print_info(&42, &10); print_info(&3.14, &2.71); print_info(&'z', &'a'); }
Bonus Solution
trait Area { fn area(&self) -> f64; } struct Circle { radius: f64, } struct Rectangle { width: f64, height: f64, } impl Area for Circle { fn area(&self) -> f64 { std::f64::consts::PI * self.radius * self.radius } } impl Area for Rectangle { fn area(&self) -> f64 { self.width * self.height } } fn print_area(shape: &impl Area) { println!("Area: {:.2}", shape.area()); } // Alternative using generic syntax: // fn print_area<T: Area>(shape: &T) { // println!("Area: {:.2}", shape.area()); // } fn main() { let circle = Circle { radius: 5.0 }; let rectangle = Rectangle { width: 4.0, height: 6.0 }; print_area(&circle); print_area(&rectangle); }
Lifetimes in Rust
About This Module
This module introduces Rust's lifetime system, which ensures memory safety by tracking how long references remain valid. We'll explore lifetime annotations, the borrow checker, lifetime elision rules, and how lifetimes work with functions, structs, and methods.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
Pre-lecture Reflections
Before class, consider these questions:
- How do lifetimes prevent dangling pointer bugs that plague other systems languages?
- When does Rust require explicit lifetime annotations vs. lifetime elision?
- How do lifetime parameters relate to generic type parameters?
- What are the trade-offs between memory safety and programming convenience in lifetime systems?
- How do lifetimes enable safe concurrent programming patterns?
Learning Objectives
By the end of this module, you should be able to:
- Understand how the borrow checker prevents dangling references
- Write explicit lifetime annotations when required by the compiler
- Apply lifetime elision rules to understand when annotations are optional
- Use lifetimes in function signatures, structs, and methods
- Combine lifetimes with generics and trait bounds
- Debug lifetime-related compilation errors effectively
Lifetimes Overview
- Ensures references are valid as long as we need them to be
- The goal is to enable Rust compiler to prevent dangling references.
- A dangling reference is a reference that points to data that has been freed or is no longer valid.
Note: you can separate declaration and initialization
#![allow(unused)] fn main() { let r; // declaration r = 32; // initialization println!("r: {r}"); }
- Consider the following code:
#![allow(unused)] fn main() { let r; { let x = 5; r = &x; } println!("r: {r}"); }
The Rust Compiler Borrow Checker
-
Let's annotate the lifetimes of
randx. -
Rust uses a special naming pattern for lifetimes:
'a(single quote followed by identifier)
#![allow(unused)] fn main() { let r; // ---------+-- 'a // | { // | let x = 5; // -+-- 'b | r = &x; // | | } // -+ | // | println!("r: {r}"); // | // ---------+ }
-
We can see that
xgoes out of scope before we use a reference,r, tox. -
We can can fix the scope so lifetimes overlap
#![allow(unused)] fn main() { let x = 5; // ----------+-- 'b // | let r = &x; // --+-- 'a | // | | println!("r: {r}"); // | | // --+ | // ----------+ }
Generic Lifetimes in Functions
-
Let's see an example of why we need to be able to specify lifetimes.
-
Say we want to compare to strings and pick the longest one
// Compiler Error // compare two string slices and return reference to the longest fn longest(x: &str, y: &str) -> &str { if x.len() > y.len() {x} else {y} } fn main() { let string1 = String::from("abcd"); let string2 = "xyz"; let result = longest(string1.as_str(), string2); println!("The longest string is {result}"); }
Why is this a problem?
Answer: In general, we don't know which reference will be returned and so we can't know the lifetime of the return reference.
The Solution: Lifetime Annotation Syntax
- names of lifetime parameters must start with an apostrophe (') and are usually all lowercase and very short, like generic types
#![allow(unused)] fn main() { &i32 // a reference with inferred lifetime &'a i32 // a reference with an explicit lifetime &'a mut i32 // a mutable reference with an explicit lifetime }
- now we can annotate our function with lifetime
#![allow(unused)] fn main() { fn longest<'a>(x: &'a str, y: &'a str) -> &'a str { if x.len() > y.len() {x} else {y} } }
Update Example with Lifetime Annotation
-
we use the same syntax like we used for generic types,
fn longest<'a>(... -
The lifetime
'ais the shorter of the two input lifetimes:(x: &'a str, y: &'a str) -
The returned string slice will have lifetime at least as long as
'a, e.g.-> &'a str
fn longest<'a>(x: &'a str, y: &'a str) -> &'a str { if x.len() > y.len() {x} else {y} } fn main() { let string1 = String::from("abcd"); let string2 = "xyz"; let result = longest(string1.as_str(), string2); println!("The longest string is {result}"); }
- Above is not an issue, because all lifetimes are the same.
Example of Valid Code
// this code is still fine fn longest<'a>(x: &'a str, y: &'a str) -> &'a str { if x.len() > y.len() {x} else {y} } fn main() { let string1 = String::from("long string is long"); { let string2 = String::from("xyz"); let result = longest(string1.as_str(), string2.as_str()); println!("The longest string is {result}"); } }
- Above is not an issue, because the returned reference is no longer than the shorter of the two args
Example of Invalid Code
- But what about below?
fn longest<'a>(x: &'a str, y: &'a str) -> &'a str { if x.len() > y.len() {x} else {y} } fn main() { let string1 = String::from("abcd"); // ----------+-- 'a let result; // | { // | let string2 = "xyz"; // --+-- 'b | result = longest(string1.as_str(), string2); // | | } // --+ | println!("The longest string is {result}"); // | } // ----------+
- We're trying to use
resultafter the shortest arg lifetime ended
Lifetime of return type must match lifetime of at least one parameter
- This won't work
#![allow(unused)] fn main() { fn first_str<'a>(_x: &str, _y: &str) -> &'a str { let result = String::from("really long string"); result.as_str() } }
Why is this a problem?
Answer: The return reference is to `result` which gets dropped at end of function.
Lifetime Annotations in Struct Definitions
-
So far, we've only used structs that fully owned their member types.
-
We can define structs to hold references, but then we need lifetime annotations
#[derive(Debug)] struct ImportantExcerpt<'a> { part: &'a str, } fn main() { let novel = String::from("Call me Ishmael. Some years ago..."); let first_sentence = novel.split('.').next().unwrap(); let i = ImportantExcerpt { part: first_sentence, }; println!("{:?}", i); }
- An instance of
ImportantExcerptcan't outlive the reference it holds in thepartfield.
Lifetime Elision
e·li·sion
/əˈliZH(ə)n/
noun
the omission of a sound or syllable when speaking (as in I'm, let's, e ' en ).
* an omission of a passage in a book, speech, or film.
"the movie's elisions and distortions have been carefully thought out"
* the process of joining together or merging things, especially abstract ideas.
"unease at the elision of so many vital questions"
- In Rust, the cases where we can omit lifetime annotations are called lifetime elision.
Lifetime Elision Example
So why does this function compile without errors?
fn first_word(s: &str) -> &str { let bytes = s.as_bytes(); for (i, &item) in bytes.iter().enumerate() { if item == b' ' { return &s[0..i]; } } &s[..] } fn main() { let s = String::from("Call me Ishmael."); let word = first_word(&s); println!("The first word is: {word}"); }
Shouldn't we have to write?
#![allow(unused)] fn main() { fn first_word<'a>(s: &'a str) -> &'a str { }
Inferring Lifetimes
The compiler developers decided that some patterns were so common and simple to infer that the compiler could just infer and automatically generate the lifetime specifications.
-
input lifetimes: lifetimes on function or method parameters
-
output lifetimes: lifetimes on return values
Three Rules for Compiler Lifetime Inference
First Rule
Assign a lifetime parameter to each parameter that is a reference.
#![allow(unused)] fn main() { // function with one parameter fn foo<'a>(x: &'a i32); //a function with two parameters gets two separate lifetime parameters: fn foo<'a, 'b>(x: &'a i32, y: &'b i32); // and so on. }
Three Rules for Compiler Lifetime Inference
Second Rule
If there is exactly one input lifetime parameter, that lifetime is assigned to all output lifetime parameters
#![allow(unused)] fn main() { fn foo<'a>(x: &'a i32) -> &'a i32 }
Three Rules for Compiler Lifetime Inference
Third Rule -- Methods
If there are multiple input lifetime parameters, but one of them is &self or &mut self because this is a method, the lifetime of self is assigned to all output lifetime parameters.
Let's Test Our Understanding
You're the compiler and you see this function.
fn first_word(s: &str) -> &str {...}Do any rules apply? which one would you apply first?
Answer:
First rule: Apply input lifetime annotations.
fn first_word<'a>(s: &'a str) -> &str {...}Second rule: Apply output lifetime annotation.
fn first_word<'a>(s: &'a str) -> &'a str {...}Done! Everything is accounted for.
Test Our Understanding Again
What about if you see this function signature?
fn longest(x: &str, y: &str) -> &str {...}Can we apply any rules?
We can apply first rule again. Each parameter gets it's own lifetime.
fn longest<'a, 'b>(x: &'a str, y: &'b str) -> &str {...}Can we apply anymore rules?
No! Produce a compiler error asking for annotations.
Lifetime Annotations in Method Definitions
Let's take a look at the third rule again:
If there are multiple input lifetime parameters, but one of them is
&selfor&mut selfbecause this is a method, the lifetime of self is assigned to all output lifetime parameters.
Previously, we defined a struct with a field that takes a string slice reference.
#![allow(unused)] fn main() { #[derive(Debug)] struct ImportantExcerpt<'a> { part: &'a str, } // For implementation, `impl` of methods, we use the generics style annotation, which is required. // But we don't have to annotate the following method. The **First Rule** applies. impl<'a> ImportantExcerpt<'a> { fn level(&self) -> i32 { 3 } } // For the following method... impl<'a> ImportantExcerpt<'a> { fn announce_and_return_part(&self, announcement: &str) -> &str { println!("Attention please: {announcement}"); self.part } } }
There are two input lifetimes so:
- Rust applies the first lifetime elision rule and gives both
&selfand announcement their own lifetimes. - Then, because one of the parameters is
&self, the return type gets the lifetime of&self, and all lifetimes have been accounted for.
The Static Lifetime
- a special lifetime designation
- lives for the entire duration of the program
#![allow(unused)] fn main() { // This is actually redundant since string literals are always 'static let s: &'static str = "I have a static lifetime."; }
-
use only if necessary
-
manage lifetimes more fine grained if at all possible
For more, see for example:
- https://doc.rust-lang.org/rust-by-example/scope/lifetime/static_lifetime.html
Combining Lifetimes with Generics and Trait Bounds
Let's look at an example that combines:
- lifetimes
- generics with trait bounds
use std::fmt::Display; fn longest_with_an_announcement<'a, T>( x: &'a str, y: &'a str, ann: T, ) -> &'a str where T: Display, // T must implement the Display trait { println!("Announcement! {ann}"); if x.len() > y.len() { x } else { y } } fn main() { let string1 = String::from("short"); let string2 = "longer"; let result = longest_with_an_announcement(string1.as_str(), string2, "Hear ye! Hear ye!"); println!("The longest string is {result}"); }
Breaking Down the Function Declaration
Let's break down the function declaration:
#![allow(unused)] fn main() { fn longest_with_an_announcement<'a, T>( x: &'a str, y: &'a str, ann: T, ) -> &'a str where T: Display, // T must implement the Display trait }
- It has two generic parameters:
'a: A lifetime parameterT: A type parameter
- It takes three arguments:
x: A string slice with lifetime'ay: A string slice with lifetime'aann: A value of generic typeT
- Returns a string slice with lifetime
'a - The
whereclause specifies that typeTmust implement theDisplaytrait
Recap
- Lifetimes are a way to ensure that references are valid as long as we need them to be.
- The borrow checker is a tool that helps us ensure that our references are valid.
- We can use lifetime annotations to help the borrow checker understand our code better.
- We can use lifetime elision to help the compiler infer lifetimes for us.
- We can use lifetimes in function signatures, structs, and methods.
- We can combine lifetimes with generics and trait bounds.
In-Class Exercise
Part 1 -- Illustrate the Lifetimes
Annotate the lifetimes of the variables in the following code using the notation from the beginning of the module.
Paste the result in GradeScope.
#![allow(unused)] fn main() { { let s = String::from("never mind how long precisely --"); // { // let t = String::from("Some years ago -- "); // { // let v = String::from("Call me Ishmael."); // println!("{v}"); // } // println!("{t}"); // } // println!("{s}"); // } // }
Solution
#![allow(unused)] fn main() { { let s = String::from("never mind how long precisely --"); //----------+'a { // | let t = String::from("Some years ago -- "); //------+'b | { // | | let v = String::from("Call me Ishmael."); //--+'c | | println!("{v}"); // | | | } //--+ | | println!("{t}"); // | | } //--------+ | println!("{s}"); // | } //----------+ }
Part 2 -- Fix the Function with Multiple References
The following function is supposed to take a vector of string slices, a default value, and an index, and return either the string at the given index or the default if the index is out of bounds. However, it won't compile without lifetime annotations.
Add the appropriate lifetime annotations to make this code compile and paste the result in GradeScope.
fn get_or_default(strings: &Vec<&str>, default: &str, index: usize) -> &str { if index < strings.len() { strings[index] } else { default } } fn main() { let vec = vec!["hello", "world", "rust"]; let default = "not found"; let result = get_or_default(&vec, default, 5); println!("{}", result); }
Solution
fn get_or_default<'a>(strings: &Vec<&'a str>, default: &'a str, index: usize) -> &'a str { if index < strings.len() { strings[index] } else { default } } fn main() { let vec = vec!["hello", "world", "rust"]; let default = "not found"; let result = get_or_default(&vec, default, 5); println!("{}", result); }
The return value could come from either strings or default, so both need the same
lifetime annotation 'a. The vector reference itself doesn't need to live as long since
we're returning references to its contents, not the vector itself.
Part 3 -- Generic Type with Lifetime Annotations
The following code defines a Wrapper struct that holds both a generic value and a
reference. The struct and its method won't compile without proper lifetime annotations.
Add the appropriate lifetime annotations to make this code compile and paste the result in GradeScope.
struct Wrapper<T> { value: T, description: &str, } impl<T> Wrapper<T> { fn new(value: T, description: &str) -> Self { Wrapper { value, description } } fn get_description(&self) -> &str { self.description } fn get_value(&self) -> &T { &self.value } } fn main() { let desc = String::from("A number"); let wrapper = Wrapper::new(42, &desc); println!("Value: {}, Description: {}", wrapper.get_value(), wrapper.get_description()); }
Solution
struct Wrapper<'a, T> { value: T, description: &'a str, } impl<'a, T> Wrapper<'a, T> { fn new(value: T, description: &'a str) -> Self { Wrapper { value, description } } fn get_description(&self) -> &str { self.description } fn get_value(&self) -> &T { &self.value } } fn main() { let desc = String::from("A number"); let wrapper = Wrapper::new(42, &desc); println!("Value: {}, Description: {}", wrapper.get_value(), wrapper.get_description()); }
The struct needs a lifetime parameter 'a because it holds a reference (description).
The impl block must also declare this lifetime parameter: impl<'a, T>. The methods
get_description and get_value don't need explicit lifetime annotations because the
compiler can apply elision rules (the return lifetime is inferred from &self).
Closures (Anonymous Functions) in Rust
About This Module
This module introduces Rust closures - anonymous functions that can capture variables from their environment. Closures are powerful tools for functional programming patterns, lazy evaluation, and creating flexible APIs. Unlike regular functions, closures can capture variables from their surrounding scope, making them ideal for customizing behavior and implementing higher-order functions.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
Pre-lecture Reflections
Before class, consider these questions:
- How do closures differ from regular functions in terms of variable capture?
- What are the advantages of lazy evaluation using closures over eager evaluation?
- How does Rust's type inference work with closure parameters and return types?
- When would you choose a closure over a function pointer for API design?
- How do closures enable functional programming patterns in systems programming?
Learning Objectives
By the end of this module, you should be able to:
- Define and use closures with various syntactic forms
- Understand how closures capture variables from their environment
- Implement lazy evaluation patterns using closures
- Use closures with Option and Result methods like unwrap_or_else
- Apply closures for HashMap entry manipulation and other standard library methods
- Choose between closures and function pointers based on use case
Closures (Anonymous Functions)
- Closures are anonymous functions you can:
- save in a variable, or
- pass as arguments to other functions
In Python they are called lambda functions:
>>> x = lambda a, b: a * b
>>> print(x(5,6))
30
In Rust syntax (with implicit or explicit type specification):
|a, b| a * b
|a: i32, b: i32| -> i32 {a * b}
Basic Closure Syntax
- types are inferred
#![allow(unused)] fn main() { // Example 1: Basic closure syntax let add = |x, y| x + y; println!("Basic closure: 5 + 3 = {}", add(5, 3)); }
Can't change types
- Once inferred, the type cannot change.
#![allow(unused)] fn main() { let example_closure = |x| x; let s = example_closure(String::from("hello")); let n = example_closure(5); }
Basic Closure Syntax with Explicit Types
- Type annotations in closures are optional unlike in functions.
- Required in functions because those are interfaces exposed to users.
For comparison:
fn add_one_v1 (x: u32) -> u32 { x + 1 } // function
let add_one_v2 = |x: u32| -> u32 { x + 1 }; // closures...
let add_one_v3 = |x| { x + 1 }; // ... remove types
let add_one_v4 = |x| x + 1 ; // ... remove bracketsAnother example:
#![allow(unused)] fn main() { let add = |x: i32, y: i32| -> i32 {x + y}; println!("Basic closure: 5 + 3 = {}", add(5, 3)); }
Closure Capturing a Variable from the Environment
Note how multiplier is used from the environment.
#![allow(unused)] fn main() { let multiplier = 2; let multiply = |x| x * multiplier; println!("Closure with captured variable: 4 * {} = {}", multiplier, multiply(4)); }
Closure with Multiple Statements
#![allow(unused)] fn main() { let process = |x: i32| { let doubled = x * 2; doubled + 1 }; println!("Multi-statement closure: process(3) = {}", process(3)); }
Digression
- You can assign regular functions to variables as well
#![allow(unused)] fn main() { fn median2(arr: &mut [i32]) -> i32 { arr.sort(); println!("{}", arr[2]); arr[2] } let f = median2; f(&mut [1,4,5,6,4]); }
- but you can't capture variables from the environment.
Lazy Evaluation
Closures enable lazy evaluation: delaying computation until the result is actually needed.
unwrap_or()andunwrap_or_else()are methods onOptionandResultunwrap_or_else()takes a closure and only executes on else case.
// Expensive computation function // What is this computing??? fn expensive_computation(n: i32) -> i32 { println!("Computing expensive result..."); if n <= 1 { 1 } else { expensive_computation(n-1) + expensive_computation(n-2) } } fn main() { let x = Some(5); // EAGER evaluation - always computed, even if not needed! println!("EAGER evaluation"); let result1 = x.unwrap_or(expensive_computation(5)); println!("Result 1: {}", result1); // LAZY evaluation - only computed if needed println!("\nLAZY evaluation"); let result2 = x.unwrap_or_else(|| expensive_computation(5)); // <-- note the closure! println!("Result 2: {}", result2); // When x is None, the closure is called println!("\nNone evaluation"); let y: Option<i32> = None; let result3 = y.unwrap_or_else(|| expensive_computation(5)); println!("Result 3: {}", result3); }
Key insight: unwrap_or_else takes a closure, delaying execution until needed.
Recap
- Closures are anonymous functions that can be saved in variables or passed as arguments
- Syntax:
|params| expressionor|params| { statements }- type annotations are optional - Type inference: Closure types are inferred from first use and cannot change afterward
- Environment capture: Unlike regular functions, closures can capture variables from their surrounding scope
- Flexibility: Closures are more flexible than functions, but functions can also be assigned to variables
- Closures enable lazy evaluation, functional programming patterns, and flexible API design
In-Class Activity
Exercise: Mastering Closures (10 minutes)
Setup: Work individually or in pairs. Open the Rust Playground or your local editor.
Paste your solutions in GradeScope.
Part 1: Basic Closure Practice (3 minutes)
Create closures for the following tasks. Try to use the most concise syntax possible:
- A closure that takes two integers and returns their maximum
- A closure that takes a string slice and returns its length
- A closure that captures a
tax_ratevariable from the environment and calculates the total price (price + tax)
fn main() { // TODO 1: Write a closure that returns the maximum of two integers let max = // YOUR CODE HERE println!("Max of 10 and 15: {}", max(10, 15)); // TODO 2: Write a closure that returns the length of a string slice let str_len = // YOUR CODE HERE println!("Length of 'hello': {}", str_len("hello")); // TODO 3: Write a closure that captures tax_rate and calculates total let tax_rate = 0.08; let calculate_total = // YOUR CODE HERE println!("Price $100 with {}% tax: ${:.2}", tax_rate * 100.0, calculate_total(100.0)); }
Part 2: Lazy vs Eager Evaluation (4 minutes)
Fix the following code by converting eager evaluation to lazy evaluation where appropriate:
fn expensive_database_query(id: i32) -> String { println!("Querying database for id {}...", id); // Simulate expensive operation format!("User_{}", id) } fn main() { // Scenario 1: We have a cached user let cached_user = Some("Alice".to_string()); // BUG: This always queries the database, even when we have a cached value! let user1 = cached_user.unwrap_or(expensive_database_query(42)); println!("User 1: {}", user1); // TODO: Fix the above to only query when needed // Scenario 2: No cached user let cached_user2: Option<String> = None; let user2 = // YOUR CODE HERE - use lazy evaluation println!("User 2: {}", user2); }
Part 3: Counter using a mutable closure
Create a closure that captures and modifies a variable and assigns
it to a variable called increment.
fn main() { // Create a counter using a mutable closure // This closure captures and modifies a variable // Your code here. println!("Count: {}", increment()); println!("Count: {}", increment()); println!("Count: {}", increment()); }
Bonus: Challenge - Functions That Accept Closures (3 minutes)
Write a function that takes a closure as a parameter and uses it:
// TODO: Complete this function that applies an operation to a number // only if the number is positive. Otherwise returns None. fn apply_if_positive<F>(value: i32, operation: F) -> Option<i32> where F: Fn(i32) -> i32 // F is a closure that takes i32 and returns i32 { // YOUR CODE HERE } fn main() { // Test with different closures let double = |x| x * 2; let square = |x| x * x; println!("Double 5: {:?}", apply_if_positive(5, double)); println!("Square 5: {:?}", apply_if_positive(5, square)); println!("Double -3: {:?}", apply_if_positive(-3, double)); }
Discussion Questions (during/after activity):
- When did you need explicit type annotations vs. relying on inference?
- In Part 2, what's the practical difference in performance between eager and lazy evaluation?
- Can you think of other scenarios where lazy evaluation with closures would be beneficial?
- What happens if you try to use a closure after the captured variable has been moved?
Solutions
Part 1 Solutions:
fn main() { // Solution 1: Maximum of two integers let max = |a, b| if a > b { a } else { b }; println!("Max of 10 and 15: {}", max(10, 15)); // Solution 2: Length of a string slice let str_len = |s: &str| s.len(); println!("Length of 'hello': {}", str_len("hello")); // Solution 3: Calculate total with captured tax_rate let tax_rate = 0.08; let calculate_total = |price| price + (price * tax_rate); println!("Price $100 with {}% tax: ${:.2}", tax_rate * 100.0, calculate_total(100.0)); }
Key Points:
- The
maxclosure uses an if expression to return the larger value - The
str_lenclosure needs a type annotation&strbecause Rust needs to know it's a string slice (not aString) - The
calculate_totalclosure capturestax_ratefrom the environment automatically
Part 2 Solutions:
fn expensive_database_query(id: i32) -> String { println!("Querying database for id {}...", id); format!("User_{}", id) } fn main() { // Scenario 1: We have a cached user let cached_user = Some("Alice".to_string()); // FIXED: Use unwrap_or_else with a closure for lazy evaluation let user1 = cached_user.unwrap_or_else(|| expensive_database_query(42)); println!("User 1: {}", user1); // Scenario 2: No cached user let cached_user2: Option<String> = None; let user2 = cached_user2.unwrap_or_else(|| expensive_database_query(99)); println!("User 2: {}", user2); }
Key Points:
- In Scenario 1, with
unwrap_or_else, the database query is NOT executed because we haveSome("Alice") - In Scenario 2, the closure IS executed because we have
None - Notice the closure syntax:
|| expensive_database_query(42)- no parameters needed - The lazy evaluation saves expensive computation when the value is already available
Part 3 Solutions:
fn main() { // Create a counter using a mutable closure // This closure captures and modifies a variable let mut count = 0; let mut increment = || { count += 1; count }; println!("Count: {}", increment()); println!("Count: {}", increment()); println!("Count: {}", increment()); }
- The closure mutates the captured variable each time it's called
Bonus: Challenge Solutions:
// Solution: Complete function that applies operation only to positive numbers fn apply_if_positive<F>(value: i32, operation: F) -> Option<i32> where F: Fn(i32) -> i32 { if value > 0 { Some(operation(value)) } else { None } } fn main() { // Test with different closures let double = |x| x * 2; let square = |x| x * x; println!("Double 5: {:?}", apply_if_positive(5, double)); // Some(10) println!("Square 5: {:?}", apply_if_positive(5, square)); // Some(25) println!("Double -3: {:?}", apply_if_positive(-3, double)); // None }
Key Points:
- The function uses a generic type parameter
Fwith aFn(i32) -> i32trait bound - This allows any closure (or function) that takes an
i32and returns ani32 - The mutable closure requires
muton bothcountandincrement - This demonstrates closure flexibility: they can be immutable (like
double) or mutable (likeincrement)
Iterators in Rust
About This Module
This module introduces Rust's iterator pattern, which provides a powerful and efficient way to process sequences of data. Iterators in Rust are lazy, meaning they don't do any work until you call methods that consume them. You'll learn to create custom iterators, use built-in iterator methods, and understand how iterators enable functional programming patterns while maintaining Rust's performance characteristics.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
- Chapter 13.2: Processing a Series of Items with Iterators
- Chapter 13.4: Comparing Performance: Loops vs. Iterators
Pre-lecture Reflections
Before class, consider these questions:
- How do iterators in Rust differ from traditional for loops in terms of performance and safety?
- What does it mean for iterators to be "lazy" and why is this beneficial?
- How do iterator adapters (like map, filter) differ from iterator consumers (like collect, fold)?
- Why can't floating-point ranges be directly iterable in Rust?
- How does implementing the Iterator trait enable custom data structures to work with Rust's iteration ecosystem?
Learning Objectives
By the end of this module, you should be able to:
- Create and use iterators from ranges and collections
- Implement custom iterators by implementing the Iterator trait
- Apply iterator adapters (map, filter, take, cycle) to transform data
- Use iterator consumers (collect, fold, reduce, any) to produce final results
- Understand lazy evaluation in the context of Rust iterators
- Choose between iterator-based and loop-based approaches for different scenarios
Iterators
The iterator pattern allows you to perform some task on a sequence of items in turn.
An iterator is responsible for the logic of iterating over each item and determining when the sequence has finished.
- provide values one by one
- method
nextprovides next one Some(value)orNoneif no more available
Some ranges are iterators:
1..1000..
First value has to be known (so .. and ..123 are not)
Range as an Iterator Example
fn main() { let mut iter = 1..3; // must be mutable println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); }
Range between floats is not iterable
- What about a range between floats?
#![allow(unused)] fn main() { let mut iter = 1.0..3.0; // must be mutable println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); }
-
In Rust, ranges over floating-point numbers (f64) are not directly iterable.
-
This is because floating-point numbers have inherent precision issues that make it difficult to guarantee exact iteration steps.
Range between characters is iterable
- But this works.
#![allow(unused)] fn main() { let mut iter = 'a'..'c'; // must be mutable println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); println!("{:?}", iter.next()); }
Iterator from Scratch: Implementing the Iterator Trait
struct Fib { current: u128, next: u128, } impl Fib { fn new() -> Fib { Fib{current: 0, next: 1} } } impl Iterator for Fib { type Item = u128; // Calculate the next number in the Fibonacci sequence fn next(&mut self) -> Option<Self::Item> { let now = self.current; self.current = self.next; self.next = now + self.current; Some(now) } } fn main() { let mut fib = Fib::new(); for _ in 0..10 { print!("{:?} ",fib.next().unwrap()); } println!(); }
Iterator Methods and Adapters
Pay special attention to what the output is.
next()-> Get the next element of an iterator (None if there isn't one)collect()-> Put iterator elements in collectiontake(N)-> take first N elements of an iterator and turn them into an iteratorcycle()-> Turn a finite iterator into an infinite one that repeats itselffor_each(||, )-> Apply a closure to each element in the iteratorfilter(||, )-> Create new iterator from old one for elements where closure is truemap(||, )-> Create new iterator by applying closure to input iteratorany(||, )-> Return true if closure is true for any element of the iteratorfold(a, |a, |, )-> Initialize expression to a, execute closure on iterator and accumulate into areduce(|x, y|, )-> Similar to fold but the initial value is the first element in the iteratorzip(iterator)-> Zip two iterators together to turn them into pairs
If the method returns an iterator, you have to do something with the iterator.
See Rust provided methods for the complete list.
Iterator Methods Examples
#![allow(unused)] fn main() { // this does nothing! let v1 = vec![1, 2, 3]; let mut v1_iter = v1.iter(); println!("{:?}", v1_iter); println!("{:?}", v1_iter.next()); }
collect can be used to put elements of an iterator into a vector:
#![allow(unused)] fn main() { let small_numbers : Vec<_> = (1..=10).collect(); println!("{:?}", small_numbers); }
take turns an infinite iterator into an iterator that provides at most a specific number of elements
#![allow(unused)] fn main() { let small_numbers : Vec<_> = (1..).take(15).collect(); println!("{:?}", small_numbers); }
cycle creates an iterator that repeats itself forever:
#![allow(unused)] fn main() { let cycle : Vec<_> = (1..4).cycle().take(21).collect(); println!("{:?}", cycle); }
Recap
- Iterators provide values one by one via the
next()method, returningSome(value)orNone - Ranges like
1..100and0..are iterators (but floating-point ranges are not) - Custom iterators can be created by implementing the
Iteratortrait withnext()method - Lazy evaluation: Iterators don't do work until consumed
- Adapters (like
map,filter,take,cycle) transform iterators into new iterators - Consumers (like
collect,fold,reduce,any) produce final results from iterators - Iterators enable functional programming patterns while maintaining Rust's performance
Iterators + Closures: Functional Programming in Rust
About This Module
This module explores the powerful combination of iterators and closures in Rust, which enables elegant functional programming patterns. You'll learn how to chain iterator methods with closures to create expressive, efficient data processing pipelines. This combination allows you to write concise code for complex operations like filtering, mapping, reducing, and combining data sequences while maintaining Rust's performance guarantees.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
- Chapter 13.2: Processing a Series of Items with Iterators - Focus on iterator methods with closures
- Review Chapter 13.1: Closures for closure capture patterns
- Iterator documentation - Browse common methods like map, filter, fold
Pre-lecture Reflections
Before class, consider these questions:
- How do closures enable powerful iterator chaining patterns that would be difficult with function pointers?
- What are the performance implications of chaining multiple iterator adapters together?
- How does the combination of map and reduce/fold relate to the MapReduce paradigm in distributed computing?
- When would you choose fold vs reduce for aggregation operations?
- How does Rust's type system help prevent common errors in functional programming patterns?
Learning Objectives
By the end of this module, you should be able to:
- Combine iterators with closures for concise data processing
- Use functional programming patterns like map, filter, and fold effectively
- Implement complex algorithms using iterator method chaining
- Choose appropriate aggregation methods (fold, reduce, sum) for different scenarios
- Apply zip to combine multiple data sequences
- Build efficient data processing pipelines using lazy evaluation
Iterator + Closure Magic
- Operate on entire sequence, sometimes lazily by creating a new iterator
- Allows for concise expression of many concepts
for_each applies a function to each element
#![allow(unused)] fn main() { let x = (0..5).for_each(|x| println!("{}",x)); }
filter creates a new iterator that has elements for which the given function is true
#![allow(unused)] fn main() { let not_divisible_by_3 : Vec<_> = (0..10).filter(|x| x % 3 != 0).collect(); println!("{:?}", not_divisible_by_3); }
More Iterator Operations with Closures
- Operate on entire sequence, sometimes lazily by creating a new iterator
- Allows for concise expression of many concepts
map creates a new iterator in which values are processed by a function
struct Fib { current: u128, next: u128, } impl Fib { fn new() -> Fib { Fib{current: 0, next: 1} } } impl Iterator for Fib { type Item = u128; // Calculate the next number in the Fibonacci sequence fn next(&mut self) -> Option<Self::Item> { let now = self.current; self.current = self.next; self.next = now + self.current; Some(now) } } fn main() { let fibonacci_squared : Vec<_> = Fib::new().take(10).map(|x| x*x).collect(); println!("{:?}", fibonacci_squared); }
Calculate Primes with .any()
any is true if the passed function is true on some element
Is a number prime?
fn is_prime(k:u32) -> bool { !(2..k).any(|x| k % x == 0) } fn main() { println!("{}", is_prime(33)); println!("{}", is_prime(31)); }
Create infinite iterator over primes:
#![allow(unused)] fn main() { // create a new iterator let primes = (2..).filter(|k| !(2..*k).any(|x| k % x == 0)); let v : Vec<_> = primes.take(20).collect(); println!("{:?}", v); }
Functional Programming Classic: fold
fold(init, |acc, x| f(acc, x) )-> Initialize expression toinit, execute closure on iterator and accumulate intoacc.
iterator.fold(init, |acc, x|, f(x)) equivalent to
let mut accumulator = init;
while let Some(x) = iterator.next() {
accumulator = f(accumulator,x);
}
println!("{:?}", accumulator);Example: compute
#![allow(unused)] fn main() { let sum_of_squares: i32 = (1..=10).fold(0,|a,x| a + x * x); println!("{}", sum_of_squares); }
#![allow(unused)] fn main() { // Another approach: using `sum` (which can be implemented using `map`) let sum_of_squares: i32 = (1..=10).map(|x| x * x).sum(); println!("{}", sum_of_squares); }
Functional Programming Classic: reduce
reduce(|x, y|, )-> Similar to fold but the initial value is the first element in the iterator
iterator.reduce(f) equivalent to
if let Some(x) = iterator.next() {
let mut accumulator = x;
while let Some(y) = iterator.next() { accumulator = f(accumulator,y}
Some(accumulator)
} else {
None
}Differences from fold:
- no default value for an empty sequence
- output must be the same type as elements of input sequence
- output for length–one sequence equals the only element in the sequence
Example: computing the maximum number in {x^2 mod 7853: x∈[1,...,123]}, i.e. finds the largest squared value (modulo 7853) across all integers from 1 to 123.
#![allow(unused)] fn main() { let x = (1..=123).map(|x| (x*x) % 7853).reduce(|x,y| x.max(y)).unwrap(); println!("{}", x); }
where y is the next element in the iterator.
#![allow(unused)] fn main() { // in this case one can use the builtin `max` method (which can be implemented, using `fold`) let x = (1..=123).map(|x| (x*x) % 7853).max().unwrap(); println!("{}", x); }
Combining Two Iterators: zip
- Returns an iterator of pairs
- The length is the minimum of the lengths
#![allow(unused)] fn main() { let v: Vec<_>= (1..10).zip(11..20).collect(); println!("{:?}", v); }
Inner product of two vectors:
#![allow(unused)] fn main() { let x: Vec<f64> = vec![1.1, 2.2, -1.3, 2.2]; let y: Vec<f64> = vec![2.7, -1.2, -1.1, -3.4]; let inner_product: f64 = x.iter().zip(y.iter()).map(|(a,b)| a * b).sum(); println!("{}", inner_product); }
Recap
for_each- apply function to each elementfilter- create iterator with elements matching a conditionmap- transform elements into new valuesany- test if any element satisfies a conditionfold- accumulate with explicit initial valuereduce- accumulate using first element (returnsOption)zip- combine two iterators into pairs
In-Class Exercise
Time: 5 minutes
Complete the following tasks using iterators and their methods:
-
Create a vector containing the first 10 odd numbers (1, 3, 5, ..., 19)
- Use a range starting from 1
- Use iterator adapters and
collect()
-
Using the Fibonacci iterator from earlier, collect the first 15 Fibonacci numbers into a vector and print them.
-
Create an iterator that:
- Starts with the range 1..=20
- Filters to keep only numbers divisible by 3
- Multiplies each remaining number by 2
- Collects into a vector
Bonus Challenge: Without running the code, predict what this will output:
#![allow(unused)] fn main() { let result: Vec<_> = (0..5).map(|x| x * 2).collect(); println!("{:?}", result); }
Solution Discussion
After attempting the exercise, compare your solutions with a neighbor. Key concepts to verify:
- Did you chain iterator adapters before calling a consumer?
- Did you understand that
mapandfilterreturn iterators, not final values? - Did you remember that iterators are lazy and need a consumer to produce results?
Solutions
Task 1: First 10 odd numbers
#![allow(unused)] fn main() { let odd_numbers: Vec<_> = (1..).step_by(2).take(10).collect(); println!("{:?}", odd_numbers); // Output: [1, 3, 5, 7, 9, 11, 13, 15, 17, 19] }
Alternative solution using filter:
#![allow(unused)] fn main() { let odd_numbers: Vec<_> = (1..20).filter(|x| x % 2 == 1).collect(); println!("{:?}", odd_numbers); }
Task 2: First 15 Fibonacci numbers
struct Fib { current: u128, next: u128, } impl Fib { fn new() -> Fib { Fib{current: 0, next: 1} } } impl Iterator for Fib { type Item = u128; // Calculate the next number in the Fibonacci sequence fn next(&mut self) -> Option<Self::Item> { let now = self.current; self.current = self.next; self.next = now + self.current; Some(now) } } fn main() { let fib_numbers: Vec<_> = Fib::new().take(15).collect(); println!("{:?}", fib_numbers); // Output: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377] }
Task 3: Filter and map
#![allow(unused)] fn main() { let result: Vec<_> = (1..=20) .filter(|x| x % 3 == 0) .map(|x| x * 2) .collect(); println!("{:?}", result); // Output: [6, 12, 18, 24, 30, 36] }
Bonus Challenge
#![allow(unused)] fn main() { let result: Vec<_> = (0..5).map(|x| x * 2).collect(); println!("{:?}", result); // Output: [0, 2, 4, 6, 8] }
Error handling in Rust
About This Module
This module covers error handling in Rust, focusing on the use of the Result enum for recoverable errors and the panic! macro for unrecoverable errors. You'll learn how to propagate errors using the ? operator and how to design functions that can gracefully handle failure scenarios while maintaining Rust's safety and performance guarantees.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 9: Error Handling
- Chapter 9.1: Unrecoverable Errors with panic!
- Chapter 9.2: Recoverable Errors with Result
Pre-lecture Reflections
Before class, consider these questions:
- What are the differences between recoverable and unrecoverable errors in Rust?
- How does the
Resultenum facilitate error handling in Rust? - What are the advantages of using the
?operator for error propagation? - When should you use
panic!versus returning aResult? - How does Rust's approach to error handling compare to exception handling in other languages?
Lecture
Learning Objectives
By the end of this module, you will be able to:
- Understand the difference between recoverable and unrecoverable errors
- Use the
panic!macro for handling unrecoverable errors - Use the
Resultenum for handling recoverable errors - Propagate errors using the
?operator - Design functions that can handle errors gracefully
Error Handling in Rust
Two basic options:
-
terminate when an error occurs: macro
panic!(...) -
pass information about an error: enum
Result<T,E>
Macro panic!(...)
- Use for unrecoverable errors
- Terminates the application
fn divide(a:u32, b:u32) -> u32 { if b == 0 { panic!("I'm sorry, Dave. I'm afraid I can't do that."); } a/b } fn main() { println!("{}", divide(20,7)); //println!("{}", divide(20,0)); // Try uncommenting this line }
Enum Result<T,E>
Provided by the standard library, but shown here for reference.
#![allow(unused)] fn main() { enum Result<T,E> { Ok(T), Err(E), } }
Functions can use it to
- return a result
- or information about an encountered error
fn divide(a:u32, b:u32) -> Result<u32, String> { if b != 0 { Ok(a / b) } else { let str = format!("Division by zero {} {}", a, b); Err(str) } } fn main() { println!("{:?}", divide(20,7)); println!("{:?}", divide(20,0)); }
- Useful when the error best handled somewhere else
- Example: input/output subroutines in the standard library
Common pattern: propagating errors
- We are interested in the positive outcome:
tinOk(t) - But if an error occurs, we want to propagate it
- This can be handled using
matchstatements
fn divide(a:u32, b:u32) -> Result<u32, String> { if b != 0 { Ok(a / b) } else { let str = format!("Division by zero {} {}", a, b); Err(str) } } // compute a/b + c/d fn calculate(a:u32, b:u32, c:u32, d:u32) -> Result<u32, String> { let first = match divide(a,b) { Ok(t) => t, Err(e) => return Err(e), }; let second = match divide(c,d) { Ok(t) => t, Err(e) => return Err(e), }; Ok(first + second) } fn main() { println!("{:?}", calculate(16,4,18,3)); println!("{:?}", calculate(16,0,18,3)); }
The question mark shortcut
-
Place
?after an expression that returnsResult<T,E> -
This will:
- give the content of
Ok(t) - or immediately return the error
Err(e)from the encompassing function
- give the content of
fn divide(a:u32, b:u32) -> Result<u32, String> { if b != 0 { Ok(a / b) } else { let str = format!("Division by zero {} {}", a, b); Err(str) } } // compute a/b + c/d fn calculate(a:u32, b:u32, c:u32, d:u32) -> Result<u32, String> { Ok(divide(a,b)? + divide(c,d)?) } fn main() { println!("{:?}", calculate(16,4,18,3)); println!("{:?}", calculate(16,0,18,3)); }
Optional: try/catch pattern
- In some languages we have the pattern
try/catchorthrow/catchortry/except(C++, Java, Javascript, Python). - Rust does not have something equivalent
The Rust pattern for error handling is the following:
let do_steps = || -> Result<(), MyError> {
do_step_1()?;
do_step_2()?;
do_step_3()?;
Ok(())
};
if let Err(_err) = do_steps() {
println!("Failed to perform necessary steps");
}
- Create a closure with the code you want to guard. Use the ? shorthand inside the closure for anything that can return an Error. Use a match or if let statement to catch the error.
Recap
- Use
panic!for unrecoverable errors - Use
Result<T,E>for recoverable errors - Use
?to propagate errors
Midterm 2 Review
Table of Contents:
- Preliminaries
- 1. Structs and Methods
- 2. Ownership and Borrowing, Strings and Vecs
- 3. Modules, Crates and Projects
- 4. Tests and Error Handling
- 5. Generics and Traits
- 6. Lifetimes
- 7. Closures and Iterators
- Final Tips for the Exam
Suggested way to use this review material
- The material is organized by major topics.
- For each topic, there are:
- links to lecture modules
- high level overview
- examples,
- true/false questions,
- predict the output questions, and
- coding challenges.
- Try to answer the questions without peaking at the solutions.
- The material is not guaranteed to be complete, so you should review the material in the lectures as well as this review material.
Book References:
The lectures modules all start with pre-reading assignments that point to the relevant chapters in The Rust Language Book.
Exam Format:
The exam will be in four parts:
- Part 1 (10 pts): 5 questions, 2 points each -- select all that are true
- Part 2 (16 pts): 4 questions, 4 points each -- find the bug in the code and fix it
- Part 3 (12 pts): 4 questions, 3 points each -- Predict the output and explain why
- Part 4 (12 pts): 2 questions, 6 points each -- hand-coding problems
Total Points: 50
Suggested time budget for each part:
- Part 1: (~10 min)
- Part 2: (~16 min)
- Part 3: (~12 min)
- Part 4: (~22 min)
for a total of 60 minutes and then another 15 minutes to check your work.
Preliminaries
The material for midterm 2 assumes that you have gained proficiency with Rust's basic syntax such as main and function definitions, basic data types including tuples and enums as well as defining and passing values as arguments to functions, etc.
For example you should be familiar enough with Rust syntax type in the following program code from memory, without notes.
Basic main function
// Write a main function that prints "Hello, DS210!"
Expected output:
Hello, DS210!
Basic Function Calling
// Create a function called `print_hello` that takes no arguments and // doesn't return anything, but prints "Hello, DS210!". // Write a main function that calls `print_hello`.
Expected output:
Hello, DS210!
Calling Function with Argument
// Create a function called 'print_hello' that takes an integer argument // and prints, for example for argument `340`, "Hello, DS340!". // Write a main function that call `print_hello with some integer number.
Output for argument 110:
Hello, DS110!
Challenge yourself with increasingly more complex exercises.
If you struggled with remembering the syntax for those exercises, then consider practicing these basics before moving on to the slightly more advanced syntax below. Practice by writing code into an empty Rust Playground.
You can review the basics of Rust syntax in the A1 Midterm 1 Review.
Review basic and complex data types, e.g. tuples, arrays, Vecs, Strings, enums, etc., methods on these data types like len(), push(), pop(), get(), insert(), remove(), etc.
1. Structs and Methods
Modules
Quick Review
Structs group related data together with named fields, providing type safety and semantic meaning. Unlike tuples, fields have names making code self-documenting.
Key Concepts:
- Regular structs:
struct Person { name: String, age: u32 } - Tuple structs:
struct Point3D(f64, f64, f64)- named tuples for type safety - Field access with
.notation - Methods with
self,&self, or&mut self
Examples
#![allow(unused)] fn main() { // Regular struct struct Rectangle { width: u32, height: u32, } // Implementation block with methods impl Rectangle { // Constructor (associated function) fn new(width: u32, height: u32) -> Rectangle { Rectangle { width, height } } // Method borrowing immutably fn area(&self) -> u32 { self.width * self.height } // Method borrowing mutably fn scale(&mut self, factor: u32) { self.width *= factor; self.height *= factor; } } // Tuple struct for type safety struct Miles(f64); struct Kilometers(f64); // Cannot accidentally mix these types! }
True/False Questions
-
T/F: A tuple struct
Point3D(i32, i32, i32)can be assigned to a variable of type(i32, i32, i32). -
T/F: Methods that take
&selfcan modify the struct's fields. -
T/F: You can have multiple
implblocks for the same struct. -
T/F: Struct fields are public by default in Rust.
-
T/F: Associated functions (like constructors) don't take any form of
selfas a parameter.
Answers
- False - Tuple structs create distinct types, even with identical underlying structure
- False -
&selfis immutable; you need&mut selfto modify fields - True - Multiple impl blocks are allowed and sometimes useful
- False - Struct fields are private by default; use
pubto make them public - True - Associated functions are called on the type itself (e.g.,
Rectangle::new())
Predict the Output (3-4 questions)
Question 1:
struct Counter { count: i32, } impl Counter { fn new() -> Counter { Counter { count: 0 } } fn increment(&mut self) { self.count += 1; } } fn main() { let mut c = Counter::new(); c.increment(); c.increment(); println!("{}", c.count); }
Question 2:
struct Point(i32, i32); fn main() { let p = Point(3, 4); println!("{} {}", p.0, p.1); let Point(x, y) = p; println!("{} {}", x, y); }
Question 3:
struct Temperature { celsius: f64, } impl Temperature { fn new(celsius: f64) -> Self { Self { celsius } } fn to_fahrenheit(&self) -> f64 { self.celsius * 1.8 + 32.0 } } fn main() { let temp = Temperature::new(100.0); println!("{:.1}", temp.to_fahrenheit()); }
Question 4:
struct Box3D { width: u32, height: u32, depth: u32, } impl Box3D { fn volume(&self) -> u32 { self.width * self.height * self.depth } } fn main() { let b = Box3D { width: 2, height: 3, depth: 4 }; let v1 = b.volume(); let v2 = b.volume(); println!("{} {}", v1, v2); }
Answers
- Output:
2 - Output:
3 4(newline)3 4 - Output:
212.0 - Output:
24 24
Coding Challenges
Challenge 1: Circle struct
Create a Circle struct with a radius field. Implement methods:
new(radius: f64) -> Circle- constructorarea(&self) -> f64- returns area (use π ≈ 3.14159)scale(&mut self, factor: f64)- multiplies radius by factor
// your code here
Solution
struct Circle { radius: f64, } impl Circle { fn new(radius: f64) -> Circle { Circle { radius } } fn area(&self) -> f64 { 3.14159 * self.radius * self.radius } fn scale(&mut self, factor: f64) { self.radius *= factor; } } fn main() { let mut c = Circle::new(5.0); println!("Area: {}", c.area()); c.scale(2.0); println!("New area: {}", c.area()); }
Challenge 2: Student struct with grade calculation
Create a Student struct with fields for name (String) and three exam scores (exam1, exam2, exam3 as u32). Implement:
new(name: String, e1: u32, e2: u32, e3: u32) -> Studentaverage(&self) -> f64- returns average of three examsletter_grade(&self) -> char- returns 'A' (90+), 'B' (80-89), 'C' (70-79), 'D' (60-69), 'F' (<60)
// your code here
Solution
#![allow(unused)] fn main() { struct Student { name: String, exam1: u32, exam2: u32, exam3: u32, } impl Student { fn new(name: String, e1: u32, e2: u32, e3: u32) -> Student { Student { name, exam1: e1, exam2: e2, exam3: e3 } } fn average(&self) -> f64 { (self.exam1 + self.exam2 + self.exam3) as f64 / 3.0 } fn letter_grade(&self) -> char { let avg = self.average(); if avg >= 90.0 { 'A' } else if avg >= 80.0 { 'B' } else if avg >= 70.0 { 'C' } else if avg >= 60.0 { 'D' } else { 'F' } } } }
2. Ownership and Borrowing, Strings and Vecs
Modules
Quick Review
Ownership Rules:
- Each value has exactly one owner
- When owner goes out of scope, value is dropped
- Ownership can be moved or borrowed
Borrowing:
- Immutable references
&T: multiple allowed, read-only - Mutable references
&mut T: only ONE at a time, exclusive access - References must always be valid (no dangling)
Key Types:
String: heap-allocated, growable, ownedVec<T>: heap-allocated dynamic array, owns elements- Both have ptr, length, capacity on stack
Examples
#![allow(unused)] fn main() { // Ownership transfer (move) let s1 = String::from("hello"); let s2 = s1; // s1 is now invalid // println!("{}", s1); // ERROR! // Borrowing immutably let s3 = String::from("world"); let len = calculate_length(&s3); // borrow println!("{} has length {}", s3, len); // s3 still valid // Borrowing mutably let mut v = vec![1, 2, 3]; add_one(&mut v); // exclusive mutable borrow fn calculate_length(s: &String) -> usize { s.len() } fn add_one(v: &mut Vec<i32>) { for item in v.iter_mut() { *item += 1; } } }
True/False Questions
-
T/F: After
let s2 = s1;wheres1is aString, boths1ands2are valid. -
T/F: You can have multiple immutable references to the same data simultaneously.
-
T/F:
Vec::push()takes&mut selfbecause it modifies the vector. -
T/F: When you pass a
Vec<i32>to a function without&, the function takes ownership. -
T/F: A mutable reference
&mut Tcan coexist with immutable references&Tto the same data. -
T/F:
String::clone()creates a deep copy of the string data on the heap.
Answers
- False - Ownership moves;
s1becomes invalid - True - Multiple immutable borrows are allowed
- True - Modifying requires mutable reference
- True - Without
&, ownership is transferred - False - Cannot have
&mutand&simultaneously - True -
clone()performs a deep copy
Predict the Output
Question 1:
fn main() { let mut v = vec![1, 2, 3]; v.push(4); println!("{}", v.len()); }
Question 2:
fn process(s: String) -> usize { s.len() } fn main() { let text = String::from("hello"); let len = process(text); println!("{}", len); //println!("{}", text); // Would this compile? }
Question 3:
fn main() { let mut s = String::from("hello"); let r1 = &s; let r2 = &s; println!("{} {}", r1, r2); let r3 = &mut s; r3.push_str(" world"); println!("{}", r3); }
Question 4:
fn main() { let v1 = vec![1, 2, 3]; let v2 = v1.clone(); println!("{} {}", v1.len(), v2.len()); }
Answers
- Output:
4 - Output:
5(the second println withtextwould cause compile error - moved) - Output:
hello hello(newline)hello world - Output:
3 3
Coding Challenges
Challenge 1: Fix the borrowing errors
// Fix this code so it compiles fn main() { let mut numbers = vec![1, 2, 3]; let sum = calculate_sum(numbers); double_all(numbers); println!("Sum: {}, Doubled: {:?}", sum, numbers); } fn calculate_sum(v: Vec<i32>) -> i32 { v.iter().sum() } fn double_all(v: Vec<i32>) { for x in v.iter() { x *= 2; } }
Solution
fn main() { let mut numbers = vec![1, 2, 3]; let sum = calculate_sum(&numbers); // borrow instead of move double_all(&mut numbers); // mutable borrow println!("Sum: {}, Doubled: {:?}", sum, numbers); } fn calculate_sum(v: &Vec<i32>) -> i32 { // take reference v.iter().sum() } fn double_all(v: &mut Vec<i32>) { // take mutable reference for x in v.iter_mut() { // mutable iterator *x *= 2; // dereference to modify } }
Challenge 2: String manipulation
Write a function reverse_words(s: &str) -> String that takes a string slice and returns a new String with words in reverse order. For example, "hello world rust" becomes "rust world hello".
hint #1
The string method .split_whitespace() might be very useful.
hint #2
Collect the splitted string into a Vec<&str>.
// Your code here
Solution
fn reverse_words(s: &str) -> String { let words: Vec<&str> = s.split_whitespace().collect(); let mut result = String::new(); for (i, word) in words.iter().rev().enumerate() { if i > 0 { result.push(' '); } result.push_str(word); } result } fn main() { let original = "hello world rust"; let reversed = reverse_words(original); println!("{}", reversed); // "rust world hello" }
3. Modules, Crates and Projects
Modules
Quick Review
Modules organize code within a crate:
modkeyword defines modulespubmakes items publicusebrings items into scope- File structure:
mod.rsormodule_name.rs
Crates and Projects:
- Binary crate: has
main(), produces executable - Library crate: has
lib.rs, provides functionality Cargo.toml: manifest with dependenciescargo build,cargo test,cargo run
Examples
// lib.rs pub mod shapes { pub struct Circle { pub radius: f64, } impl Circle { pub fn new(radius: f64) -> Circle { Circle { radius } } pub fn area(&self) -> f64 { std::f64::consts::PI * self.radius * self.radius } } } // main.rs use crate::shapes::Circle; fn main() { let c = Circle::new(5.0); println!("Area: {}", c.area()); }
True/False Questions
-
T/F: By default, all items (functions, structs, etc.) in a module are public.
-
T/F: A Rust package can have both
lib.rsandmain.rs. -
T/F: The
usestatement imports items at compile time and has no runtime cost. -
T/F: Tests are typically placed in a
testsmodule marked with#[cfg(test)]. -
T/F: External dependencies are listed in
Cargo.tomlunder the[dependencies]section.
Answers
- False - Items are private by default; need
pubfor public access - True - This creates both a library and binary target
- True - Module system is resolved at compile time
- True - This is the standard pattern for unit tests
- True - Dependencies are declared in
Cargo.toml
Predict the Output
Question 1:
mod math { pub fn add(a: i32, b: i32) -> i32 { a + b } fn private_func() { println!("Private"); } } fn main() { println!("{}", math::add(3, 4)); // math::private_func(); // What happens? }
Question 2:
mod outer { pub mod inner { pub fn greet() { println!("Hello from inner"); } } } use outer::inner; fn main() { inner::greet(); }
Answers
- Output:
7(private_func() call would cause compile error - not public) - Output:
Hello from inner
Coding Challenge
Challenge: Create a temperature conversion module
Create a module called temperature with:
- Function
celsius_to_fahrenheit(c: f64) -> f64- fahrenheit = celsius * 1.8 + 32.0
- Function
fahrenheit_to_celsius(f: f64) -> f64- celsius = (fahrenheit - 32.0) / 1.8
- Function
celsius_to_kelvin(c: f64) -> f64- kelvin = celsius + 273.15
All functions should be public.
In a main function, use the module to convert 100°C to Fahrenheit, 32°F to Celsius, and 0°C to Kelvin and print the results.
// your code here
Solution
pub mod temperature { pub fn celsius_to_fahrenheit(c: f64) -> f64 { c * 1.8 + 32.0 } pub fn fahrenheit_to_celsius(f: f64) -> f64 { (f - 32.0) / 1.8 } pub fn celsius_to_kelvin(c: f64) -> f64 { c + 273.15 } } fn main() { use temperature::*; println!("100°C = {}°F", celsius_to_fahrenheit(100.0)); println!("32°F = {}°C", fahrenheit_to_celsius(32.0)); println!("0°C = {}K", celsius_to_kelvin(0.0)); }
4. Tests and Error Handling
Modules
Quick Review
Testing in Rust:
- Unit tests: in same file with
#[cfg(test)]module #[test]attribute marks test functionsassert!,assert_eq!,assert_ne!macroscargo testruns all tests#[should_panic]for testing panicsResult<T, E>return type for tests that can fail
Error Handling in Rust:
See Error Handling for more details.
panic!for unrecoverable errorsResult<T,E>for recoverable errors?to propagate errors
Examples
#![allow(unused)] fn main() { pub fn add(a: i32, b: i32) -> i32 { a + b } #[cfg(test)] mod tests { use super::*; #[test] fn test_add() { assert_eq!(add(2, 3), 5); } #[test] fn test_add_negative() { assert_eq!(add(-1, 1), 0); } #[test] #[should_panic] fn test_overflow() { let _x = i32::MAX + 1; // Should panic in debug mode } } }
True/False Questions
-
T/F: Test functions must return
()orResult<T, E>. -
T/F: The
assert_eq!macro checks if two values are equal using the==operator. -
T/F: Tests marked with
#[should_panic]pass if they panic. -
T/F: Private functions cannot be tested in unit tests.
-
T/F:
cargo testcompiles the code in release mode by default.
Answers
- True - Tests can return these types
- True -
assert_eq!(a, b)checksa == b - True -
#[should_panic]expects the test to panic - False - Unit tests in the same module can access private functions
- False -
cargo testuses debug mode; use--releasefor release mode
Predict the Output
Question 1:
What would the result be for cargo test on this code?
#![allow(unused)] fn main() { #[cfg(test)] mod tests { #[test] fn test_pass() { assert_eq!(2 + 2, 4); } #[test] fn test_fail() { assert_eq!(2 + 2, 5); } } }
Question 2:
What would the result be for cargo test on this code?
fn divide(a: i32, b: i32) -> Result<i32, String> {
if b == 0 {
Err(String::from("Division by zero"))
} else {
Ok(a / b)
}
}
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn test_divide_ok() -> Result<(), String> {
let result = divide(10, 2);
assert_eq!(result, Ok(5));
Ok(())
}
#[test]
fn test_divide_err() {
let result = divide(10, 0);
assert_eq!(result, Err(String::from("Division by zero")));
}
}Answers
- Test passes (10/2 = 5, assertion succeeds, returns Ok(()))
- Test passes (10/0 = error, assertion succeeds, returns Err(String::from("Division by zero")))
Coding Challenge
Challenge: Write tests for a max function
Write a function max_of_three(tup: (i32, i32, i32)) -> i32 that returns the maximum of three integers given in a tuple. Then write at least 3 test cases.
// your code here
Solution
#![allow(unused)] fn main() { pub fn max_of_three(tup: (i32, i32, i32)) -> i32 { if tup.0 >= tup.1 && tup.0 >= tup.2 { tup.0 } else if tup.1 >= tup.2 { tup.1 } else { tup.2 } } #[cfg(test)] mod tests { use super::*; #[test] fn test_first_is_max() { assert_eq!(max_of_three((5, 2, 3)), 5); } #[test] fn test_second_is_max() { assert_eq!(max_of_three((1, 9, 4)), 9); } #[test] fn test_third_is_max() { assert_eq!(max_of_three((2, 3, 10)), 10); } #[test] fn test_all_equal() { assert_eq!(max_of_three((7, 7, 7)), 7); } } }
5. Generics and Traits
Modules
Quick Review
Generics enable code reuse across different types:
- Type parameters:
<T>,<T, U>, etc. - Monomorphization: compiler generates specialized versions
- Zero runtime cost
- Trait bounds constrain generic types:
<T: Display>
Traits define shared behavior:
- Like interfaces in other languages
impl Trait for Typesyntax- Standard traits:
Debug,Clone,PartialEq,PartialOrd,Display, etc. - Trait bounds:
fn foo<T: Trait>(x: T) - Trait bounds can be combined with multiple traits:
fn foo<T: Trait1 + Trait2>(x: T)
Examples
Generic function:
#![allow(unused)] fn main() { // Generic function fn largest<T: PartialOrd>(list: &[T]) -> &T { let mut largest = &list[0]; for item in list { if item > largest { largest = item; } } largest } }
Generic struct:
#![allow(unused)] fn main() { // Generic struct struct Point<T> { x: T, y: T, } impl<T> Point<T> { fn new(x: T, y: T) -> Self { Point { x, y } } } }
Trait definition:
#![allow(unused)] fn main() { // Trait definition trait Summary { fn summarize(&self) -> String; } // Trait implementation struct Article { title: String, author: String, } impl Summary for Article { fn summarize(&self) -> String { format!("{} by {}", self.title, self.author) } } }
True/False Questions
-
T/F: Generics in Rust have runtime overhead because type checking happens at runtime.
-
T/F: A struct
Point<T>where both x and y are type T means x and y must be the same type. -
T/F:
Option<T>andResult<T, E>are examples of generic enums in the standard library. -
T/F: Trait bounds like
<T: Display + Clone>require T to implement both traits. -
T/F: The
deriveattribute can automatically implement certain traits likeDebugandClone.
Answers
- False - Monomorphization happens at compile time; zero runtime cost
- True - Both fields share the same type parameter
- True - Both are generic enums
- True -
+combines multiple trait bounds - True -
#[derive(Debug, Clone)]auto-implements these traits
Predict the Output
Question 1:
fn print_type<T: std::fmt::Display>(x: T) { println!("{}", x); } fn main() { print_type(42); print_type("hello"); print_type(3.14); }
Question 2:
fn swap<T>(a: T, b: T) -> (T, T) { (b, a) } fn main() { let (x, y) = swap(1, 2); println!("{} {}", x, y); }
Question 3:
struct Container<T> { value: T, } impl<T: std::fmt::Display> Container<T> { fn show(&self) { println!("Value: {}", self.value); } } fn main() { let c = Container { value: 42 }; c.show(); }
Question 4:
trait Double { fn double(&self) -> Self; } impl Double for i32 { fn double(&self) -> Self { self * 2 } } fn main() { let x = 5; println!("{}", x.double()); }
Answers
- Output:
42(newline)hello(newline)3.14 - Output:
2 1 - Output:
Value: 42 - Output:
10
Coding Challenges
Challenge 1: Generic pair
Create a generic struct Pair<T> that holds two values of the same type. Implement:
new(first: T, second: T) -> Selfswap(&mut self)- swaps the two valueslarger(&self) -> &T- returns reference to the larger value (requiresT: PartialOrd)
// your code here
Solution
struct Pair<T> { first: T, second: T, } impl<T> Pair<T> { fn new(first: T, second: T) -> Self { Pair { first, second } } fn swap(&mut self) { std::mem::swap(&mut self.first, &mut self.second); } } impl<T: PartialOrd> Pair<T> { fn larger(&self) -> &T { if self.first > self.second { &self.first } else { &self.second } } } fn main() { let mut p = Pair::new(5, 10); println!("{}", p.larger()); // 10 p.swap(); println!("{}", p.larger()); // 10 }
Challenge 2: Trait for area calculation
Define a trait Area with a method area(&self) -> f64. Implement it for Circle (radius) and Rectangle (width, height).
// your code here
Solution
trait Area { fn area(&self) -> f64; } struct Circle { radius: f64, } struct Rectangle { width: f64, height: f64, } impl Area for Circle { fn area(&self) -> f64 { 3.14159 * self.radius * self.radius } } impl Area for Rectangle { fn area(&self) -> f64 { self.width * self.height } } fn main() { let c = Circle { radius: 5.0 }; let r = Rectangle { width: 4.0, height: 6.0 }; println!("Circle area: {}", c.area()); println!("Rectangle area: {}", r.area()); }
6. Lifetimes
Modules
Quick Review
Lifetimes ensure references are valid:
- Prevent dangling references at compile time
- Notation:
'a,'b, etc. - Most lifetimes are inferred
- Explicit annotations needed when ambiguous
- Lifetime elision rules reduce annotations needed
Key Concepts:
- Every reference has a lifetime
- Function signatures sometimes need lifetime annotations
- Structs with references need lifetime parameters
'staticlifetime lasts entire program
Examples
#![allow(unused)] fn main() { // Explicit lifetime annotations fn longest<'a>(x: &'a str, y: &'a str) -> &'a str { if x.len() > y.len() { x } else { y } } // Struct with lifetime struct Book<'a> { title: &'a str, author: &'a str, } // Multiple lifetimes fn first_word<'a, 'b>(s: &'a str, _other: &'b str) -> &'a str { s.split_whitespace().next().unwrap_or("") } // Static lifetime let s: &'static str = "This string lives forever"; }
True/False Questions
-
T/F: All references in Rust have lifetimes, but most are inferred by the compiler.
-
T/F: The lifetime
'staticmeans the reference can live for the entire program duration. -
T/F: Lifetime parameters in function signatures change the actual lifetimes of variables.
-
T/F: A struct that contains references must have lifetime parameters.
-
T/F: The notation
<'a>in a function signature creates a lifetime; it doesn't declare a relationship.
Answers
- True - Lifetime inference works in most cases
- True -
'staticreferences live for the entire program - False - Lifetime annotations describe relationships, don't change actual lifetimes
- True - Structs with references need lifetime parameters
- False -
<'a>declares a lifetime parameter; annotations describe relationships
Predict the Output
Question 1:
fn longest<'a>(x: &'a str, y: &'a str) -> &'a str { if x.len() > y.len() { x } else { y } } fn main() { let s1 = String::from("short"); let s2 = String::from("longer"); let result = longest(&s1, &s2); println!("{}", result); }
Question 2:
fn first<'a>(x: &'a str, _y: &str) -> &'a str { x } fn main() { let s1 = "hello"; let s2 = "world"; println!("{}", first(s1, s2)); }
Answers
- Output:
longer - Output:
hello
Coding Challenge
Challenge: Implement a function with lifetimes
Write a function get_first_sentence<'a>(text: &'a str) -> &'a str that returns the first sentence (up to the first period, or the whole string if no period exists).
// your code here
Solution
fn get_first_sentence<'a>(text: &'a str) -> &'a str { match text.find('.') { Some(pos) => &text[..=pos], None => text, } } fn main() { let text = "Hello world. This is Rust."; let first = get_first_sentence(text); println!("{}", first); // "Hello world." let text2 = "No period here"; let first2 = get_first_sentence(text2); println!("{}", first2); // "No period here" }
7. Closures and Iterators
Modules
Quick Review
Closures are anonymous functions that can capture environment:
- Syntax:
|param| expressionor|param| { body } - Capture variables from surrounding scope
- Enable lazy evaluation
- Used with iterators and functional programming
- A predicate is a closure (or function) that returns a boolean value.
Iterators:
- Trait-based:
Iteratortrait withnext()method - Lazy evaluation - only compute when consumed
- Common methods:
map,filter,fold,collect forloops useIntoIterator- Three forms:
iter(),iter_mut(),into_iter()
Iterator Creation Methods
iter()-> Create an iterator from a collection that yields immutable references(&T)to elementsiter_mut()-> Create an iterator that yields mutable references(&mut T)to elementsinto_iter()-> Consumes the collection and yields owned values(T)transferring ownership to the iterator
Iterator Methods and Adapters
From Iterator Methods and Adapters module:
Pay special attention to what the output is.
into_iter()-> Create an iterator that consumes the collectionnext()-> Get the next element of an iterator (None if there isn't one)enumerate()-> Create an iterator that yields the index and the element (added)collect()-> Put iterator elements in collectiontake(N)-> take first N elements of an iterator and turn them into an iteratorcycle()-> Turn a finite iterator into an infinite one that repeats itselffor_each(||, )-> Apply a closure to each element in the iteratorfilter(||, )-> Create new iterator from old one for elements where closure is truemap(||, )-> Create new iterator by applying closure to input iteratorfilter_map(||, )-> Creates an iterator that both filters and maps (added)any(||, )-> Return true if closure is true for any element of the iteratorfold(a, |a, |, )-> Initialize expression to a, execute closure on iterator and accumulate into areduce(|x, y|, )-> Similar to fold but the initial value is the first element in the iteratorzip(iterator)-> Zip two iterators together to turn them into pairs
Other useful methods:
sum()-> Sum the elements of an iteratorproduct()-> Product the elements of an iteratormin()-> Minimum element of an iteratormax()-> Maximum element of an iteratorcount()-> Count the number of elements in an iteratornth(N)-> Get the Nth element of an iteratorskip(N)-> Skip the first N elements of an iteratorskip_while(||, )-> Skip elements while the closure is true
If the method returns an iterator, you have to do something with the iterator.
See Rust provided methods for the complete list.
Examples
#![allow(unused)] fn main() { // Closure basics let add = |x, y| x + y; let result = add(3, 4); // 7 // Capturing environment let multiplier = 3; let multiply = |x| x * multiplier; println!("{}", multiply(5)); // 15 // Iterators let numbers = vec![1, 2, 3, 4, 5]; // map and filter (lazy) let doubled: Vec<i32> = numbers.iter() .map(|x| x * 2) .filter(|x| x > &5) .copied() .collect(); // fold let sum: i32 = numbers.iter().fold(0, |acc, x| acc + x); // Lazy evaluation let result = Some(5).unwrap_or_else(|| expensive_function()); }
True/False Questions
-
T/F: Closures can capture variables from their environment, but regular functions cannot.
-
T/F: Iterator methods like
mapandfilterare eagerly evaluated. -
T/F: The
collect()method consumes an iterator and produces a collection. -
T/F:
for x in vecmoves ownership, whilefor x in &vecborrows. -
T/F: Closures can have explicit type annotations like
|x: i32| -> i32 { x + 1 }. -
T/F: The
foldmethod requires an initial accumulator value.
Answers
- True - Closures capture environment; functions don't
- False - They're lazy; evaluated only when consumed
- True -
collect()is a consumer that builds a collection - True - Without
&, ownership moves; with&, it borrows - True - Type annotations are optional but allowed
- True -
foldtakes initial value and closure
Predict the Output
Question 1:
fn main() { let numbers = vec![1, 2, 3, 4, 5]; let sum: i32 = numbers.iter().map(|x| x * 2).sum(); println!("{}", sum); }
Question 2:
fn main() { let numbers = vec![1, 2, 3, 4, 5]; let result: Vec<i32> = numbers.iter() .filter(|x| *x % 2 == 0) .map(|x| x * x) .collect(); println!("{:?}", result); }
Question 3:
fn main() { let factor = 3; let multiply = |x| x * factor; println!("{}", multiply(7)); }
Question 4:
fn main() { let numbers = vec![1, 2, 3]; let result = numbers.iter() .fold(0, |acc, x| acc + x); println!("{}", result); }
Answers
- Output:
30(sum of 2, 4, 6, 8, 10) - Output:
[4, 16](squares of even numbers: 2² and 4²) - Output:
21 - Output:
6(1 + 2 + 3)
Coding Challenges
Challenge 1: Custom filter
Write a function count_if<F>(vec: &Vec<i32>, predicate: F) -> usize where F is a closure that takes &i32 and returns bool. The function returns the count of elements satisfying the predicate.
// your code here
Solution
fn count_if<F>(vec: &Vec<i32>, predicate: F) -> usize where F: Fn(&i32) -> bool { let mut count = 0; for item in vec { if predicate(item) { count += 1; } } count } // Alternative using iterators: fn count_if_iter<F>(vec: &Vec<i32>, predicate: F) -> usize where F: Fn(&i32) -> bool { vec.iter().filter(|x| predicate(x)).count() } fn main() { let numbers = vec![1, 2, 3, 4, 5, 6]; let evens = count_if(&numbers, |x| x % 2 == 0); println!("{}", evens); // 3 }
Challenge 2: Iterator chain
Given a Vec<i32>, create an iterator chain that:
- Filters for numbers > 5
- Squares each number
- Sums the results
// your code here
Solution
fn process_numbers(numbers: &Vec<i32>) -> i32 { numbers.iter() .filter(|&&x| x > 5) .map(|x| x * x) .sum() } fn main() { let numbers = vec![1, 3, 6, 8, 10, 2]; let result = process_numbers(&numbers); println!("{}", result); // 6² + 8² + 10² = 36 + 64 + 100 = 200 }
Challenge 3: Custom map
Implement a function apply_to_all<F>(vec: &mut Vec<i32>, f: F) that applies a closure to each element, modifying the vector in place.
// your code here
Solution
fn apply_to_all<F>(vec: &mut Vec<i32>, f: F) where F: Fn(i32) -> i32 { for item in vec.iter_mut() { *item = f(*item); } } fn main() { let mut numbers = vec![1, 2, 3, 4, 5]; apply_to_all(&mut numbers, |x| x * 2); println!("{:?}", numbers); // [2, 4, 6, 8, 10] }
Final Tips for the Exam
- Ownership & Borrowing: Remember the rules - one owner, multiple
&OR one&mut - Lifetimes: Think about what references your function returns and where they come from
- Generics: Use trait bounds when you need specific capabilities (PartialOrd, Display, etc.)
- Iterators: They're lazy - need
collect()orsum()to actually compute - Tests: Write tests that cover normal cases, edge cases, and error cases
- Read error messages: Rust's compiler errors are very helpful - read them carefully!
Good luck on your midterm!
Complexity Analysis: Understanding Algorithm Performance
About This Module
This module covers algorithmic complexity analysis with a focus on how memory is managed in Rust vectors. You'll learn to analyze time and space complexity of operations and understand the performance characteristics of different data structures and algorithms.
Prework
Prework Reading
Please read the following:
- (review) Chapter 8.1: Storing Lists of Values with Vectors
- (optional) Additional reading: Wikipedia: Analysis of Algorithms
Pre-lecture Reflections
- What is the difference between time complexity and space complexity?
- Why is amortized analysis important for dynamic data structures?
- How does Rust's memory management affect algorithm complexity?
Learning Objectives
By the end of this module, you will be able to:
- Analyze time and space complexity using Big O notation
- Understand amortized analysis for vector operations
- Compare complexity of some algorithms and data structures
Complexity Analysis (e.g. memory management in vectors)
Let's dive deeper into algorithmic complexity analysis by considering how memory is manged in Rust Vecs.
Previously: vectors Vec<T>
- Dynamic-length array/list
- Allowed operations:
- access item at specific location
push: add something to the endpop: remove an element from the end
Other languages:
- Python: list
- C++:
vector<T> - Java:
ArrayList<T>/Vector<T>
Implementation details
Challenges
- Size changes: allocate on the heap?
- What to do if a new element added?
- Allocate a larger array and copy everything?
- Linked list?
Solution
- Allocate more space than needed!
- When out of space:
- Increase storage size by, say, 100%
- Copy everything
Under the hood
Variable of type Vec<T> contains:
- pointer to allocated memory
- size: the current number of items
- capacity: how many items could currently fit
Important: size capacity
Example (adding elements to a vector)
Method capacity() reports the current storage size
#![allow(unused)] fn main() { // print out the current size and capacity // define a generic function `info` that takes one argument, `vector`, // of generic `Vec` type and prints it's length and capacity fn info<T>(vector:&Vec<T>) { println!("length = {}, capacity = {}",vector.len(),vector.capacity()); } // Let's keep adding elements to Vec and see what happens to capacity let mut v = Vec::with_capacity(7); // instantiate empty Vec with capacity 7 let mut capacity = v.capacity(); info(&v); for i in 1..=1000 { v.push(i); // push the index onto the Vec // if capacity changed, print the length and new capacity if v.capacity() != capacity { capacity = v.capacity(); info(&v); } }; info(&v); }
Example (decreasing the size of a vector)
#![allow(unused)] fn main() { fn info<T>(vector:&Vec<T>) { println!("length = {}, capacity = {}",vector.len(),vector.capacity()); } // what happens when we decrease the Vec by popping off values? let mut v = vec![10; 1000]; info(&v); // `while let` is a control flow construct that will continue // as long as pattern `Some(_) = v.pop()` matches. // If there is a value to pop, v.pop() returns Option enum, which // is either Some(Vec<T>) // otherwise it will return None and the loop will end. while let Some(_) = v.pop() {} info(&v); }
Questions
- What is happening as we push elements?
- When does it happen?
- How much is it changing by?
- What happens when we pop? Is capacity changing?
Example -- Shrink to Fit
- We can shrink the size of a vector manually
#![allow(unused)] fn main() { fn info<T>(vector:&Vec<T>) { println!("length = {}, capacity = {}",vector.len(),vector.capacity()); } let mut v = vec![10; 1000]; while let Some(_) = v.pop() {} info(&v); for i in 1..=13 { v.push(i); } info(&v); // shrink the size manually v.shrink_to_fit(); info(&v); }
Note: size and capacity not guaranteed to be the same
Example -- Creating a vector with specific capacity
Avoid reallocation if you know how many items to expect.
#![allow(unused)] fn main() { fn info<T>(vector:&Vec<T>) { println!("length = {}, capacity = {}",vector.len(),vector.capacity()); } // creating vector with specific capacity let mut v2 : Vec<i32> = Vec::with_capacity(1234); info(&v2); }
.get() versus .pop()
.get()does not remove from the vector, but you must specify the index.pop()removes the last element from the vector- both return an
Option<T>.get()returnsSome(T)if the index is valid,Noneotherwise.pop()returnsSome(T)if the vector is not empty,Noneotherwise
#![allow(unused)] fn main() { let mut v = Vec::new(); for i in 1..=13 { v.push(i); } println!("{:?}", v); // Does not remove from the vector, but you must specify the index println!("{:?} {:?}", v.get(v.len()-1), v); // But this one does, and removes the last element println!("{:?} {:?}", v.pop(), v); }
Other useful functions
appendAdd vector at the end of anothervec.append(&mut vec2)clearRemove all elements from the vectorvec.clear()dedupRemove consecutive identical elementsvec.dedup(), most useful when combined withsortdrainRemove a slice from the vectorvec.drain(2..4)-- removes and shifts -- expensiveremoveRemove an element from the vectorvec.remove(2)-- removes and shifts -- expensivesortSort the elements of a mutable vectorvec.sort()- Complete list at https://doc.rust-lang.org/std/vec/struct.Vec.html
Sketch of analysis: Amortization
- Inserting an element not constant time (i.e. ) under all conditions
However
-
Assumption: allocating memory size takes either or time
-
Slow operations: current_size time
-
Fast operations: time
What is the average time?
- Consider an initial 100-capacity Vec.
- Continually add element
- First 100 added elements:
- For 101st element:
So on average for the first 101 elements:
- On average: amortized time
- Fast operations pay for slow operations
Dominant terms and constants in notation
We ignore constants and all but dominant terms as :
Which is worse? or ?
Shrinking?
- Can be implemented this way too
- Example: shrink by 50% if less than 25% used
- Most implementations don't shrink automatically
Notations
-> Algorithm takes no more than n time (worst case scenario)
-> Algorithm takes at least n time (best case scenario)
-> Average/Typical running time for the algorithm (average case scenario)
Digression (Sorting Vectors in Rust)
Sorting on on integer vectors works fine.
#![allow(unused)] fn main() { // This works great let mut a = vec![1, 4, 3, 6, 8, 12, 5]; a.sort(); println!("{:?}", a); }
But sorting on floating point vectors does not work directly.
#![allow(unused)] fn main() { // But the compiler does not like this one, since sort depends on total order let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0]; a.sort(); println!("{:?}", a); }
Why?
Because floats in Rust support special values like NaN and inf which don't obey normal sorting rules.
More technically, floats in Rust don't implement the
Ordtrait, only thePartialOrdtrait.The
Ordtrait is a total order, which means that for any two numbers and , either , , or .The
PartialOrdtrait is a partial order, which means that for any two numbers and , either , , , or the comparison is not well defined.
Example -- inf
#![allow(unused)] fn main() { let mut x: f64 = 6.8; println!("{}", x/0.0); }
We can push inf onto a Vec.
#![allow(unused)] fn main() { let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0]; let mut x: f64 = 6.8; a.push(x/0.0); a.push(std::f64::INFINITY); println!("{:?}", a); }
Example -- NaN
#![allow(unused)] fn main() { let mut x: f64 = -1.0; println!("{}", x.sqrt()); }
Similarly, we can push NaN onto a Vec.
#![allow(unused)] fn main() { let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0]; let mut x: f64 = -1.0; a.push(x.sqrt()); a.push(std::f64::NAN); println!("{:?}", a); }
Example -- Sorting with sort_by()
We can work around this by:
- not relying on the Rust implementation of
sort(), but rather - defining our own comparison function using
partial_cmp, which is a required method for the PartialOrd trait, and - using the
.sort_by()function.
#![allow(unused)] fn main() { // This is ok since we don't use sort, sort_by depends on the function you pass in to compute order let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0]; // a.sort(); a.sort_by(|x, y| x.partial_cmp(y).unwrap()); println!("{:?}", a); }
where partial_cmp is a method that returns for types that implement the PartialOrd trait:
Some(std::cmp::Ordering::Equal)when ,Some(std::cmp::Ordering::Less)whenSome(std::cmp::Ordering::Greater)whenNonewhen the comparison is not well defined, e.g x ? NaN
Example -- Can even handle inf
#![allow(unused)] fn main() { let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, std::f32::INFINITY, 6.0, 8.0, 12.0, 5.0]; println!("{:?}", a); a.sort_by(|x, y| x.partial_cmp(y).unwrap()); println!("{:?}", a); }
#![allow(unused)] fn main() { let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, std::f32::INFINITY, 6.0, std::f32::NEG_INFINITY, 8.0, 12.0, 5.0]; println!("{:?}", a); a.sort_by(|x, y| x.partial_cmp(y).unwrap()); println!("{:?}", a); }
#![allow(unused)] fn main() { let mut a: Vec<f32> = vec![1.0, 4.0, 3.0, std::f32::INFINITY, 6.0, 8.0, std::f32::INFINITY, 12.0, 5.0]; println!("{:?}", a); a.sort_by(|x, y| x.partial_cmp(y).unwrap()); println!("{:?}", a); }
Infinity goes to the end:
Infinity has a well-defined ordering in IEEE 754 floating-point arithmetic:
- Positive infinity is explicitly defined as greater than all finite numbers
inf.partial_cmp(finite_number)returnsSome(Ordering::Greater)- This is a valid comparison, so the
unwrap_orfallback is never used - Result: infinity naturally sorts to the end
Just be careful!
It will panic if you try to unwrap a special value like NaN.
#![allow(unused)] fn main() { // When partial order is not well defined in the inputs you get a panic let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0]; let mut x: f32 = -1.0; x = x.sqrt(); a.push(x); println!("{:?}", a); a.sort_by(|x, y| x.partial_cmp(y).unwrap()); println!("{:?}", a); }
Workaround
Return a default value when the comparison is not well defined.
#![allow(unused)] fn main() { // When partial order is not well defined in the inputs you get a panic let mut a = vec![1.0, 4.0, 3.0, 6.0, 8.0, 12.0, 5.0]; // push a NaN (sqrt(-1.0)) let mut x: f32 = -1.0; x = x.sqrt(); a.push(x); // push an inf (10.0/0.0) a.push(10.0/0.0); println!("{:?}", a); a.sort_by(|x, y| x.partial_cmp(y).unwrap_or(std::cmp::Ordering::Less)); println!("{:?}", a); }
NaN goes to the beginning:
The .unwrap_or(std::cmp::Ordering::Less) says: "if the comparison is undefined (returns None), pretend that x is less than y".
So when NaN is compared with any other value:
NaN.partial_cmp(other)→None- Falls back to
Ordering::Less - This means NaN is always treated as "smaller than" everything else
- Result: NaN gets sorted to the beginning
In-Class Piazza Poll
Select all that are true:
-
The
push()operation on a RustVec<T>always has O(1) time complexity in the worst case. -
When a
Vec<T>runs out of capacity and needs to grow, it typically doubles its capacity, resulting in O(n) time for that specific push operation where n is the current size. -
The
pop()operation on a RustVec<T>has O(1) time complexity and automatically shrinks the vector's capacity when the size drops below 25% of capacity. -
The amortized time complexity of
push()operations on aVec<T>is O(1), meaning that averaged over many operations, each push takes constant time. - In Big O notation, O(n² + 100n + 50) simplifies to O(n²) because we ignore constants and non-dominant terms as n approaches infinity.
Solutions
Question 1: FALSE
- The
push()operation is NOT always O(1) in the worst case - When the vector needs to grow (current size equals capacity), it must:
- Allocate new memory (typically double the current capacity)
- Copy all existing elements to the new location
- This copying takes O(n) time where n is the current size
- Only when there's available capacity is push O(1)
Question 2: TRUE
- When a Vec runs out of capacity, it does typically double its capacity
- This resize operation requires allocating new memory and copying all n existing elements
- Therefore, that specific push operation takes O(n) time
- This is why we see capacity jumps in the examples (7 → 14 → 28 → 56, etc.)
Question 3: FALSE
- The
pop()operation does have O(1) time complexity (this part is true) - However,
pop()does NOT automatically shrink the vector's capacity - As shown in the examples, popping all elements leaves the capacity unchanged
- You must explicitly call
shrink_to_fit()to reduce capacity - Most implementations don't shrink automatically to avoid repeated allocate/deallocate cycles
Question 4: TRUE
- Amortized analysis averages the cost over a sequence of operations
- While occasional push operations take O(n) time (during reallocation), most take O(1)
- The expensive operations are infrequent enough that on average, each push is O(1)
- Example: For 101 pushes starting with capacity 100: (100 × 1 + 1 × 100) / 101 ≈ 2, which is still O(1)
Question 5: TRUE
- In Big O notation, we focus on the dominant term as n approaches infinity
- n² grows much faster than n or constant terms
- Therefore: O(n² + 100n + 50) → O(n²)
- We drop the constants (50), the coefficient (100), and the non-dominant term (n)
Hash Maps and Hash Sets: Key-Value Storage
About This Module
This module introduces HashMap and HashSet collections in Rust, which provide efficient key-value storage and set operations. You'll learn how to use these collections for fast lookups, counting, and deduplication tasks common in data processing.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 8.3: Storing Keys with Associated Values in Hash Maps
- (Optional)Additional reading about hash tables and their complexity Wikipedia: Hash table (intro only)
Pre-lecture Reflections -- Part 1
- Why must a
HashMaptake ownership of values likeString, and what memory safety problems does this solve? - How does the
entryAPI help you safely update a value? - The
getmethod returns anOption. Why is this a crucial design choice, and what common bugs does it prevent? - When would you choose to use a
HashMapover aVec, and what is the main performance trade-off for looking up data?
Pre-lecture Reflections -- Part 2
- How do hash maps achieve O(1) average-case lookup time?
- What are the tradeoffs between HashMap and BTreeMap in Rust?
- When would you use a HashSet vs a Vec
for storing unique values? - What makes a good hash function?
Learning Objectives
By the end of this module, you will be able to:
- Create and manipulate HashMap and HashSet collections
- Understand hash table operations and their complexity
- Choose appropriate collection types for different use cases
- Handle hash collisions and understand their implications
Hash maps
Collection HashMap<K,V>
Goal: a mapping from elements of K to elements of V
- elements of
Kcalled keys -- must be unique - elements of
Vcalled values -- need not be unique
Similar structure in other languages:
- Python: dictionaries
- C++:
unordered_map<K,V> - Java:
Hashtable<K,T>
Creating a HashMap
- Create a hash map and insert key-value pairs
- Extract a reference with
.get()
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); // Extracting a reference: returns `Option<&V>` println!("Boston University wins: {:?}", wins.get("Boston University")); println!("MIT wins: {:?}", wins.get("MIT")); }
Inserting a key-value pair if not present
To check if a key is present, and if not, insert a default value, you can use .entry().or_insert().
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); //Insert if not present, you can use `.entry().or_insert()`. wins.entry(String::from("MIT")).or_insert(10); println!("MIT wins: {:?}", wins.get("MIT")); }
Updating a value based on the old value
To update a value based on the old value, you can use .entry().or_insert()
and get a mutable reference to the value.
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); // Updating a value based on the old value: println!("Boston University wins: {:?}", wins.get("Boston University")); { // code block to limit how long the reference lasts let entry = wins.entry(String::from("Boston University")).or_insert(10); *entry += 50; } //wins.insert(String::from("Boston University"),24); println!("Boston University wins: {:?}", wins.get("Boston University")); }
Iterating
You can iterate over each key-value pair with a for loop similar to vectors.
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); for (k,v) in &wins { println!("{}: {}",k,v); }; println!("\nUse .iter(): "); for (k,v) in wins.iter() { println!("{}: {}",k,v); }; }
Iterating and Modifying Values
To modify values, you have to use mutable versions:
#![allow(unused)] fn main() { use std::collections::HashMap; // number of wins in a local Counterstrike league let mut wins = HashMap::<String,u16>::new(); // Insert creates a new key/value if exists and overwrites old value if key exists wins.insert(String::from("Boston University"),24); wins.insert(String::from("Harvard"),22); wins.insert(String::from("Boston College"),20); wins.insert(String::from("Northeastern"),32); for (k,v) in &wins { println!("{}: {}",k,v); }; println!("\nUse implicit mutable iterator: "); for (k,v) in &mut wins { *v += 1; println!("{}: {}",k,v); }; println!("\nUse .iter_mut(): "); for (k,v) in wins.iter_mut() { *v += 1; println!("{}: {}",k,v); }; }
Using HashMaps with Match statements
- Let's use a hash map to store the price of different items in a cafe
#![allow(unused)] fn main() { use std::collections::HashMap; let mut crispy_crêpes_café = HashMap::new(); crispy_crêpes_café.insert(String::from("Nutella Crêpe"),5.85); crispy_crêpes_café.insert(String::from("Strawberries and Nutella Crêpe"),8.75); crispy_crêpes_café.insert(String::from("Roma Tomato, Pesto and Spinach Crêpe"),8.90); crispy_crêpes_café.insert(String::from("Three Mushroom Crêpe"),8.90); fn on_the_menu(cafe: &HashMap<String,f64>, s:String) { print!("{}: ",s); match cafe.get(&s) { // .get() returns an Option enum None => println!("not on the menu"), Some(price) => println!("${:.2}",price), } } on_the_menu(&crispy_crêpes_café, String::from("Four Mushroom Crêpe")); on_the_menu(&crispy_crêpes_café, String::from("Three Mushroom Crêpe")); }
Summary of Useful HashMap Methods
Basic Operations:
new(): Creates an empty HashMap.insert(key, value): Adds a key-value pair to the map. Returns true if the key was not present, false otherwise.remove(key): Removes a key-value pair from the map. Returns true if the key was present, false otherwise.get(key): Returns a reference to the value in the map, if any, that is equal to the given key.contains_key(key): Checks if the map contains a specific key. Returns true if present, false otherwise.len(): Returns the number of key-value pairs in the map.is_empty(): Checks if the map contains no key-value pairs.clear(): Removes all key-value pairs from the map.drain(): Returns an iterator that removes all key-value pairs and yields them. The map becomes empty after this operation.
Iterators and Views:
iter(): Returns an immutable iterator over the key-value pairs in the map.iter_mut(): Returns a mutable iterator over the key-value pairs in the map.keys(): Returns an iterator over the keys in the map.values(): Returns an iterator over the values in the map.values_mut(): Returns a mutable iterator over the values in the map.
See the documentation for more details.
How Hash Tables Work
Internal Representation
Array of Option
- A hash map is represented as an array of buckets, e.g. capacity
- The array is an array of
Option<T>enums likeVec<Option<T>>) , - And the
Some(<T>)variant has valueTwith tuple(key, value, hash) - So the internal representation is like
Vec<Option<(K, V, u64)>>
Hash function
- Use a hash function which is like a pseudorandom number generator with key as the seed, e.g.
- Pseudorandom means that the same key will always produce the same hash, but different keys will produce different hashes.
- Then take modulo of capacity , e.g.
index = hash % 8 = 6 - So ultimately maps keys into one of the buckets
Hash Function Examples
Let's calculate hash and index for different inputs using Rust's built-in hash function.
use std::collections::hash_map::DefaultHasher; use std::hash::{Hash, Hasher}; fn hash_function(input: &str) -> u64 { let mut hasher = DefaultHasher::new(); input.hash(&mut hasher); hasher.finish() } fn main() { let B = 8; // capacity of the hash map (e.g. number of buckets) let input = "Hello!"; let hash = hash_function(input); let index = hash % B; println!("Hash of '{}' is: {} and index is: {}", input, hash, index); let input = "Hello"; // slight change in input let hash = hash_function(input); let index = hash % B; println!("Hash of '{}' is: {} and index is: {}", input, hash, index); let input = "hello"; // slight change in input let hash = hash_function(input); let index = hash % B; println!("Hash of '{}' is: {} and index is: {}", input, hash, index); }
- Any collisions?
- Try increasing the capacity to 16 and see how the index changes.
More Hash Function Examples
- Keys don't have to be strings.
- They can be any type that implements the
Hashtrait.
use std::collections::hash_map::DefaultHasher; use std::hash::{Hash, Hasher}; fn generic_hash_function<T: Hash>(input: &T) -> u64 { let mut hasher = DefaultHasher::new(); input.hash(&mut hasher); hasher.finish() } fn main() { // Using the generic hash function with different types println!("\nUsing generic_hash_function:"); println!("String hash: {}", generic_hash_function(&"Hello, world!")); println!("Integer hash: {}", generic_hash_function(&42)); // println!("Float hash: {}", generic_hash_function(&3.14)); // what if we try float? println!("Bool hash: {}", generic_hash_function(&true)); println!("Tuple hash: {}", generic_hash_function(&(1, 2, 3))); println!("Vector hash: {}", generic_hash_function(&vec![1, 2, 3, 4, 5])); println!("Char hash: {}", generic_hash_function(&'A')); }
What if you try to hash a float?
General ideas
- Store keys (and associated values and hashes) in buckets
- Indexing: Use hash function to find bucket holding key and value.
Collision: two keys mapped to the same bucket
- Very unlikely given the pseudorandom nature of the hash function
- What to do if two keys in the same bucket
Handling collisions
Probing
- Each bucket entry: (key, value, hash)
- Use a deterministic algorithm to find an open bucket
Inserting:
- entry busy: try , , etc.
- insert into first empty
Searching:
- try , , , etc.
- stop when found or empty entry
Handling collisions, example
Step 1
Step 1: Empty hash map with 4 buckets
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | | empty | | empty |
+-------+ +-------+ +-------+ +-------+
Step 2
Step 2: Insert key="apple", hash("apple") = 42
hash("apple") = 42
42 % 4 = 2 ← insert at index 2
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | |apple,v| | empty |
| | | | | h=42 | | |
+-------+ +-------+ +-------+ +-------+
^
insert here
Step 3
Step 3: Insert key="banana", hash("banana") = 14
hash("banana") = 14
14 % 4 = 2 ← collision! index 2 is occupied, and not same key
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | |apple,v| | empty |
| | | | | h=42 | | |
+-------+ +-------+ +-------+ +-------+
^
occupied, check next
Step 4
Step 4: Linear probing - check next bucket (index 3)
Index 2 is full, try (2+1) % 4 = 3
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
| empty | | empty | |apple,v| |banana,v|
| | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
insert here
Step 5
Step 5: Insert key="cherry", hash("cherry") = 10
hash("cherry") = 10
10 % 4 = 2 ← collision again!
Check index 2: occupied (apple), not (cherry)
Check index 3: occupied (banana), not (cherry)
Check index 0: empty! ← wrap around and insert
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
insert here after wrapping around
Searching for a key
Current state of hash map:
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
Step 1
Step 1: Search for key="cherry"
hash("cherry") = 10
10 % 4 = 2 ← start searching at index 2
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
check here first
Step 2
Step 2: Check index 2
Index 2: key = "apple" ≠ "cherry"
bucket occupied, continue probing
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
not found, try next
Step 3
Step 3: Check index 3 (next probe)
Index 3: key = "banana" ≠ "cherry"
bucket occupied, continue probing
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
not found, try next
Step 4
Step 4: Check index 0 (wrap around)
Index 0: key = "cherry" = "cherry" ✓
FOUND! Return value
Index: 0 1 2 3
+-------+ +-------+ +-------+ +-------+
|cherry,v| | empty | |apple,v| |banana,v|
| h=10 | | | | h=42 | | h=14 |
+-------+ +-------+ +-------+ +-------+
^
FOUND: return value v
Key point: Linear probing continues until we either:
- Find a matching key (success)
- Find an empty bucket (key doesn't exist)
- Check all buckets (hash map is full)
What is worse case scenario?
-
All keys map to the same bucket.
-
We have to check all buckets to find the key.
-
This is time complexity.
-
This is the worst case scenario for linear probing.
What is the average case scenario?
-
Each bucket has 1 key.
-
We have to check about 1 bucket to find the key.
-
This is time complexity.
-
This is the average case scenario for linear probing.
Growing the collection: amortization
Keep track of the number of filled entries.
When the number of keys
- Double
- Pick new hash function
- Move the information
Adversarial data
-
Could create lots of collisions
-
Potential basis for denial of service attacks
What makes a good hash function?
- Uniform distribution of inputs to the buckets available!!!
- Consistent hashing adds the property that not too many things move around when the number of buckets changes
http://www.partow.net/programming/hashfunctions/index.html
https://en.wikipedia.org/wiki/Consistent_hashing
https://doc.rust-lang.org/std/collections/struct.HashMap.html
To Dig Deeper (Optional)
Clone, inspect and debug/single-step through a simple implementation that supports creation, insert, get and remove.
See how index is found from hashing the key.
See how collision is handled.
Hashing with custom types in Rust
How do we use custom datatypes as keys?
Required for hashing:
- check if
Kequal - compute a hash function for elements of
K
#![allow(unused)] fn main() { use std::collections::HashMap; struct Point { x:i64, y:i64, } let point = Point{x:2,y:-1}; let mut elevation = HashMap::new(); elevation.insert(point,2.3); }
Most importantly:
[E0277] Error: the trait bound `Point: Eq` is not satisfied
[E0277] Error: the trait bound `Point: Hash` is not satisfied
Required traits for custom types
In order for a data structure to work as a key for hashmap, they need three traits:
PartialEq(required byEq)- ✅ Symmetry: If a == b, then b == a.
- ✅ Transitivity: If a == b and b == c, then a == c.
- ❌ Reflexivity is NOT guaranteed (because e.g. NaN != NaN in floats).
Eq- ✅ Reflexivity: a == a is always true.
- ✅ Symmetry: If a == b, then b == a.
- ✅ Transitivity: If a == b and b == c, then a == c.
Hash- Supports deterministic output of a hash function
- Consistency with Equality -- if two values are equal , then their hashes are equal
- Non-Invertibility -- One way. You cannot reconstruct the original value from the hash
- etc...
Default implementation
EqandPartialEqare automatically derived for most types.
#![allow(unused)] fn main() { use std::collections::HashMap; #[derive(Debug,Hash,Eq,PartialEq)] struct DistanceKM(u64); let mut tired = HashMap::new(); tired.insert(DistanceKM(30),true); println!("{:?}", tired); }
Reminder: All the traits that you can automatically derive from
- Clone: Allow user to make an explicit copy
- Copy: Allow user to make an implicit copy
- Debug: Allow user to print contents
- Default: Allow user to initialize with default values (Default::default())
- Hash: Allow user to use it as a key to a hash map or set.
- Eq: Allow user to test for equality
- Ord: Allow user to sort and fully order types
- PartialEq: Obeys most rules for equality but not all
- PartialOrd: Obeys most rules for ordering but not all
Using Floats as Keys
Note: You can use this for HW7.
Use ordered_float crate to get a type that implements Eq and Hash.
A wrapper around floats providing implementations of Eq, Ord, and Hash.
NaN is sorted as greater than all other values and equal to itself, in contradiction with the IEEE standard.
use ordered_float::OrderedFloat;
use std::f32::NAN;
use std::collections::{HashMap, HashSet};
fn main() {
let mut v = [OrderedFloat(NAN), OrderedFloat(2.0), OrderedFloat(1.0)];
v.sort();
assert_eq!(v, [OrderedFloat(1.0), OrderedFloat(2.0), OrderedFloat(NAN)]);
let mut m: HashMap<OrderedFloat<f32>, String> = HashMap::new();
m.insert(OrderedFloat(3.14159), "pi".to_string());
assert!(m.contains_key(&OrderedFloat(3.14159)));
let mut s: HashSet<OrderedFloat<f32>> = HashSet::new();
s.insert(OrderedFloat(3.14159));
assert!(s.contains(&OrderedFloat(3.14159)));Using Floats as Keys (Alternative)
Not all basic types support the Eq and Hash traits (f32 and f64 do not). The reasons have to do with the NaN and Infinity problems we discussed last time.
- If you find yourself needing floats as keys consider converting the float to a collection of integers
- Floating point representation consists of Sign, Exponent and Mantissa, each integer
float_num = (-1)^sign * mantissa * 2^exponent where
signis -1 or 1mantissaisu23between 0 and 2^23exponentisi8between -127 and 128
// Built-in Rust library for traits on numbers
cargo add num-traits
#![allow(unused)] fn main() { let num:f64 = 3.14159; // Some float println!("num: {:32.21}", num); }
Question: Why is the number printed different than the number assigned?
Answer: Floating point can't exactly represent every decimal number. See above.
Let's decompose the floating point number into its components:
use num_traits::Float;
let num:f64 = 3.14159; // Some float
println!("num: {:32.21}", num);
let base:f64 = 2.0;
// Deconstruct the floating point
let (mantissa, exponent, sign) = Float::integer_decode(num);
println!("mantissa: {} exponent: {} sign: {}", mantissa, exponent, sign);
// Conver to f64
let sign_f:f64 = sign as f64;
let mantissa_f:f64 = mantissa as f64;
let exponent_f:f64 = base.powf(exponent as f64);
// Recalculate the floating point value
let new_num:f64 = sign_f * mantissa_f * exponent_f;
println!("{:32.31} {:32.31}", num, new_num);mantissa: 7074231776675438 exponent: -51 sign: 1
3.1415899999999998826183400524314 3.1415899999999998826183400524314
Let's check it:
#![allow(unused)] fn main() { let mantissa:u64 = 7074231776675438; let exponent:i8 = -51; let sign:i8 = 1; let base:f64 = 2.0; //convert to f64 let sign_f:f64 = sign as f64; let mantissa_f:f64 = mantissa as f64; let exponent_f:f64 = base.powf(exponent as f64); // Recalculate the floating point value let new_num:f64 = sign_f * mantissa_f * exponent_f; println!("{:32.31}", new_num); }
HashSet<K>
"A HashMap without values"
- No value associated with keys
- Just a set of items
- Same implementation
- Fastest way to do membership tests and some set operations
Creating a HashSet
- Create:
HashSet::new() .insert(),.is_empty(),.contains()
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); println!("Is empty: {}", covid.is_empty()); // insert values for i in 2019..=2022 { covid.insert(i); }; println!("Is empty: {}", covid.is_empty()); println!("Contains 2019: {}", covid.contains(&2019)); println!("Contains 2015: {}", covid.contains(&2015)); }
Growing the collection: amortization
- Let's monitor the length and capacity as we insert values.
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); println!("Length: {}, Capacity: {}", covid.len(), covid.capacity()); println!("Is empty: {}", covid.is_empty()); // insert values for i in 2019..=2022 { covid.insert(i); println!("Length: {}, Capacity: {}", covid.len(), covid.capacity()); }; println!("Length: {}, Capacity: {}", covid.len(), covid.capacity()); println!("Is empty: {}", covid.is_empty()); }
- More expensive than growing a
Vecbecause we need to rehash all the elements.
Iterating over a HashSet
You can iterate over a HashSet with a for loop.
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); // insert values for i in 2019..=2022 { covid.insert(i); }; // use the implicit iterator for year in &covid { print!("{} ",year); } println!(); // use the explicit iterator for year in covid.iter() { print!("{} ",year); } println!(); }
Question: Why aren't the years in the order we inserted them?
Using .get() and .insert()
We can use .get() and .insert(), similarly to how we used them in HashMaps.
#![allow(unused)] fn main() { use std::collections::HashSet; // create let mut covid = HashSet::new(); // insert values for i in 2019..=2022 { covid.insert(i); }; // Returns `None` if not in the HashSet println!("{:?}", covid.get(&2015)); println!("{:?}", covid.get(&2021)); covid.insert(2015); // insert 2015 if not present covid.insert(2020); // insert 2020 if not present // iterate over the set for year in &covid { print!("{} ",year); } }
Summary of Useful HashSet Methods
Basic Operations:
new(): Creates an empty HashSet.insert(value): Adds a value to the set. Returns true if the value was not present, false otherwise.remove(value): Removes a value from the set. Returns true if the value was present, false otherwise.contains(value): Checks if the set contains a specific value. Returns true if present, false otherwise.len(): Returns the number of elements in the set.is_empty(): Checks if the set contains no elements.clear(): Removes all elements from the set.drain(): Returns an iterator that removes all elements and yields them. The set becomes empty after this operation.
Set Operations:
union(&self, other: &HashSet<T>): Returns an iterator over the elements that are in self or other (or both).intersection(&self, other: &HashSet<T>): Returns an iterator over the elements that are in both self and other.difference(&self, other: &HashSet<T>): Returns an iterator over the elements that are in self but not in other.symmetric_difference(&self, other: &HashSet<T>): Returns an iterator over the elements that are in self or other, but not in both.is_subset(&self, other: &HashSet<T>): Checks if self is a subset of other.is_superset(&self, other: &HashSet<T>): Checks if self is a superset of other.is_disjoint(&self, other: &HashSet<T>): Checks if self has no elements in common with other.
Iterators and Views:
iter(): Returns an immutable iterator over the elements in the set.get(value): Returns a reference to the value in the set, if any, that is equal to the given value.
See the documentation for more details.
In-Class Exercise 1: Word Frequency Counter
Task: Create a HashMap that counts the frequency of each word in the following sentence:
"rust is awesome rust is fast rust is safe"Your code should:
- Split the sentence into words. (Hint: Use
.split_whitespace()on your string and iterate over the result.) - Count how many times each word appears using a HashMap
- Print each word and its frequency
Hint: Use .entry().or_insert() to initialize or increment counts.
Expected Output:
rust: 3
is: 3
awesome: 1
fast: 1
safe: 1
Solution
use std::collections::HashMap; fn main() { let sentence = "rust is awesome rust is fast rust is safe"; let mut word_count = HashMap::new(); for word in sentence.split_whitespace() { let count = word_count.entry(word).or_insert(0); *count += 1; } for (word, count) in &word_count { println!("{}: {}", word, count); } }
In-Class Exercise 2: Programming Languages Analysis
Task: Two developers list their known programming languages. Create two HashSets and perform set operations to analyze their skills.
Developer 1 knows: Rust, Python, JavaScript, C++, Go
Developer 2 knows: Python, Java, JavaScript, Ruby, Go
Your code should find and print:
- Languages both developers know (intersection)
- Languages unique to Developer 1 (difference)
- All languages known by at least one developer (union)
- Languages known by exactly one developer (symmetric difference)
Hint: Create two HashSets and use set operations methods shown earlier.
Solutions will be added here after class.
Solution
use std::collections::HashSet; fn main() { // Insert one at a time let mut dev1 = HashSet::new(); dev1.insert("Rust"); dev1.insert("Python"); dev1.insert("JavaScript"); dev1.insert("C++"); dev1.insert("Go"); // Iterate over a vector and insert let mut dev2 = HashSet::new(); let dev2_languages = vec!["Python", "Java", "JavaScript", "Ruby", "Go"]; for lang in dev2_languages { dev2.insert(lang); } println!("Languages both know:"); for lang in dev1.intersection(&dev2) { println!(" {}", lang); } println!("\nLanguages unique to Developer 1:"); for lang in dev1.difference(&dev2) { println!(" {}", lang); } println!("\nAll languages known:"); for lang in dev1.union(&dev2) { println!(" {}", lang); } println!("\nLanguages known by exactly one:"); for lang in dev1.symmetric_difference(&dev2) { println!(" {}", lang); } }
Linked Lists in Rust
About This Module
This module explores linked list data structures in Rust, covering both the theoretical concepts and practical implementation challenges. Students will learn about different types of linked lists (singly and doubly linked), understand their computational complexity, and discover why implementing linked lists in Rust requires careful consideration of ownership rules. The module compares various implementation approaches and discusses when to use linked lists versus other data structures.
Prework
Before this lecture, please read:
- The Rust Book Chapter 15.1: "Using Box
to Point to Data on the Heap" - https://doc.rust-lang.org/book/ch15-01-box.html - The Rust Book Chapter 15.2: "Treating Smart Pointers Like Regular References with Deref" - https://doc.rust-lang.org/book/ch15-02-deref.html
- Learning Rust With Entirely Too Many Linked Lists - https://rust-unofficial.github.io/too-many-lists/ (Introduction and Chapter 1)
Pre-lecture Reflections
- Why can't you implement a recursive data structure directly in Rust without using
Box<T>? - What are the memory layout differences between arrays and linked lists?
- How do ownership rules affect pointer-based data structures in Rust?
Learning Objectives
By the end of this lecture, you should be able to:
- Understand the structure and operations of linked lists
- Analyze the computational complexity of linked list operations
- Implement basic linked lists in Rust using
Box<T>and proper ownership patterns - Compare the performance characteristics of different linked list variants
- Choose appropriate data structures based on access patterns and performance requirements
What is a linked list?
- A recursive data structure
- Simplest version is a single pointer (head) that points to the first element in the list
- Each list element contains some data and a pointer to the next element in the list
- A special pointer value (None) used to indicate the end of the list
- If first == None then the list is empty
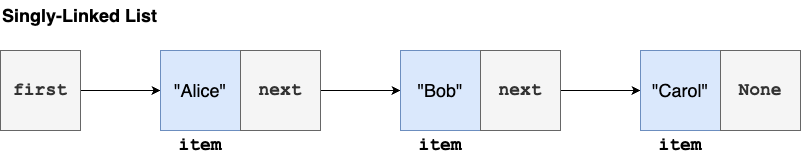
Inserting and Removing from the beginning of the list
Assume you have a new list element "John". How do you add it to the list?
"John".next = first
first = "John"
How about getting an element out of the list?
item = first
first = item.next
item.next = NULL
return item
Common optimization for lists
- Doubly linked list
- Tail pointer
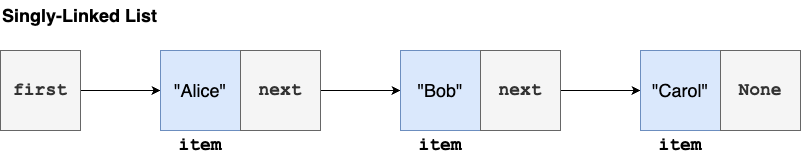

Cost of list operations
- Insert to Front: (SLL O(1), DLL O(1))
- Remove from Front (SLL O(1), DLL O(1))
- Insert to Back (SLL O(N), DLL O(1))
- Remove from Back (SLL O(N), DLL O(1))
- Insert to Middle (SLL O(N), DLL O(N))
- Remove from Middle (SLL O(N), DLL O(N))
Rust's LinkedList
#![allow(unused)] fn main() { use std::collections::LinkedList; let mut list = LinkedList::from([1, 2, 3]); println!("{:?}", list); list.push_front(0); println!("{:?}", list); list.push_back(4); println!("{:?}", list); list.pop_front(); println!("{:?}", list); list.pop_back(); println!("{:?}", list); }
Summary of Useful LinkedList Methods
push_front(value): Adds a value to the front of the list.push_back(value): Adds a value to the back of the list.pop_front(): Removes and returns the value from the front of the list.pop_back(): Removes and returns the value from the back of the list.front(): Returns a reference to the value at the front of the list.back(): Returns a reference to the value at the back of the list.len(): Returns the number of elements in the list.is_empty(): Returns true if the list is empty, false otherwise.clear(): Removes all elements from the list.drain(): Returns an iterator that removes all elements and yields them. The list becomes empty after this operation.
See the documentation for more details.
Don't use LinkedList!
Warning from the Rust documentation on LinkedList:
NOTE: It is almost always better to use Vec or VecDeque because array-based containers are generally faster, more memory efficient, and make better use of CPU cache.
We'll see VecDeque in a later lecture.
Moving on...
Recap
- Linked lists are a recursive data structure
- They are not contiguous in memory, and poor processor cache utilization
- Simple to access the beginning or end
Stack Data Structure in Rust
About This Module
This module introduces the stack data structure, a fundamental Last-In-First-Out (LIFO) container. Students will learn about stack operations, computational complexity, and multiple implementation strategies using both linked lists and vectors. The module explores the trade-offs between different implementations and demonstrates practical applications of stacks in programming and data science.
Prework
Before this lecture, please read:
- (Review) The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
- (Review) Rust std::collections documentation - https://doc.rust-lang.org/std/collections/index.html
Pre-lecture Reflections
- What are some real-world examples where LIFO behavior is useful?
- How might stack implementation affect performance in different scenarios?
- What are the memory layout differences between stack implementations using vectors vs. linked lists?
Learning Objectives
By the end of this lecture, you should be able to:
- Understand the LIFO principle and stack operations
- Implement stacks using different underlying data structures
- Analyze the computational complexity of stack operations
- Compare performance characteristics of vector-based vs. linked list-based stacks
- Choose appropriate stack implementations based on use case requirements
Stacks
- A Stack is a container of objects that are inserted and removed according the LIFO (Last In First Out) principle
- Insertions are known as "Push" operations while removals are known as "Pop" operations
Universal Stack Operations
Stack operations would be along the lines of:
- push(object): Insert object onto top of stack. Input: object, Output: none
- pop(): Remove top object from stack and return it. Input: none, Output: object
- size(): Number of objects in stack
- isEmpty(): Return boolean indicated if stack is empty
- top() or peek(): Return a reference to top object in the stack without removing it
Question: Which Rust data structure could we use to implement a stack?
Computational complexity of Stack operations
Assume we are using a singly (or doubly) linked list
- Push: O(1)
- Pop: O(1)
- Size: O(1) (keep an auxiliary counter)
- isEmpty: O(1)
- top: O(1)
Using Vectors to implement a stack
- Implementing a stack using a vector is straightforward.
- We can build on
Vec<T>methods.
#![allow(unused)] fn main() { #[derive(Debug)] pub struct Stack<T> { v: Vec<T>, } impl <T> Stack<T> { pub fn new() -> Self { Stack {v : Vec::new() } } pub fn push(&mut self, obj:T) { self.v.push(obj) } pub fn pop(&mut self) -> Option<T> { return self.v.pop(); } pub fn size(&mut self) -> usize { return self.v.len(); } pub fn isEmpty(&mut self) -> bool { return self.v.len() == 0; } pub fn top(&mut self) -> Option<&T> { return self.v.last() } } }
Using our stack implementation
Now let's use it!
#[derive(Debug)] pub struct Stack<T> { v: Vec<T>, } impl <T> Stack<T> { pub fn new() -> Self { Stack {v : Vec::new() } } pub fn push(&mut self, obj:T) { self.v.push(obj) } pub fn pop(&mut self) -> Option<T> { return self.v.pop(); } pub fn size(&mut self) -> usize { return self.v.len(); } pub fn isEmpty(&mut self) -> bool { return self.v.len() == 0; } pub fn top(&mut self) -> Option<&T> { return self.v.last() } } fn main() { let mut s: Stack<i32> = Stack::new(); println!("Pushing 13, 11, and 9\n"); s.push(13); s.push(11); s.push(9); println!("size: {}", s.size()); println!("isEmpty: {}", s.isEmpty()); println!("\ntop: {:?}", s.top()); println!("pop: {:?}", s.pop()); println!("size: {}", s.size()); println!("\ntop: {:?}", s.top()); println!("pop: {:?}", s.pop()); println!("size: {}", s.size()); println!("\ntop: {:?}", s.top()); println!("pop: {:?}", s.pop()); println!("size: {}", s.size()); println!("isEmpty: {}", s.isEmpty()); println!("\ntop: {:?}", s.top()); println!("pop: {:?}", s.pop()); }
Which implementation is better: LinkedList or Vec?
- Computation complexity is the same for both (at least on average)
- The Vector implementation has the occasional long operation which may be undesirable in a real-time system
BUT the most important consideration is spatial locality of reference.
- In a vector objects will be contiguous in memory so accessing one will fetch its neighbors into the cache for faster access
- In the linked list version each object is allocated independently so their placement in memory is unclear
In-Class Poll
True or False:
-
In a stack, the most recently added element is the first one to be removed.
- True ✓ (This is the definition of LIFO - Last In First Out)
-
The pop() operation on a stack has O(n) time complexity when using a singly linked list implementation.
- False ✗ (pop() is O(1) for both linked list and vector implementations)
-
A vector-based stack implementation may occasionally have long operations due to resizing.
- True ✓ (When the vector needs to grow, it must allocate new memory and copy elements)
-
The top() or peek() operation removes the top element from the stack.
- False ✗ (top/peek only returns a reference without removing the element; pop removes it)
-
Vector-based stacks generally have better spatial locality of reference than linked list-based stacks.
- True ✓ (Vector elements are contiguous in memory, improving cache performance)
Recap
- Stacks are a fundamental data structure
- They are implemented using a vector or a linked list
- They are a Last-In-First-Out (LIFO) data structure
Queue Data Structure in Rust
About This Module
This module explores queue data structures, which follow the First-In-First-Out (FIFO) principle. Students will learn about queue operations, various implementation strategies, and the trade-offs between different approaches. The module covers both custom implementations and Rust's standard library VecDeque, with a focus on performance considerations and practical applications in data processing and algorithms.
Prework
Before this lecture, please read:
- The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
- Rust std::collections::VecDeque documentation - https://doc.rust-lang.org/std/collections/struct.VecDeque.html
- The Rust Book Chapter 4: "Understanding Ownership" - https://doc.rust-lang.org/book/ch04-00-understanding-ownership.html (review for clone operations)
Pre-lecture Reflections
- What are some real-world scenarios where FIFO ordering is essential?
- Why might using a
Vecwithremove(0)be problematic for queue operations? - How does memory layout affect performance in different queue implementations?
Learning Objectives
By the end of this lecture, you should be able to:
- Understand the FIFO principle and queue operations
- Implement queues using different underlying data structures
- Analyze performance trade-offs between queue implementations
- Use Rust's
VecDequeeffectively for both stack and queue operations - Choose appropriate data structures based on access patterns and performance requirements
Queues

Queue:
- FIFO: first in first out
- add items at the end
- get items from the front
Question: Why is it problematic to use Vec as a Queue?
Generic Queue operations
Warning: This is not Rust syntax.
- enqueue(object): Insert object at the end of the queue. Input: object, Output: none
- dequeue(): Remove an object from the front of the queue and return it. Input: none, Output: object
- size(): Number of objects in queue
- isEmpty(): Return boolean indicated if queue is empty
- front(): Return a reference to front object in the queue without removing it
Queue Complexity using Singly Linked List?
- Remember in a singly linked list the most recent element is first pointer while the oldest is at the tail end of the list
- Adding a queue element O(1)
- Removing a queue element requires list traversal so O(n)
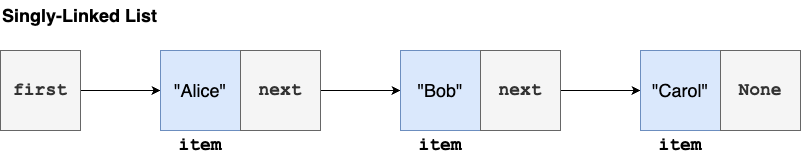
You can do better with doubly linked lists and tail pointer
Assume first points to most recently added element and last to oldest element
- Adding a queue element still O(1)
- Removing the older element O(1)
- But the memory fragmentation issues persist

The VecDeque container in Rust
- generalization of queue and stack
- accessing front: methods
push_front(x)andpop_front() - accessing back: methods
push_back(x)andpop_back() pop_frontandpop_backreturnOption<T>
Using VecDeque as a Stack
Use push_back and pop_back
#![allow(unused)] fn main() { use std::collections::VecDeque; // using as a stack: push_back & pop_back let mut stack = VecDeque::new(); stack.push_back(1); stack.push_back(2); stack.push_back(3); println!("{:?}",stack.pop_back()); println!("{:?}",stack.pop_back()); stack.push_back(4); stack.push_back(5); println!("{:?}",stack.pop_back()); }
Using VecDeque as a Queue
#![allow(unused)] fn main() { use std::collections::VecDeque; // using as a queue: push_back & pop_front let mut queue = VecDeque::new(); queue.push_back(1); queue.push_back(2); queue.push_back(3); println!("{:?}",queue.pop_front()); println!("{:?}",queue.pop_front()); queue.push_back(4); queue.push_back(5); println!("{:?}",queue.pop_front()); }
VecDeque operation semantics
- push_back + pop_back (Stack Behavior)
- push_front + pop_front (Stack Behavior)
- push_back + pop_front (Queue Behavior)
- push_front + pop_back (Queue Behavior)
Implementation of VecDeque
- use an array allocated on the heap (think of it as a circular buffer)
- keep index of the front and end
- wrap around
Out of space?
- double the size
- good complexity due to amortization
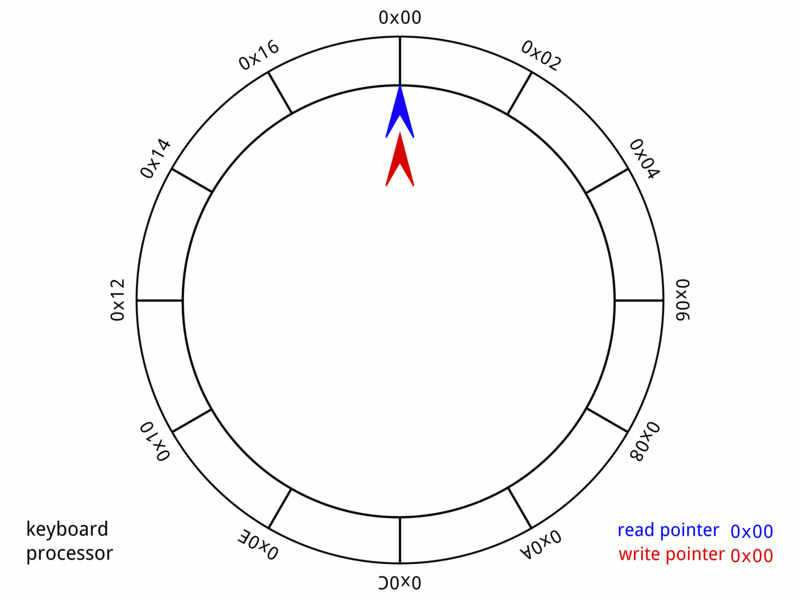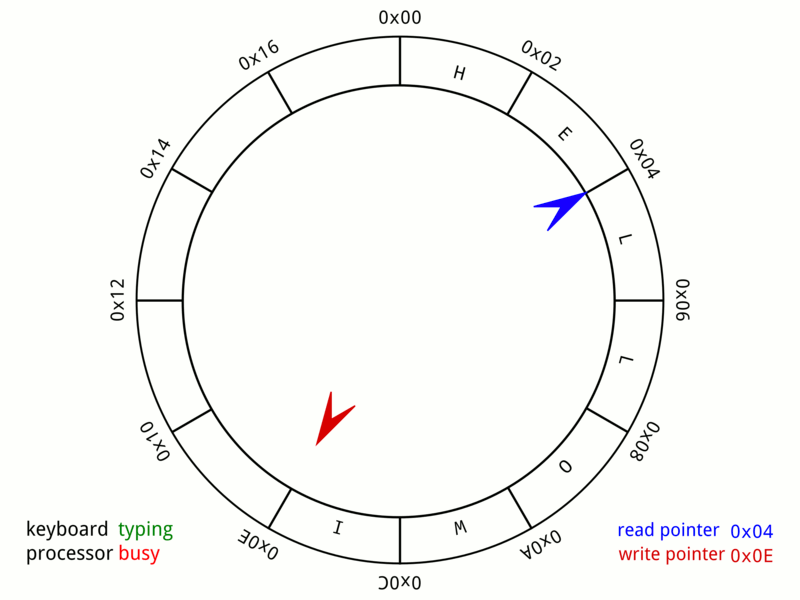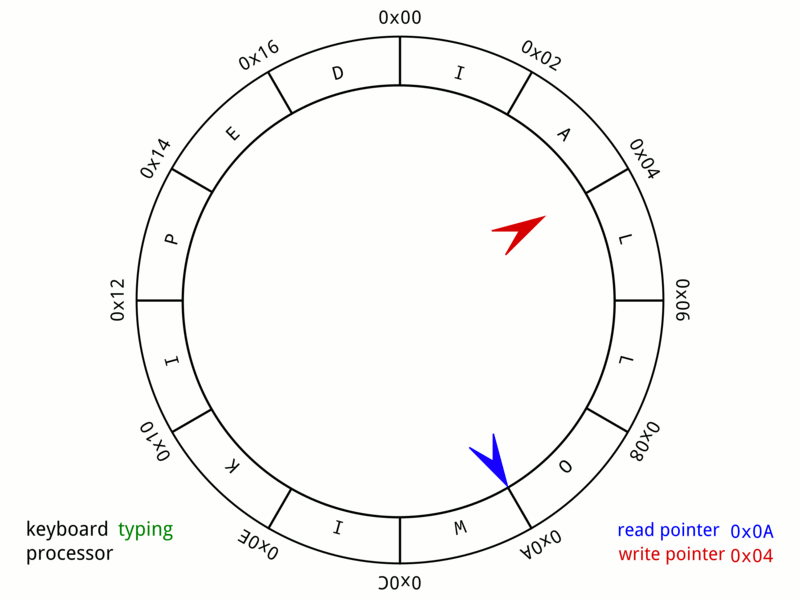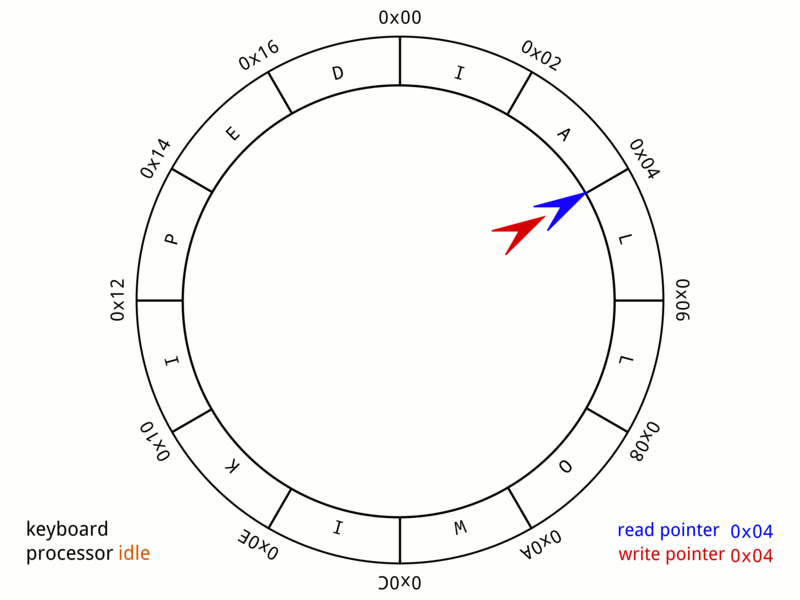
See Wikipedia: Circular Buffer for more details.
Priority Queues (for a later lecture)

In-Class Poll
True or False:
-
In a queue data structure, the first element added is the first element removed (FIFO principle).
- True ✓ (This is the definition of FIFO - First In First Out)
-
When using a singly linked list to implement a queue, both enqueue and dequeue operations can be performed in O(1) time complexity.
- False ✗ (enqueue is O(1) and dequeue is O(n) for singly linked list)
-
Rust's
VecDequecan function as both a stack and a queue depending on which methods you use.- True ✓ (VecDeque can be used as both stack and queue depending on the methods used)
-
To use a
VecDequeas a queue, you should usepush_back()to add elements andpop_back()to remove elements.- False ✗ (To use as a queue, you should use
push_back()to add elements andpop_front()to remove elements)
- False ✗ (To use as a queue, you should use
-
VecDequeis implemented using a doubly linked list that grows by 1 as needed.- False ✗ (VecDeque is implemented using a circular buffer)
Recap
Collections Deep Dive: Entry API, BTreeMap, and Circular Buffers
About This Module
This module provides a deep dive into advanced collection patterns essential for HW7. You'll master the Entry API for efficient HashMap/BTreeMap updates, learn BTreeMap for ordered data with range queries, use the ordered-float crate for float keys, and implement circular buffers with VecDeque.
Prework
Prework Reading
Please read the following:
- The Rust Book: HashMap - Review Entry API section
- BTreeMap Documentation
- VecDeque Documentation
- ordered-float crate
Pre-lecture Reflections
- What's the difference between using
.get()then.insert()vs using the Entry API? - When would you want keys to be sorted (BTreeMap) vs unsorted (HashMap)?
- Why can't
f64be used directly as a HashMap/BTreeMap key? - What's the difference between a regular queue and a circular buffer?
Learning Objectives
By the end of this module, you will be able to:
- Use the Entry API to efficiently update collections without double lookups
- Choose between HashMap and BTreeMap based on requirements
- Use BTreeMap for ordered data, range queries, and percentile calculations
- Work with float keys using the ordered-float crate
- Implement circular buffers with VecDeque for rolling window calculations
Part 1: Mastering the Entry API
The Double-Lookup Problem
A common pattern when updating HashMaps:
#![allow(unused)] fn main() { use std::collections::HashMap; fn count_words_inefficient(text: &str) -> HashMap<String, usize> { let mut counts = HashMap::new(); for word in text.split_whitespace() { // DON'T: This does TWO lookups! if counts.contains_key(word) { let count = counts.get_mut(word).unwrap(); *count += 1; } else { counts.insert(word.to_string(), 1); } } counts } let result = count_words_inefficient("rust is awesome rust is fast"); println!("{:?}", result); }
Problem: We look up the key twice - once to check, once to modify.
The Entry API Solution
#![allow(unused)] fn main() { use std::collections::HashMap; fn count_words_efficient(text: &str) -> HashMap<String, usize> { let mut counts = HashMap::new(); for word in text.split_whitespace() { // DO: Single lookup with Entry API! *counts.entry(word.to_string()).or_insert(0) += 1; } counts } let result = count_words_efficient("rust is awesome rust is fast"); println!("{:?}", result); }
Understanding Entry
The .entry() method returns an Entry enum:
#![allow(unused)] fn main() { use std::collections::HashMap; let mut map: HashMap<&str, i32> = HashMap::new(); println!("{:?}", map.entry("key")); // Entry can be Occupied or Vacant match map.entry("key") { std::collections::hash_map::Entry::Occupied(entry) => { println!("Key exists with value: {}", entry.get()); } std::collections::hash_map::Entry::Vacant(entry) => { println!("Key doesn't exist, inserting..."); entry.insert(42); } } println!("{:?}", map.entry("key")); }
Entry API Methods
or_insert: Insert default if vacant, return mutable referenceor_insert_with: Insert computed value if vacant (lazy evaluation)or_default: Insert Default::default() if vacant, e.g. 0 for i32, "" for String, etc. (types with Default trait)and_modify: Modify existing value, or insert default
#![allow(unused)] fn main() { use std::collections::HashMap; let mut scores: HashMap<String, Vec<i32>> = HashMap::new(); // or_insert: Insert default if vacant, return mutable reference scores.entry("Alice".to_string()).or_insert(vec![]).push(95); scores.entry("Alice".to_string()).or_insert(vec![]).push(87); // or_insert_with: Insert computed value if vacant (lazy evaluation) scores.entry("Bob".to_string()).or_insert_with(|| { println!("Computing default for Bob..."); vec![100] // This only runs if key is vacant }); // or_default: Insert Default::default() if vacant let mut counts: HashMap<String, usize> = HashMap::new(); *counts.entry("hello".to_string()).or_default() += 1; // and_modify: Modify existing value, or insert default counts.entry("hello".to_string()) .and_modify(|c| *c += 1) .or_insert(1); println!("Scores: {:?}", scores); println!("Counts: {:?}", counts); }
Entry API for Grouping (Split-Apply-Combine)
Perfect for grouping data by categories:
#![allow(unused)] fn main() { use std::collections::HashMap; let data = vec![("A", 10), ("B", 20), ("A", 30), ("B", 40), ("A", 50)]; // Group values by category let mut groups: HashMap<&str, Vec<i32>> = HashMap::new(); for (category, value) in data { groups.entry(category).or_default().push(value); } // Now calculate aggregates per group for (category, values) in &groups { let sum: i32 = values.iter().sum(); let mean = sum as f64 / values.len() as f64; println!("{}: values={:?}, sum={}, mean={:.1}", category, values, sum, mean); } }
HW7 Connection: This pattern is the foundation of
GroupedSeriesin Part 2!
Entry API Works with BTreeMap Too!
#![allow(unused)] fn main() { use std::collections::BTreeMap; let mut sorted_counts: BTreeMap<String, usize> = BTreeMap::new(); for word in "rust is awesome rust is fast".split_whitespace() { *sorted_counts.entry(word.to_string()).or_insert(0) += 1; } // BTreeMap iterates in sorted key order! for (word, count) in &sorted_counts { println!("{}: {}", word, count); } }
Part 2: BTreeMap for Ordered Data
HashMap vs BTreeMap
| Feature | HashMap | BTreeMap |
|---|---|---|
| Lookup | O(1) average | O(log n) |
| Iteration order | Random | Sorted by key |
| Range queries | ❌ Not supported | ✅ Supported |
| Key requirement | Hash + Eq | Ord |
| Memory | Less predictable | More predictable |
When to Use BTreeMap
Use BTreeMap when you need:
- Sorted iteration over keys
- Range queries (get all keys between X and Y)
- Min/max key operations
- Percentile calculations
- Keys that don't implement
Hash
Note: See modules on graphs, trees, and binary search trees for background.
BTreeMap: Sorted Iteration
#![allow(unused)] fn main() { use std::collections::BTreeMap; let mut temps: BTreeMap<u32, f64> = BTreeMap::new(); temps.insert(2020, 14.9); temps.insert(2018, 14.7); temps.insert(2022, 15.1); temps.insert(2019, 14.8); temps.insert(2021, 15.0); // Iteration is always in sorted order by key! println!("Global temperatures by year:"); for (year, temp) in &temps { println!(" {}: {:.1}°C", year, temp); } // First and last entries println!("\nFirst: {:?}", temps.first_key_value()); println!("Last: {:?}", temps.last_key_value()); }
Note the order of years inserted and the order from the iteration.
BTreeMap: Range Queries
One of BTreeMap's killer features:
#![allow(unused)] fn main() { use std::collections::BTreeMap; use std::ops::Bound; let mut events: BTreeMap<u64, String> = BTreeMap::new(); events.insert(100, "Login".to_string()); events.insert(150, "View page".to_string()); events.insert(200, "Click button".to_string()); events.insert(250, "Submit form".to_string()); events.insert(300, "Logout".to_string()); // Get events in time range [150, 250] println!("Events from 150-250:"); for (time, event) in events.range(150..=250) { println!(" t={}: {}", time, event); } // Events before time 200 println!("\nEvents before 200:"); for (time, event) in events.range(..200) { println!(" t={}: {}", time, event); } // Using Bound for more control use std::ops::Bound::{Included, Excluded}; println!("\nEvents in (150, 300):"); for (time, event) in events.range((Excluded(150), Excluded(300))) { println!(" t={}: {}", time, event); } }
BTreeMap for Histogram Bins
Perfect for building sorted histograms:
#![allow(unused)] fn main() { use std::collections::BTreeMap; fn build_histogram(data: &[f64], bin_width: f64) -> BTreeMap<i64, usize> { let mut bins: BTreeMap<i64, usize> = BTreeMap::new(); for &value in data { // Calculate bin index (floor division) let bin = (value / bin_width).floor() as i64; *bins.entry(bin).or_insert(0) += 1; } bins } let data = vec![1.2, 2.5, 2.7, 3.1, 3.8, 4.2, 4.5, 5.0, 5.5]; let hist = build_histogram(&data, 1.0); println!("Histogram (bin_width=1.0):"); for (bin, count) in &hist { let start = *bin as f64; let end = start + 1.0; let bar = "*".repeat(*count); println!(" [{:.1}, {:.1}): {} {}", start, end, bar, count); } }
HW7 Connection: This is essentially what
Histogramin Part 3 does!
Part 3: Using Floats as Keys with ordered-float
The Problem with Float Keys
use std::collections::BTreeMap;
// This WON'T compile!
let mut map: BTreeMap<f64, String> = BTreeMap::new();
map.insert(3.14, "pi".to_string());
// Error: the trait bound `f64: Ord` is not satisfiedWhy? Floats have NaN (Not a Number) which breaks ordering:
NaN != NaN(violates reflexivity)NaNis not less than, equal to, or greater than any value
Solution: ordered-float Crate
Add to Cargo.toml:
[dependencies]
ordered-float = "4.2"
Then use OrderedFloat:
use ordered_float::OrderedFloat;
use std::collections::BTreeMap;
fn main() {
let mut map: BTreeMap<OrderedFloat<f64>, String> = BTreeMap::new();
// Wrap floats in OrderedFloat
map.insert(OrderedFloat(3.14), "pi".to_string());
map.insert(OrderedFloat(2.72), "e".to_string());
map.insert(OrderedFloat(1.41), "sqrt(2)".to_string());
// Iteration is sorted by float value!
for (key, value) in &map {
println!("{:.2}: {}", key.0, value);
}
// Access the inner value with .0
let pi_key = OrderedFloat(3.14);
println!("\nLookup {}: {:?}", pi_key.0, map.get(&pi_key));
}OrderedFloat for Histogram Bins
use ordered_float::OrderedFloat;
use std::collections::BTreeMap;
struct Histogram {
bins: BTreeMap<OrderedFloat<f64>, usize>,
bin_width: f64,
}
impl Histogram {
fn new(bin_width: f64) -> Self {
Histogram {
bins: BTreeMap::new(),
bin_width,
}
}
fn add(&mut self, value: f64) {
let bin_edge = (value / self.bin_width).floor() * self.bin_width;
*self.bins.entry(OrderedFloat(bin_edge)).or_insert(0) += 1;
}
fn get_count(&self, value: f64) -> usize {
let bin_edge = (value / self.bin_width).floor() * self.bin_width;
self.bins.get(&OrderedFloat(bin_edge)).copied().unwrap_or(0)
}
fn cumulative_distribution(&self) -> Vec<(f64, f64)> {
let total: usize = self.bins.values().sum();
let mut cumulative = 0;
self.bins.iter()
.map(|(bin_edge, &count)| {
cumulative += count;
(bin_edge.0 + self.bin_width / 2.0, cumulative as f64 / total as f64)
})
.collect()
}
}HW7 Connection: This is exactly how
Histogramin Part 3 is structured!
Part 4: VecDeque for Circular Buffers
What is a Circular Buffer?
A circular buffer (ring buffer) is a fixed-size data structure that:
- Overwrites oldest data when full
- Perfect for "sliding window" or "rolling" calculations
- Efficient O(1) operations at both ends
Initial (capacity 4):
[_, _, _, _] (empty)
After push 1, 2, 3:
[1, 2, 3, _]
After push 4:
[1, 2, 3, 4] (full)
After push 5 (overwrites oldest):
[5, 2, 3, 4] → conceptually [2, 3, 4, 5]
VecDeque Review
#![allow(unused)] fn main() { use std::collections::VecDeque; let mut deque: VecDeque<i32> = VecDeque::new(); // Add to back (queue behavior) deque.push_back(1); deque.push_back(2); deque.push_back(3); println!("Deque: {:?}", deque); // [1, 2, 3] // Remove from front let first = deque.pop_front(); println!("Popped: {:?}", first); // Some(1) println!("Deque: {:?}", deque); // [2, 3] // Also supports push_front and pop_back deque.push_front(0); println!("Deque: {:?}", deque); // [0, 2, 3] }
Implementing a Rolling Buffer
#![allow(unused)] fn main() { use std::collections::VecDeque; struct RollingBuffer { buffer: VecDeque<f64>, capacity: usize, } impl RollingBuffer { fn new(capacity: usize) -> Self { RollingBuffer { buffer: VecDeque::with_capacity(capacity), capacity, } } fn push(&mut self, value: f64) { if self.buffer.len() == self.capacity { self.buffer.pop_front(); // Remove oldest } self.buffer.push_back(value); // Add newest } fn mean(&self) -> Option<f64> { if self.buffer.is_empty() { None } else { let sum: f64 = self.buffer.iter().sum(); Some(sum / self.buffer.len() as f64) } } fn is_full(&self) -> bool { self.buffer.len() == self.capacity } } // Example: Rolling average of last 3 values let mut rolling = RollingBuffer::new(3); for value in [10.0, 20.0, 30.0, 40.0, 50.0] { rolling.push(value); println!("After {}: mean = {:?}, full = {}", value, rolling.mean(), rolling.is_full()); } }
Rolling Statistics Applications
#![allow(unused)] fn main() { use std::collections::VecDeque; struct RollingStats { buffer: VecDeque<f64>, capacity: usize, } impl RollingStats { fn new(capacity: usize) -> Self { RollingStats { buffer: VecDeque::with_capacity(capacity), capacity, } } fn push(&mut self, value: f64) { if self.buffer.len() == self.capacity { self.buffer.pop_front(); } self.buffer.push_back(value); } fn mean(&self) -> Option<f64> { if self.buffer.is_empty() { return None; } let sum: f64 = self.buffer.iter().sum(); Some(sum / self.buffer.len() as f64) } fn std_dev(&self) -> Option<f64> { if self.buffer.len() < 2 { return None; } let mean = self.mean()?; let variance: f64 = self.buffer.iter() .map(|&x| (x - mean).powi(2)) .sum::<f64>() / (self.buffer.len() - 1) as f64; Some(variance.sqrt()) } } // Detect anomalies using rolling statistics let data = [100.0, 102.0, 98.0, 101.0, 150.0, 99.0, 103.0]; let mut stats = RollingStats::new(4); for &value in &data { stats.push(value); if let (Some(mean), Some(std)) = (stats.mean(), stats.std_dev()) { let z_score = (value - mean).abs() / std; if z_score > 2.0 { println!("ANOMALY: {} (z-score: {:.2})", value, z_score); } else { println!("Normal: {} (mean: {:.1}, std: {:.1})", value, mean, std); } } } }
HW7 Connection: This is the
RollingBufferyou'll implement in Part 3!
Summary: Collections for HW7
| HW7 Part | Collections Used | Key Patterns |
|---|---|---|
| Part 1 | HashMap, HashSet | Entry API for counting, set operations |
| Part 2 | HashMap | Entry API for grouping, split-apply-combine |
| Part 3 | BTreeMap, VecDeque | OrderedFloat for keys, circular buffer |
Key Takeaways
- Entry API eliminates double lookups - use it everywhere!
- BTreeMap when you need sorted keys or range queries
- ordered-float enables float keys in ordered collections
- VecDeque is perfect for fixed-size sliding windows
In-Class Exercise: Rolling Window Statistics
Task: Implement a function that computes a rolling mean over a data stream.
Given a stream of temperature readings and a window size, output the rolling mean after each reading.
Use Rust Playground or VSCode to develop your solution.
fn rolling_mean(data: &[f64], window_size: usize) -> Vec<f64> {
// TODO: Implement using VecDeque
todo!()
}
// Test it
let data = vec![20.0, 22.0, 21.0, 23.0, 25.0, 24.0];
let means = rolling_mean(&data, 3);
for (i, (val, mean)) in data.iter().zip(means.iter()).enumerate() {
println!("Step {}: value={}, rolling_mean={:.1}", i, val, mean);
}
// Output:
// Step 0: value=20, rolling_mean=20.0 (window: [20])
// Step 1: value=22, rolling_mean=21.0 (window: [20, 22])
// Step 2: value=21, rolling_mean=21.0 (window: [20, 22, 21])
// Step 3: value=23, rolling_mean=22.0 (window: [22, 21, 23])
// Step 4: value=25, rolling_mean=23.0 (window: [21, 23, 25])
// Step 5: value=24, rolling_mean=24.0 (window: [23, 25, 24])Bonus: Add detection of values more than 2 standard deviations from the rolling mean.
Solution
#![allow(unused)] fn main() { use std::collections::VecDeque; fn rolling_mean(data: &[f64], window_size: usize) -> Vec<f64> { let mut buffer: VecDeque<f64> = VecDeque::with_capacity(window_size); let mut results = Vec::new(); for &value in data { // If buffer is full, remove oldest value if buffer.len() == window_size { buffer.pop_front(); } // Add new value buffer.push_back(value); // Calculate mean of current window let sum: f64 = buffer.iter().sum(); let mean = sum / buffer.len() as f64; results.push(mean); } results } // Test it let data = vec![20.0, 22.0, 21.0, 23.0, 25.0, 24.0]; let means = rolling_mean(&data, 3); for (i, (val, mean)) in data.iter().zip(means.iter()).enumerate() { println!("Step {}: value={}, rolling_mean={:.1}", i, val, mean); } // Output: // Step 0: value=20, rolling_mean=20.0 (window: [20]) // Step 1: value=22, rolling_mean=21.0 (window: [20, 22]) // Step 2: value=21, rolling_mean=21.0 (window: [20, 22, 21]) // Step 3: value=23, rolling_mean=22.0 (window: [22, 21, 23]) // Step 4: value=25, rolling_mean=23.0 (window: [21, 23, 25]) // Step 5: value=24, rolling_mean=24.0 (window: [23, 25, 24]) }
Bonus Solution (with anomaly detection):
#![allow(unused)] fn main() { use std::collections::VecDeque; fn rolling_mean_with_anomaly(data: &[f64], window_size: usize) -> Vec<(f64, bool)> { let mut buffer: VecDeque<f64> = VecDeque::with_capacity(window_size); let mut results = Vec::new(); for &value in data { // Check for anomaly BEFORE adding to buffer (compare to previous window) let is_anomaly = if buffer.len() >= 2 { let mean: f64 = buffer.iter().sum::<f64>() / buffer.len() as f64; let variance: f64 = buffer.iter() .map(|&x| (x - mean).powi(2)) .sum::<f64>() / (buffer.len() - 1) as f64; let std_dev = variance.sqrt(); // Z-score > 2 means anomaly std_dev > 0.0 && (value - mean).abs() / std_dev > 2.0 } else { false }; // Update buffer if buffer.len() == window_size { buffer.pop_front(); } buffer.push_back(value); // Calculate current mean let mean = buffer.iter().sum::<f64>() / buffer.len() as f64; results.push((mean, is_anomaly)); } results } // Test with an anomaly let data = vec![20.0, 21.0, 20.0, 22.0, 50.0, 21.0]; // 50.0 is anomaly let results = rolling_mean_with_anomaly(&data, 4); for (i, (val, (mean, anomaly))) in data.iter().zip(results.iter()).enumerate() { let flag = if *anomaly { " ⚠️ ANOMALY!" } else { "" }; println!("value={}: mean={:.1}{}", val, mean, flag); } }
Key insights:
- VecDeque gives O(1) push_back and pop_front operations
- The window naturally "slides" by removing oldest and adding newest
- For anomaly detection, compare the new value against the previous window's statistics
Next Lecture Preview
In the next lecture, we'll cover:
- Quantile and percentile calculations
- Graph representation and traversal (BFS, DFS)
- Algorithm design patterns
Algorithms for Data Science: Quantiles, Graphs, and Algorithm Design
About This Module
This module covers essential algorithms for data science applications. You'll learn quantile calculations for statistical analysis, graph representation and traversal algorithms (BFS/DFS), and algorithm design patterns including split-apply-combine, greedy algorithms, and divide-and-conquer approaches.
Prework
Prework Reading
Please read the following:
- Wikipedia: Percentile - Focus on calculation methods
- Wikipedia: Breadth-first search
- Wikipedia: Depth-first search
Pre-lecture Reflections
- What's the difference between percentile and quantile?
- Why might BFS find the shortest path in an unweighted graph?
- When would you use DFS vs BFS for graph exploration?
- What is the "greedy" approach to solving problems?
Learning Objectives
By the end of this module, you will be able to:
- Calculate quantiles and percentiles using linear interpolation
- Understand interquartile range (IQR) and its uses
- Implement ranking algorithms (standard and dense rank)
- Represent graphs using adjacency lists
- Implement BFS and DFS traversals
- Apply algorithm design patterns to data problems
Part 1: Quantiles and Statistical Algorithms
What are Quantiles?
Quantiles divide sorted data into equal parts:
- Quartiles (4 parts): Q1 (25%), Q2/median (50%), Q3 (75%)
- Percentiles (100 parts): P50 = median, P95 = 95th percentile
- Deciles (10 parts): D1 (10%), D5 (50%), etc.
Sorted data: [1, 2, 3, 4, 5, 6, 7, 8, 9]
Q1 Q2 Q3
↓ ↓ ↓
[1, 2, 3, 4, 5, 6, 7, 8, 9]
25% 50% 75%
Calculating Quantiles: Linear Interpolation
For quantile q (0.0 to 1.0) on sorted data of length n:
position = q * (n - 1)
lower_idx = floor(position)
upper_idx = ceil(position)
fraction = position - lower_idx
if lower_idx == upper_idx:
result = data[lower_idx]
else:
result = data[lower_idx] * (1 - fraction) +
data[upper_idx] * fraction
Quantile Implementation
fn quantile(data: &[f64], q: f64) -> Option<f64> { if data.is_empty() || !(0.0..=1.0).contains(&q) { return None; } // Sort the data let mut sorted = data.to_vec(); sorted.sort_by(|a, b| a.partial_cmp(b).unwrap()); // Calculate position let pos = q * (sorted.len() - 1) as f64; let lower = pos.floor() as usize; let upper = pos.ceil() as usize; //println!("For q: {}, index position is: {}, lower is: {}, upper is: {}", q, pos, lower, upper); //println!("lower f[{}]: {}, upper f[{}]: {}", lower, sorted[lower], upper, sorted[upper]); if lower == upper { Some(sorted[lower]) } else { // Linear interpolation let fraction = pos - lower as f64; Some(sorted[lower] * (1.0 - fraction) + sorted[upper] * fraction) } } fn main() { let data = vec![1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0]; //let data = vec![-1.0, 2.0, 4.4, 6.7, 11.2, 22.8, 83.1, 124.7]; println!("Q1 (25%): {:?}", quantile(&data, 0.25)); // 2.5 println!("Q2 (50%): {:?}", quantile(&data, 0.50)); // 5.0 println!("Q3 (75%): {:?}", quantile(&data, 0.75)); // 7.5 println!("P90: {:?}", quantile(&data, 0.90)); // 8.2 }
HW7 Connection: This is the
quantile()function in Part 3 specifically forf64values!
Interquartile Range (IQR)
IQR = Q3 - Q1 measures the spread of the middle 50% of data.
Uses:
- Less sensitive to outliers than using the range (max - min)
- Outlier detection:
- , or
#![allow(unused)] fn main() { fn iqr(data: &[f64]) -> Option<f64> { let q1 = quantile(data, 0.25)?; let q3 = quantile(data, 0.75)?; Some(q3 - q1) } fn quantile(data: &[f64], q: f64) -> Option<f64> { if data.is_empty() || !(0.0..=1.0).contains(&q) { return None; } let mut sorted = data.to_vec(); sorted.sort_by(|a, b| a.partial_cmp(b).unwrap()); let pos = q * (sorted.len() - 1) as f64; let lower = pos.floor() as usize; let upper = pos.ceil() as usize; if lower == upper { Some(sorted[lower]) } else { let fraction = pos - lower as f64; Some(sorted[lower] * (1.0 - fraction) + sorted[upper] * fraction) } } let data = vec![1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0]; let iqr_val = iqr(&data).unwrap(); let q1 = quantile(&data, 0.25).unwrap(); let q3 = quantile(&data, 0.75).unwrap(); println!("Q1: {}, Q3: {}, IQR: {}", q1, q3, iqr_val); // Outlier bounds let lower_bound = q1 - 1.5 * iqr_val; let upper_bound = q3 + 1.5 * iqr_val; println!("Outlier bounds: [{:.1}, {:.1}]", lower_bound, upper_bound); }
Reminder: The `?` operator is used to propagate errors up the call stack.
- It is equivalent to `return Err(e)` if the expression is an `Err(e)`.
- It is equivalent to `return Ok(x)` if the expression is an `Ok(x)`.
- It is equivalent to `return x` if the expression is a value.
IQR with outliers
Let's use a slightly more interesting dataset:
#![allow(unused)] fn main() { fn iqr(data: &[f64]) -> Option<f64> { let q1 = quantile(data, 0.25)?; let q3 = quantile(data, 0.75)?; Some(q3 - q1) } fn quantile(data: &[f64], q: f64) -> Option<f64> { if data.is_empty() || !(0.0..=1.0).contains(&q) { return None; } let mut sorted = data.to_vec(); sorted.sort_by(|a, b| a.partial_cmp(b).unwrap()); let pos = q * (sorted.len() - 1) as f64; let lower = pos.floor() as usize; let upper = pos.ceil() as usize; if lower == upper { Some(sorted[lower]) } else { let fraction = pos - lower as f64; Some(sorted[lower] * (1.0 - fraction) + sorted[upper] * fraction) } } let data = vec![-1.0, 2.0, 4.4, 6.7, 11.2, 22.8, 83.1, 124.7]; let iqr_val = iqr(&data).unwrap(); let q1 = quantile(&data, 0.25).unwrap(); let q3 = quantile(&data, 0.75).unwrap(); println!("Q1: {}, Q3: {}, IQR: {}", q1, q3, iqr_val); // Outlier bounds let lower_bound = q1 - 1.5 * iqr_val; let upper_bound = q3 + 1.5 * iqr_val; println!("Outlier bounds: [{:.1}, {:.1}]", lower_bound, upper_bound); }
Ranking Algorithms
Standard Rank: Position in sorted order (ties get same rank, gaps follow)
Dense Rank: Position in sorted order (ties get same rank, no gaps)
Values: [100, 95, 95, 90, 85]
Standard: [ 1, 2, 2, 4, 5] ← gap after ties
Dense: [ 1, 2, 2, 3, 4] ← no gaps
Standard and Dense Ranking in Sports
Out of curiosity, I asked Anthropic Opus 4.5 to find examples of standard and dense ranking in sports.
Standard Competition Ranking (1, 2, 2, 4) — Skips positions after ties
Most individual sports and races use this method:
-
Golf ⛳ — The classic example. You'll see "T2" (tied for 2nd) on leaderboards, and the next player is listed as 4th if two players tied for 2nd. This emphasizes that a player finished ahead of X competitors.
-
Tennis (ATP/WTA rankings) 🎾 — Points-based rankings, but when ties occur in tournament results, standard ranking applies.
-
Olympic events 🏅 — Track & field, swimming, skiing, etc. If two athletes tie for silver, no bronze is awarded (they give two silvers). The next finisher is 4th.
-
Marathon / Running races 🏃 — If two runners tie for 2nd, the next finisher is 4th place.
-
Horse racing 🐎 — Finish positions follow standard ranking.
-
Cycling (race stages) 🚴 — Stage finishes use standard ranking.
Dense Ranking (1, 2, 2, 3) — Consecutive positions, no gaps
Less common in sports, but used in some contexts:
-
Soccer/Football league tables ⚽ — While ties on points are typically broken by goal difference (so ties are rare), some leagues display positions using dense-style numbering during the season.
-
Some fitness leaderboards — Particularly in CrossFit or gym competitions where continuous ranking is preferred.
-
Some esports standings — Varies by organization.
Key Insight
The distinction often comes down to what the rank is meant to communicate:
| Standard Rank | Dense Rank |
|---|---|
| "How many competitors finished ahead of you?" | "What tier/bracket are you in?" |
| Emphasizes individual achievement | Emphasizes grouping/classification |
Golf's use of standard ranking makes intuitive sense: if you tied for 2nd, there's still only one person who beat you, but two people share a position ahead of the 4th-place finisher—so that finisher had 3 people beat them.
Implementing Dense Rank
#![allow(unused)] fn main() { fn dense_rank(data: &[f64]) -> Vec<usize> { if data.is_empty() { return vec![]; } // Create (index, value) pairs and sort by value let mut indexed: Vec<(usize, f64)> = data.iter() .enumerate() // produces iter of (index, &value) pairs .map(|(i, &v)| (i, v)) // extract index and dereference value .collect(); // sort by the values (second element of the tuples) indexed.sort_by(|a, b| a.1.partial_cmp(&b.1).unwrap()); // Assign dense ranks let mut ranks = vec![0; data.len()]; let mut current_rank = 0; let mut prev_value: Option<f64> = None; for &(original_idx, value) in &indexed { if let Some(prev) = prev_value { // compare with some small epsilon to avoid floating point // precision issues (e.g. 1.0 and 1.0000000000000001) if (value - prev).abs() > 1e-10 { current_rank += 1; // Only increment for new values } } ranks[original_idx] = current_rank; prev_value = Some(value); } ranks } let scores = vec![85.0, 95.0, 90.0, 95.0, 80.0]; let ranks = dense_rank(&scores); for (score, rank) in scores.iter().zip(ranks.iter()) { println!("Score: {}, Rank: {}", score, rank); } }
HW7 Connection: This is the
dense_rank()function in Part 3!
Part 2: Graph Representation
What is a Graph?
A graph G = (V, E) consists of:
- Vertices (V): nodes/points
- Edges (E): connections between vertices
0 --- 1
| |
| |
3 --- 2
Vertices: {0, 1, 2, 3}
Edges: {(0,1), (1,2), (2,3), (3,0)}
Adjacency List Representation
Store graph as a list of neighbors for each vertex:
#![allow(unused)] fn main() { use std::collections::HashMap; // Using Vec<Vec<usize>> fn create_graph_vec(n: usize, edges: &[(usize, usize)]) -> Vec<Vec<usize>> { let mut adj = vec![vec![]; n]; for &(u, v) in edges { adj[u].push(v); adj[v].push(u); // For undirected graph } adj } // Using HashMap for sparse or labeled graphs fn create_graph_map<'a>(edges: &[(&'a str, &'a str)]) -> HashMap<&'a str, Vec<&'a str>> { let mut adj: HashMap<&'a str, Vec<&'a str>> = HashMap::new(); for &(u, v) in edges { adj.entry(u).or_default().push(v); adj.entry(v).or_default().push(u); } adj } // Example: Square graph let edges = vec![(0, 1), (1, 2), (2, 3), (3, 0)]; let graph = create_graph_vec(4, &edges); for (vertex, neighbors) in graph.iter().enumerate() { println!("Vertex {}: neighbors = {:?}", vertex, neighbors); } let edges_map = vec![("0", "1"), ("1", "2"), ("2", "3"), ("3", "0")]; let graph_map = create_graph_map(&edges_map); for (vertex, neighbors) in graph_map.iter() { println!("Vertex {}: neighbors = {:?}", vertex, neighbors); } }
When to Use Each Representation
| Representation | Best For | Lookup | Memory |
|---|---|---|---|
Vec<Vec<usize>> | Dense graphs, integer vertices | O(1) | O(V + E) |
HashMap<K, Vec<K>> | Sparse graphs, labeled vertices | O(1) avg | O(V + E) |
Part 3: Graph Traversal with BFS and DFS
Breadth-First Search (BFS)
BFS explores nodes level by level using a queue (VecDeque):
Graph: BFS from vertex 0:
0 Level 0: [0]
/ \ Level 1: [1, 3] (neighbors of 0)
1 3 Level 2: [2] (unvisited neighbors)
\ /
2 Visit order: 0 → 1 → 3 → 2
BFS Implementation
This BFS implementation uses a HashSet to track visited nodes and a VecDeque as a FIFO queue. Starting from a given vertex, it repeatedly dequeues the front node, marks it visited, and enqueues all unvisited neighbors. The algorithm returns nodes in the order they were first discovered, which corresponds to visiting vertices level by level outward from the start.
#![allow(unused)] fn main() { use std::collections::{VecDeque, HashSet}; fn bfs(graph: &[Vec<usize>], start: usize) -> Vec<usize> { let mut visited = HashSet::new(); let mut queue = VecDeque::new(); let mut order = Vec::new(); queue.push_back(start); visited.insert(start); while let Some(current) = queue.pop_front() { order.push(current); for &neighbor in &graph[current] { if !visited.contains(&neighbor) { visited.insert(neighbor); queue.push_back(neighbor); } } } order } // Square graph with diagonal // 0 --- 3 // | | // | | // 1 --- 2 let graph = vec![ vec![1, 3], // 0 vec![0, 2], // 1 vec![1, 3], // 2 vec![0, 2], // 3 ]; let order = bfs(&graph, 0); println!("BFS order from 0: {:?}", order); }
Note: VecDeque is essential for O(1) queue operations!
BFS for Shortest Path (Unweighted)
Why does BFS find shortest paths? Because BFS explores nodes level by level, the first time we reach any node is guaranteed to be via the shortest path. When we visit a node at distance d from the start, we've already visited all nodes at distances 0, 1, ..., d-1. This means we can't later find a shorter path to that node.
Key insight: In an unweighted graph, "shortest path" means fewest edges. BFS naturally discovers nodes in order of increasing distance from the start.
#![allow(unused)] fn main() { use std::collections::{VecDeque, HashMap}; fn bfs_distances(graph: &[Vec<usize>], start: usize) -> HashMap<usize, usize> { let mut distances = HashMap::new(); let mut queue = VecDeque::new(); queue.push_back(start); distances.insert(start, 0); while let Some(current) = queue.pop_front() { let current_dist = distances[¤t]; for &neighbor in &graph[current] { if !distances.contains_key(&neighbor) { distances.insert(neighbor, current_dist + 1); queue.push_back(neighbor); } } } distances } let graph = vec![ vec![1, 3], // 0 vec![0, 2], // 1 vec![1, 3], // 2 vec![0, 2], // 3 ]; let distances = bfs_distances(&graph, 0); for (node, dist) in &distances { println!("Distance from 0 to {}: {}", node, dist); } }
Depth-First Search (DFS)
DFS explores as deep as possible first using a stack (Vec or recursion):
Graph: DFS from vertex 0:
0 Step 1: Visit 0, push neighbors [1,3]
/ \ Step 2: Pop 1, visit it, push neighbor [2]
1 3 Step 3: Pop 2, visit it, push neighbor [3]
\ / Step 4: Pop 3, visit it (no new neighbors)
2
Visit order: 0 → 1 → 2 → 3
(Goes deep before exploring siblings)
DFS Implementation (Iterative)
This iterative DFS uses a Vec as a LIFO stack and a HashSet to track visited nodes. Starting from a given vertex, it pops the top node, marks it visited if not already seen, and pushes all unvisited neighbors onto the stack. Neighbors are added in reverse order to maintain consistent left-to-right traversal. The algorithm explores as deep as possible along each branch before backtracking.
#![allow(unused)] fn main() { use std::collections::HashSet; fn dfs(graph: &[Vec<usize>], start: usize) -> Vec<usize> { let mut visited = HashSet::new(); let mut stack = vec![start]; // Use Vec as stack let mut order = Vec::new(); while let Some(current) = stack.pop() { if visited.contains(¤t) { continue; } visited.insert(current); order.push(current); // Add neighbors to stack (reverse for consistent ordering) for &neighbor in graph[current].iter().rev() { if !visited.contains(&neighbor) { stack.push(neighbor); } } } order } let graph = vec![ vec![1, 3], // 0 vec![0, 2], // 1 vec![1, 3], // 2 vec![0, 2], // 3 ]; let order = dfs(&graph, 0); println!("DFS order from 0: {:?}", order); }
BFS vs DFS Summary
| Feature | BFS | DFS |
|---|---|---|
| Data Structure | Queue (VecDeque) | Stack (Vec) |
| Order | Level by level | Deep first |
| Shortest path | ✅ (unweighted) | ❌ |
| Memory | O(width) | O(depth) |
| Use case | Shortest path, levels | Cycle detection, components |
Part 4: Algorithm Design Patterns
We'll cover the following patterns:
- Split-Apply-Combine
- Greedy Algorithms
- Divide and Conquer
Let's start with the first pattern: Split-Apply-Combine.
Pattern 1: Split-Apply-Combine
Already covered in HW7 Part 2 with GroupedSeries:
1. SPLIT: Group data by category
2. APPLY: Calculate aggregate per group
3. COMBINE: Collect results
data = [(A, 10), (B, 20), (A, 30), (B, 40)]
↓ SPLIT
groups = {A: [10, 30], B: [20, 40]}
↓ APPLY (mean)
means = {A: 20.0, B: 30.0}
↓ COMBINE
result = HashMap with means
Pattern 2: Greedy Algorithms
Greedy: Make the locally optimal choice at each step.
Example: Coin change (when it works)
#![allow(unused)] fn main() { fn greedy_coin_change(amount: u32, coins: &[u32]) -> Vec<u32> { let mut result = Vec::new(); let mut remaining = amount; // Sort coins in descending order let mut sorted_coins = coins.to_vec(); sorted_coins.sort_by(|a, b| b.cmp(a)); for &coin in &sorted_coins { while remaining >= coin { result.push(coin); remaining -= coin; } } result } let coins = vec![25, 10, 5, 1]; // US coins let change = greedy_coin_change(67, &coins); println!("67 cents: {:?}", change); // [25, 25, 10, 5, 1, 1] }
Greedy Coin Change is Not Always Optimal
Warning: Greedy doesn't always give optimal solutions!
The greedy approach to the coin change problem is not always optimal when the coin denominations are not in a canonical system. A canonical system is a system of coin denominations where each denomination is at least twice the value of the next smaller denomination.
For example, consider the coin denominations [25, 15, 1] and we want to make change of 30 cents.
#![allow(unused)] fn main() { fn greedy_coin_change(amount: u32, coins: &[u32]) -> Vec<u32> { let mut result = Vec::new(); let mut remaining = amount; // Sort coins in descending order let mut sorted_coins = coins.to_vec(); sorted_coins.sort_by(|a, b| b.cmp(a)); for &coin in &sorted_coins { while remaining >= coin { result.push(coin); remaining -= coin; } } result } let coins = vec![25, 15, 1]; let change = greedy_coin_change(30, &coins); println!("30 cents: {:?}", change); // [25, 1, 1, 1, 1, 1] }
Pattern 3: Divide and Conquer
Divide and Conquer:
- Divide problem into smaller subproblems
- Conquer subproblems recursively
- Combine solutions
Classic example: Binary Search
#![allow(unused)] fn main() { fn binary_search(sorted: &[i32], target: i32) -> Option<usize> { let mut left = 0; let mut right = sorted.len(); while left < right { let mid = left + (right - left) / 2; match sorted[mid].cmp(&target) { std::cmp::Ordering::Equal => return Some(mid), std::cmp::Ordering::Less => left = mid + 1, std::cmp::Ordering::Greater => right = mid, } } None } let data = vec![1, 3, 5, 7, 9, 11, 13, 15]; println!("Index of 7: {:?}", binary_search(&data, 7)); // Some(3) println!("Index of 8: {:?}", binary_search(&data, 8)); // None }
If we just searched item by item we would need O(n) time. Binary search gives us O(log n) time assuming the data is sorted which we get if we use a sorted data structure like BTreeMap. Otherwise we would need to sort the data first which is O(n log n) time.
Algorithm Design Summary
| Pattern | Key Idea | When to Use |
|---|---|---|
| Split-Apply-Combine | Group, aggregate, collect | Data aggregation by category |
| Greedy | Best local choice | Optimization with greedy property |
| Divide & Conquer | Split, solve, merge | Problems with optimal substructure |
Summary: HW7 Algorithm Connections
| HW7 Component | Concepts Used |
|---|---|
| FrequencyTable | Counting, Entry API |
| GroupedSeries | Split-apply-combine, closures |
| Histogram | BTreeMap, binning |
| quantile/iqr | Sorting, interpolation |
| RollingBuffer | VecDeque, circular buffer |
| rank/dense_rank | Sorting, index tracking |
Key Takeaways
- Quantiles require sorted data and linear interpolation
- IQR is robust to outliers (Q3 - Q1)
- BFS uses VecDeque, finds shortest paths
- DFS uses Vec as stack, explores deeply
- Algorithm patterns help structure solutions
In-Class Exercise: Outlier Detection
Task: Implement a function that finds all outliers in a dataset using the IQR method covered earlier in this lecture.
Recall: A value is an outlier if it falls outside the bounds:
- Lower bound: Q1 - 1.5 × IQR
- Upper bound: Q3 + 1.5 × IQR
fn find_outliers(data: &[f64]) -> Vec<f64> {
// TODO: Return a Vec containing all outlier values
// Hint: You can use the quantile() function from earlier
// Step 1: Calculate Q1 and Q3
// Step 2: Calculate IQR
// Step 3: Calculate bounds
// Step 4: Filter and collect outliers
todo!()
}
// Example:
// data = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 100.0]
// Q1 = 2.25, Q3 = 6.25, IQR = 4.0
// Lower bound = 2.25 - 6.0 = -3.75
// Upper bound = 6.25 + 6.0 = 12.25
// Output: [100.0] (only 100.0 is outside the bounds)Hints:
- First implement or copy the
quantile()function from the slides - Use
.iter().filter().cloned().collect()to find values outside bounds - Remember to handle the empty data case
Solution
#![allow(unused)] fn main() { fn quantile(data: &[f64], q: f64) -> Option<f64> { if data.is_empty() || !(0.0..=1.0).contains(&q) { return None; } let mut sorted = data.to_vec(); sorted.sort_by(|a, b| a.partial_cmp(b).unwrap()); let pos = q * (sorted.len() - 1) as f64; let lower = pos.floor() as usize; let upper = pos.ceil() as usize; if lower == upper { Some(sorted[lower]) } else { let fraction = pos - lower as f64; Some(sorted[lower] * (1.0 - fraction) + sorted[upper] * fraction) } } fn find_outliers(data: &[f64]) -> Vec<f64> { if data.is_empty() { return vec![]; } // Step 1: Calculate Q1 and Q3 let q1 = quantile(data, 0.25).unwrap(); let q3 = quantile(data, 0.75).unwrap(); // Step 2: Calculate IQR let iqr = q3 - q1; // Step 3: Calculate bounds let lower_bound = q1 - 1.5 * iqr; let upper_bound = q3 + 1.5 * iqr; // Step 4: Filter and collect outliers data.iter() .filter(|&&x| x < lower_bound || x > upper_bound) .cloned() .collect() } // Test it let data = vec![1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 100.0]; let outliers = find_outliers(&data); let q1 = quantile(&data, 0.25).unwrap(); let q3 = quantile(&data, 0.75).unwrap(); let iqr = q3 - q1; println!("Q1: {}, Q3: {}, IQR: {}", q1, q3, iqr); println!("Lower bound: {}", q1 - 1.5 * iqr); println!("Upper bound: {}", q3 + 1.5 * iqr); println!("Outliers: {:?}", outliers); // Test with data that has outliers on both ends let data2 = vec![-50.0, 10.0, 12.0, 14.0, 15.0, 16.0, 18.0, 200.0]; println!("\nData with outliers on both ends:"); println!("Outliers: {:?}", find_outliers(&data2)); }
Key insights:
- Reuses the
quantile()function from earlier in the lecture - The filter closure uses
&&xbecause we're iterating over&f64references .cloned()converts&f64tof64before collecting- This pattern (compute statistics, then filter) is common in data science
HW7 Brings It All Together
HW7 combines everything:
- Generics and traits (Numeric)
- Collections (HashMap, HashSet, BTreeMap, VecDeque)
- Closures (aggregation functions)
- Iterators (data processing)
- Algorithm design (statistics, grouping)
Good luck on HW7!
A1 FA25 Final Exam Review
Table of Contents:
- Preliminaries
- 1. HashMap and the Entry API
- 2. HashSet and Set Operations
- 3. BTreeMap and Ordered Collections
- 4. VecDeque and Circular Buffers
- 5. Iterators and Iterator Chains
- 6. Algorithm Complexity
- 7. Option and Result Types
- Final Tips for the Exam
Suggested way to use this review material
- The material is organized by major topics.
- For each topic, there are:
- high level overview
- examples
- true/false questions
- find the bug questions
- predict the output questions
- coding challenges
- Try to answer the questions without peeking at the solutions.
- This material focuses on the topics covered in the final third of the course, building on what you learned for midterms 1 and 2.
Exam Format:
The exam will be in four parts:
- Part 1 (10 pts): 5 questions, 2 points each -- select all that are true
- Part 2 (16 pts): 4 questions, 4 points each -- find the bug in the code and fix it
- Part 3 (12 pts): 4 questions, 3 points each -- Predict the output and explain why
- Part 4 (12 pts): 2 questions, 6 points each -- hand-coding problems
Total Points: 50
Suggested time budget for each part:
- Part 1: (~10 min)
- Part 2: (~16 min)
- Part 3: (~12 min)
- Part 4: (~22 min)
for a total of 60 minutes and then another 60 minutes to check your work (if needed).
Preliminaries
The final exam is cumulative but emphasizes the material from the final third of the course. You should be comfortable with:
- Basic Rust syntax (functions, variables, types) (see midterm 1 review)
- Structs, enums, and pattern matching
- Ownership, borrowing, and references
- Generics and traits
- Iterators and closures
See a1 midterm 2 review for more details.
This review focuses on new material: collections (HashMap, HashSet, BTreeMap, VecDeque) and algorithm complexity.
References and Dereferencing
When References Are Created
References are created with &:
#![allow(unused)] fn main() { let x = 5; let r = &x; // r is &i32 let s = "hello"; // s is already &str (string slice) let v = vec![1, 2, 3]; let slice = &v[..]; // slice is &[i32] }
And are common patterns in Rust code. For example, to sum a slice of integers:
#![allow(unused)] fn main() { fn process_ints(ints: &[i32]) -> i32 { let mut sum = 0; for int in ints { sum += *int; } sum } let ints = [1, 2, 3]; println!("sum: {}", process_ints(&ints)); }
When Double References (&&) Occur
Double references commonly appear when:
Iterating over a slice of references:
#![allow(unused)] fn main() { fn process(words: &[&str]) { for word in words { // word is &&str // Rust auto-dereferences `word: &&str` to `word: &str` print!("word: {}, len: {} ", word, word.len()); } println!(); } let words = vec!["art", "bees"]; process(&words); }
Automatic Dereferencing
Rust automatically dereferences in several situations:
1. Method calls (auto-deref):
#![allow(unused)] fn main() { let s = String::from("hello"); let r = &s; let rr = &&s; // All of these work - Rust auto-derefs to call len() s.len(); // String::len(&s) r.len(); // auto-derefs &String to String rr.len(); // auto-derefs &&String through &String to String }
2. Deref coercion in function arguments:
#![allow(unused)] fn main() { fn print_len(s: &str) { println!("{}", s.len()); } let owned = String::from("hello"); print_len(&owned); // &String coerces to &str automatically print_len("hello"); // Already a &str }
3. Comparison operators:
#![allow(unused)] fn main() { let x = 5; let r = &x; // assert!(r == 5); // ERROR! r is a reference, not a value assert!(r == &5); // Compares values, not addresses, but types must match assert!(*r == 5); // Explicit deref to i32 also works }
When Explicit Dereferencing (*) Is Required
1. Assigning to or modifying the underlying value:
#![allow(unused)] fn main() { let mut x = 5; let r = &mut x; *r += 1; // Must deref to modify x println!("x: {}", x); }
2. When types don't match and coercion doesn't apply:
#![allow(unused)] fn main() { let words: &[&str] = &["a", "b"]; for word in words { // word is &&str, but HashMap wants &str as key let key: &str = *word; // Explicit deref needed } }
3. Using entry() or insert() with reference keys:
#![allow(unused)] fn main() { use std::collections::HashMap; fn count<'a>(words: &[&'a str]) -> HashMap<&'a str, i32> { let mut map = HashMap::new(); for word in words { // word: &&str *map.entry(*word) // *word dereferences &&str to &str .or_insert(0) += 1; } map } let words = vec!["a", "b"]; println!("{:?}", count(&words)); println!("{:?}", words); }
Quick Reference Table
| Situation | Type | Need explicit *? |
|---|---|---|
| Method calls | &T, &&T, etc. | No (auto-deref) |
Deref coercion (&String → &str) | Function args | No |
Modifying through &mut T | *r = value | Yes |
HashMap key from &&str | entry(*word) | Yes |
| Pattern matching | &x pattern | Alternative to * |
1. HashMap and the Entry API
Module(s)
Quick Review
HashMap<K, V> is a hash table that maps keys to values:
- Keys must implement
HashandEqtraits - O(1) average lookup, insertion, and deletion
- Does NOT maintain insertion order
f64cannot be used directly as a key (doesn't implementHashdue to NaN)
Key Methods:
insert(key, value)- inserts or overwritesget(&key)- returnsOption<&V>get_mut(&key)- returnsOption<&mut V>contains_key(&key)- returnsboolremove(&key)- removes and returnsOption<V>
The Entry API is the idiomatic way to insert-or-update:
#![allow(unused)] fn main() { *map.entry(key).or_insert(default) += 1; }
.entry(key)returns anEntryenum, which can be eitherOccupiedorVacant- Entry API methods:
or_insert(default)inserts the default value if the key is not presentor_insert_with(f)inserts the value returned by the function if the key is not presentor_default()inserts the default value for the type if the key is not presentand_modify(f)modifies the value if the key is present
Examples
#![allow(unused)] fn main() { use std::collections::HashMap; // Basic HashMap usage let mut scores = HashMap::new(); // .insert returns None if the key was not in the map let mut result = scores.insert("Alice", 85); println!("result: {:?}", result); // None, because "Alice" was not in the map // .insert() returns Some(&value), where value is the old value if the key was // already in the map result = scores.insert("Alice", 87); println!("result: {:?}", result); // Some(&85) scores.insert("Bob", 90); // get() returns Option println!("scores.get(\"Alice\"): {:?}", scores.get("Alice")); // Some(&85) println!("scores.get(\"Carol\"): {:?}", scores.get("Carol")); // None // unwrap_or provides a default println!("scores.get(\"Carol\").unwrap_or(&0): {:?}", scores.get("Carol").unwrap_or(&0)); // &0 }
#![allow(unused)] fn main() { use std::collections::HashMap; // Entry API for counting let mut word_counts = HashMap::new(); for word in ["apple", "banana", "apple"] { *word_counts.entry(word).or_insert(0) += 1; } // word_counts: {"apple": 2, "banana": 1} println!("word_counts: {:?}", word_counts); }
#![allow(unused)] fn main() { use std::collections::HashMap; // Entry API - or_insert only inserts if key is missing let mut map = HashMap::new(); *map.entry("a").or_insert(0) += 1; // a = 1 *map.entry("a").or_insert(10) += 1; // a = 2 (10 is NOT used, key exists) println!("map: {:?}", map); }
True/False Questions
-
T/F: Keys in a HashMap must implement the
HashandEqtraits. -
T/F: HashMap maintains insertion order of elements.
-
T/F:
f64can be used directly as a HashMap key. -
T/F: The
entry()API allows efficient insert-or-update operations. -
T/F:
map.get(&key)returnsVdirectly. -
T/F: Looking up a value by key in a HashMap is O(1) on average.
Answers
- True - HashMap requires Hash and Eq traits for keys
- False - HashMap does not maintain insertion order (use IndexMap for that)
- False - f64 doesn't implement Hash due to NaN issues; use OrderedFloat
- True - The entry() API is designed for efficient insert-or-update patterns
- False - get() returns Option<&V>, not V directly
- True - HashMap lookup is O(1) average case
Find the Bug
Question 1:
#![allow(unused)] fn main() { use std::collections::HashMap; fn count_words<'a>(words: &[&'a str]) -> HashMap<&'a str, i32> { let mut counts = HashMap::new(); for word in words { counts.entry(word).or_insert(0) += 1; } counts } }
Answer
Bug: We need to dereference the key word to get the &str, not the &&str
and then dereference counts... so we can modify the value.
Fix:
#![allow(unused)] fn main() { use std::collections::HashMap; fn count_words<'a>(words: &[&'a str]) -> HashMap<&'a str, i32> { let mut counts = HashMap::new(); for word in words { *counts.entry(*word).or_insert(0) += 1; } counts } }
Question 2:
#![allow(unused)] fn main() { use std::collections::HashMap; fn merge_maps(map1: HashMap<String, i32>, map2: HashMap<String, i32>) -> HashMap<String, i32> { let mut result = map1; for (key, value) in map2 { result.insert(key, result.get(&key).unwrap() + value); } result } }
Answer
Bug: Using get(&key).unwrap() on a key that might not exist in result (map1). If a key from map2 is not in map1, this panics.
Fix:
#![allow(unused)] fn main() { use std::collections::HashMap; fn merge_maps(map1: HashMap<String, i32>, map2: HashMap<String, i32>) -> HashMap<String, i32> { let mut result = map1; for (key, value) in map2 { *result.entry(key).or_insert(0) += value; } result } }
Predict the Output
Question 1:
use std::collections::HashMap; fn main() { let mut scores = HashMap::new(); scores.insert("Alice", 85); scores.insert("Bob", 90); scores.insert("Alice", 95); let alice_score = scores.get("Alice").unwrap_or(&0); let carol_score = scores.get("Carol").unwrap_or(&0); println!("{} {}", alice_score, carol_score); }
Answer
Output: 95 0
Reasoning:
- "Alice" is inserted twice. The second insert (95) overwrites the first (85).
get("Alice")returns Some(&95), unwrap_or gives 95get("Carol")returns None, unwrap_or provides default &0
Question 2:
use std::collections::HashMap; fn main() { let mut map: HashMap<&str, i32> = HashMap::new(); *map.entry("a").or_insert(0) += 1; *map.entry("b").or_insert(5) += 1; *map.entry("a").or_insert(10) += 1; let a = map.get("a").unwrap(); let b = map.get("b").unwrap(); println!("{} {}", a, b); }
Answer
Output: 2 6
Reasoning:
- First entry("a"): key doesn't exist, inserts 0, then += 1 → a = 1
- entry("b"): key doesn't exist, inserts 5, then += 1 → b = 6
- Second entry("a"): key exists (value 1), or_insert(10) does NOT insert, just returns &mut to existing value, then += 1 → a = 2
Coding Challenge
Challenge: Implement most_frequent
Write a function that takes a slice of integers and returns the value that appears most frequently. Return None if the slice is empty.
use std::collections::HashMap; fn most_frequent(numbers: &[i32]) -> Option<i32> { // Your code here } fn main() { let nums = vec![1, 2, 2, 3, 3, 3, 4]; println!("{:?}", most_frequent(&nums)); // Should print Some(3) println!("{:?}", most_frequent(&[])); // Should print None }
Solution
use std::collections::HashMap; fn most_frequent(numbers: &[i32]) -> Option<i32> { if numbers.is_empty() { return None; } let mut counts = HashMap::new(); for &num in numbers { *counts.entry(num).or_insert(0) += 1; } counts.into_iter() .max_by_key(|&(_, count)| count) .map(|(num, _)| num) } fn main() { let nums = vec![1, 2, 2, 3, 3, 3, 4]; println!("{:?}", most_frequent(&nums)); // Should print Some(3) println!("{:?}", most_frequent(&[])); // Should print None }
2. HashSet and Set Operations
Quick Review
HashSet
- Elements must implement
HashandEqtraits - O(1) average lookup, insertion, deletion
- Automatically removes duplicates
- Does NOT maintain insertion order
Key Methods:
insert(value)- returnsbool(true if new)contains(&value)- returnsbool(true if value is in the set)remove(&value)- returnsbool(true if value was in the set)
Set Operations:
intersection(&other)- returns a set with elements in both setsunion(&other)- returns a set with elements in either setdifference(&other)- returns a set with elements in self but not othersymmetric_difference(&other)- returns a set with elements in one but not both
Examples
#![allow(unused)] fn main() { use std::collections::HashSet; // Creating HashSets let set1: HashSet<i32> = vec![1, 2, 3, 4].into_iter().collect(); let set2: HashSet<i32> = vec![3, 4, 5, 6].into_iter().collect(); // Set operations let inter: HashSet<_> = set1.intersection(&set2).copied().collect(); println!("inter: {:?}", inter); // inter = {3, 4} let uni: HashSet<_> = set1.union(&set2).copied().collect(); println!("uni: {:?}", uni); // uni = {1, 2, 3, 4, 5, 6} let diff: HashSet<_> = set1.difference(&set2).copied().collect(); println!("diff: {:?}", diff); // diff = {1, 2} (in set1 but not set2) let sym_diff: HashSet<_> = set1.symmetric_difference(&set2).copied().collect(); println!("sym_diff: {:?}", sym_diff); // sym_diff = {1, 2, 5, 6} // Checking membership let has_three = set1.contains(&3); // true println!("has_three: {}", has_three); // HashSet for uniqueness let words = vec!["apple", "banana", "apple", "cherry"]; let unique: HashSet<_> = words.into_iter().collect(); println!("unique: {:?}", unique); // unique = {"apple", "banana", "cherry"} }
True/False Questions
-
T/F: HashSet automatically removes duplicate values.
-
T/F: Elements in a HashSet must implement
HashandEqtraits. -
T/F: HashSet maintains elements in sorted order.
-
T/F: The
intersection()method returns elements common to two sets. -
T/F: Checking if an element exists in a HashSet is O(n).
Answers
- True - HashSet stores only unique values
- True - HashSet requires Hash and Eq traits for elements
- False - HashSet doesn't maintain any particular order (use BTreeSet for sorted)
- True - intersection() returns elements present in both sets
- False - HashSet lookup is O(1) average, not O(n)
Find the Bug
Question:
#![allow(unused)] fn main() { use std::collections::HashSet; fn find_common<T: PartialEq>(set1: &HashSet<T>, set2: &HashSet<T>) -> HashSet<T> { set1.intersection(set2).cloned().collect() } }
Answer
Bug: HashSet requires Hash + Eq trait bounds, not just PartialEq. The function also needs Clone for .cloned().
Fix:
#![allow(unused)] fn main() { use std::collections::HashSet; use std::hash::Hash; fn find_common<T: Hash + Eq + Clone>(set1: &HashSet<T>, set2: &HashSet<T>) -> HashSet<T> { set1.intersection(set2).cloned().collect() } }
Predict the Output
Question:
use std::collections::HashSet; fn main() { let set1: HashSet<&str> = vec!["apple", "banana", "cherry"].into_iter().collect(); let set2: HashSet<&str> = vec!["cherry", "date", "elderberry"].into_iter().collect(); let inter: HashSet<_> = set1.intersection(&set2).copied().collect(); println!("inter: {:?}", inter); let diff: HashSet<_> = set1.difference(&set2).copied().collect(); println!("diff: {:?}", diff); let sym_diff: HashSet<_> = set1.symmetric_difference(&set2).copied().collect(); println!("sym_diff: {:?}", sym_diff); println!("{} {} {}", inter.len(), diff.len(), sym_diff.len()); }
Answer
Output:
inter: {"cherry"}
diff: {"banana", "apple"}
sym_diff: {"elderberry", "apple", "date", "banana"}
1 2 4
Reasoning:
- set1: {"apple", "banana", "cherry"}
- set2: {"cherry", "date", "elderberry"}
- intersection: {"cherry"} → length = 1
- difference (in set1 but not set2): {"apple", "banana"} → length = 2
- symmetric difference: {"apple", "banana", "date", "elderberry"} → length = 4
Coding Challenge
Challenge: Find duplicates
Write a function that takes a slice of integers and returns a Vec containing only the values that appear more than once. The result should not contain duplicates itself.
use std::collections::{HashMap, HashSet}; fn find_duplicates(numbers: &[i32]) -> Vec<i32> { // Your code here } fn main() { let nums = vec![1, 2, 2, 3, 3, 3, 4, 5, 5]; println!("{:?}", find_duplicates(&nums)); // [2, 3, 5] (order may vary) }
Solution
use std::collections::HashSet; fn find_duplicates(numbers: &[i32]) -> Vec<i32> { let mut seen = HashSet::new(); let mut duplicates = HashSet::new(); for &num in numbers { if !seen.insert(num) { // insert returns false if value already existed duplicates.insert(num); } } duplicates.into_iter().collect() } fn main() { let nums = vec![1, 2, 2, 3, 3, 3, 4, 5, 5]; println!("{:?}", find_duplicates(&nums)); // [2, 3, 5] (order may vary) }
3. BTreeMap and Ordered Collections
Quick Review
BTreeMap<K, V> is a sorted map based on B-trees:
- Keys are always in sorted order
- Keys must implement
Ordtrait (not Hash) - O(log n) lookup, insertion, deletion
- Efficient for range queries
- Iteration yields key-value pairs in sorted key order
When to use BTreeMap vs HashMap:
- HashMap: faster single-key operations (O(1) vs O(log n))
- BTreeMap: need sorted order, range queries, or keys don't implement Hash
Examples
#![allow(unused)] fn main() { use std::collections::BTreeMap; let mut map = BTreeMap::new(); map.insert(3, "three"); map.insert(1, "one"); map.insert(4, "four"); // Iteration is in sorted key order for (k, v) in map.iter() { println!("{}: {}", k, v); } // Output: // 1: one // 3: three // 4: four // First and last keys let first = map.keys().next(); // Some(&1) let last = map.keys().last(); // Some(&4) // Range queries for (k, v) in map.range(2..=4) { println!("{}: {}", k, v); } // Output: 3: three, 4: four }
True/False Questions
-
T/F: BTreeMap stores keys in sorted order.
-
T/F: Insertion into a BTreeMap is O(1).
-
T/F: BTreeMap requires keys to implement the
Hashtrait. -
T/F: Iterating over a BTreeMap yields key-value pairs in sorted key order.
-
T/F: BTreeMap is faster than HashMap for all operations.
Answers
- True - BTreeMap keys are always in sorted order
- False - BTreeMap insertion is O(log n), not O(1)
- False - BTreeMap requires Ord trait, not Hash
- True - Iteration yields pairs in sorted key order
- False - HashMap is faster (O(1) vs O(log n)) for single lookups; BTreeMap is better for range queries and ordered iteration
Predict the Output
Question:
use std::collections::BTreeMap; fn main() { let mut scores = BTreeMap::new(); scores.insert("Charlie", 85); scores.insert("Alice", 95); scores.insert("Bob", 90); let first_key = scores.keys().next().unwrap(); let last_key = scores.keys().last().unwrap(); println!("{} {}", first_key, last_key); }
Answer
Output: Alice Charlie
Reasoning:
- BTreeMap stores keys in sorted (alphabetical) order
- Sorted order: Alice, Bob, Charlie
- first key (next()): "Alice"
- last key: "Charlie"
4. VecDeque and Circular Buffers
Quick Review
VecDeque
- O(1) push/pop from both ends
- Implemented as a circular/ring buffer
- Can be used as a stack OR a queue
- Grows dynamically like Vec
Key Methods:
push_front(value)- add to frontpush_back(value)- add to backpop_front()- remove from front, returnsOption<T>pop_back()- remove from back, returnsOption<T>front()/back()- peek without removing
Use Cases:
- Queue (FIFO): push_back + pop_front
- Stack (LIFO): push_back + pop_back
- Rolling windows / circular buffers
Examples
#![allow(unused)] fn main() { use std::collections::VecDeque; let mut deque: VecDeque<i32> = VecDeque::new(); // Building a deque deque.push_back(1); // [1] deque.push_back(2); // [1, 2] deque.push_front(3); // [3, 1, 2] deque.push_back(4); // [3, 1, 2, 4] // Removing elements let front = deque.pop_front(); // Some(3), deque is [1, 2, 4] let back = deque.pop_back(); // Some(4), deque is [1, 2] // Using as a queue (FIFO) let mut queue = VecDeque::new(); queue.push_back("first"); queue.push_back("second"); let next = queue.pop_front(); // Some("first") // Iteration for val in deque.iter() { println!("{}", val); } }
True/False Questions
-
T/F: VecDeque allows efficient O(1) insertion and removal at both ends.
-
T/F: VecDeque is implemented as a circular buffer.
-
T/F: VecDeque can only store elements that implement
Copy. -
T/F:
push_front()andpush_back()are the primary insertion methods. -
T/F: VecDeque maintains elements in sorted order.
-
T/F:
VecDeque::push_front()is O(n).
Answers
- True - VecDeque provides O(1) operations at both ends
- True - VecDeque is implemented as a growable ring/circular buffer
- False - VecDeque can store any type
- True - push_front() and push_back() are the main insertion methods
- False - VecDeque maintains insertion order, not sorted order
- False - VecDeque::push_front() is O(1), that's its main advantage over Vec
Predict the Output
Question 1:
use std::collections::VecDeque; fn main() { let mut buffer: VecDeque<i32> = VecDeque::new(); buffer.push_back(1); buffer.push_back(2); buffer.push_front(3); buffer.push_back(4); buffer.pop_front(); let sum: i32 = buffer.iter().sum(); println!("{}", sum); }
Answer
Output: 7
Reasoning:
- push_back(1): [1]
- push_back(2): [1, 2]
- push_front(3): [3, 1, 2]
- push_back(4): [3, 1, 2, 4]
- pop_front() removes 3: [1, 2, 4]
- sum = 1 + 2 + 4 = 7
Question 2:
use std::collections::VecDeque; fn main() { let mut q: VecDeque<i32> = VecDeque::new(); q.push_back(10); q.push_back(20); q.push_back(30); let first = q.pop_front().unwrap(); q.push_back(first + 5); for val in q.iter() { print!("{} ", val); } println!(); }
Answer
Output: 20 30 15
Reasoning:
- Initial pushes: [10, 20, 30]
- pop_front() removes 10, first = 10
- push_back(10 + 5) adds 15: [20, 30, 15]
- Iteration prints: 20 30 15
Coding Challenge
Challenge: Implement a Rolling Average
Write a function that calculates the running (cumulative) average at each position. The running average at position i is the mean of all elements from index 0 to i.
fn running_average(values: &[f64]) -> Vec<f64> { // Your code here } fn main() { let data = vec![2.0, 4.0, 6.0, 8.0]; let result = running_average(&data); println!("{:?}", result); // Should print [2.0, 3.0, 4.0, 5.0] }
Solution
fn running_average(values: &[f64]) -> Vec<f64> { let mut result = Vec::new(); let mut sum = 0.0; for (i, &value) in values.iter().enumerate() { sum += value; let avg = sum / (i + 1) as f64; result.push(avg); } result } fn main() { let data = vec![2.0, 4.0, 6.0, 8.0]; let result = running_average(&data); println!("{:?}", result); // Should print [2.0, 3.0, 4.0, 5.0] }
5. Iterators and Iterator Chains
Quick Review
Iterator Creation:
iter()- yields&T(immutable references)iter_mut()- yields&mut T(mutable references)into_iter()- consumes collection, yields ownedT
Key Iterator Methods:
map(|x| ...)- transform each elementfilter(|x| ...)- keep elements matching predicatefold(init, |acc, x| ...)- accumulate into single valuecollect()- consume iterator into collectionsum()- sum all elementscount()- count elementstake(n)- take first n elementsskip(n)- skip first n elementsenumerate()- yields(index, value)pairs
Important: Iterator adaptors (map, filter, etc.) are lazy - they don't execute until consumed by a method like collect(), sum(), or for loop.
Examples
#![allow(unused)] fn main() { let numbers = vec![1, 2, 3, 4, 5, 6]; // Filter and map let result: Vec<i32> = numbers.iter() .filter(|&&x| x % 2 == 0) // keep even: [2, 4, 6] .map(|x| x * 2) // double: [4, 8, 12] .collect(); // Sum let sum: i32 = numbers.iter().sum(); // 21 // Filter, map, take let result: Vec<i32> = numbers.iter() .filter(|&&x| x % 2 == 1) // keep odd: [1, 3, 5] .map(|x| x * x) // square: [1, 9, 25] .take(2) // first 2: [1, 9] .collect(); // Enumerate for (i, val) in numbers.iter().enumerate() { println!("Index {}: {}", i, val); } // Fold for custom accumulation let product: i32 = numbers.iter() .fold(1, |acc, x| acc * x); // 720 }
True/False Questions
-
T/F: Iterator methods like
map()andfilter()are lazily evaluated. -
T/F: The
collect()method transforms an iterator into a collection. -
T/F: Calling
.iter()on a Vec transfers ownership of the elements. -
T/F: The
fold()method requires an initial accumulator value. -
T/F: Iterator chains are evaluated from right to left.
Answers
- True - Iterator adaptors are lazy; they don't execute until consumed
- True - collect() consumes the iterator and builds a collection
- False - iter() borrows elements (&T); into_iter() takes ownership
- True - fold() requires an initial value as its first argument
- False - Iterator chains are evaluated left to right (and lazily)
Find the Bug
Question 1:
#![allow(unused)] fn main() { fn double_evens(numbers: &[i32]) -> Vec<i32> { numbers.iter() .filter(|&x| x % 2 == 0) .map(|x| x * 2) } }
Answer
Bug: Missing .collect() at the end of the iterator chain. Iterator adaptors are lazy and return an iterator, not a Vec.
Fix:
#![allow(unused)] fn main() { fn double_evens(numbers: &[i32]) -> Vec<i32> { numbers.iter() .filter(|&x| x % 2 == 0) .map(|x| x * 2) .collect() } }
Question 2:
#![allow(unused)] fn main() { fn sum_positive(numbers: &[i32]) -> i32 { numbers.iter() .filter(|x| x > 0) .sum() } }
Answer
Bug: The filter closure receives &&i32 (reference to reference), but comparing x > 0 tries to compare a reference with an integer.
Fix:
#![allow(unused)] fn main() { fn sum_positive(numbers: &[i32]) -> i32 { numbers.iter() .filter(|&&x| x > 0) // or .filter(|x| **x > 0) .sum() } }
Predict the Output
Question 1:
fn main() { let numbers = vec![1, 2, 3, 4, 5, 6]; let result: Vec<i32> = numbers.iter() .filter(|&x| x % 2 == 1) .map(|x| x * x) .take(2) .collect(); println!("{:?}", result); }
Answer
Output: [1, 9]
Reasoning:
- filter keeps odd numbers: [1, 3, 5]
- map squares them: [1, 9, 25]
- take(2) keeps first 2: [1, 9]
Question 2:
fn main() { let data = vec![10, 20, 30, 40, 50]; let result: i32 = data.iter() .skip(1) .take(3) .filter(|&&x| x > 25) .sum(); println!("{}", result); }
Answer
Output: 70
Reasoning:
- Original: [10, 20, 30, 40, 50]
- skip(1): [20, 30, 40, 50]
- take(3): [20, 30, 40]
- filter(x > 25): [30, 40]
- sum: 30 + 40 = 70
Question 3:
fn main() { let numbers = vec![1, 2, 3, 4, 5]; let sum: i32 = numbers.iter() .enumerate() .filter(|(i, _)| i % 2 == 0) .map(|(_, v)| v) .sum(); println!("{}", sum); }
Answer
Output: 9
Reasoning:
- enumerate gives: [(0,1), (1,2), (2,3), (3,4), (4,5)]
- filter where index % 2 == 0: [(0,1), (2,3), (4,5)]
- map extracts values: [1, 3, 5]
- sum: 1 + 3 + 5 = 9
Coding Challenge
Challenge: Count elements in range
Write a function that counts how many elements in a slice fall within a given range [low, high] (inclusive).
fn count_in_range(numbers: &[i32], low: i32, high: i32) -> usize { // Your code here - use iterator methods } fn main() { let nums = vec![1, 5, 10, 15, 20, 25]; println!("{}", count_in_range(&nums, 5, 20)); // Should print 4 }
Solution
fn count_in_range(numbers: &[i32], low: i32, high: i32) -> usize { numbers.iter() .filter(|&&x| x >= low && x <= high) .count() } fn main() { let nums = vec![1, 5, 10, 15, 20, 25]; println!("{}", count_in_range(&nums, 5, 20)); // Should print 4 }
6. Algorithm Complexity
Quick Review
Big O Notation describes how runtime grows with input size:
| Complexity | Name | Example |
|---|---|---|
| O(1) | Constant | HashMap lookup, Vec::push (amortized) |
| O(log n) | Logarithmic | BTreeMap operations, binary search |
| O(n) | Linear | Linear search, single loop |
| O(n log n) | Linearithmic | Sorting (merge sort, quicksort) |
| O(n²) | Quadratic | Nested loops, bubble sort |
Common Operations:
| Data Structure | Insert | Lookup | Delete |
|---|---|---|---|
| Vec (end) | O(1)* | O(1) | O(1) |
| Vec (middle) | O(n) | O(1) | O(n) |
| HashMap | O(1) | O(1) | O(1) |
| BTreeMap | O(log n) | O(log n) | O(log n) |
| VecDeque (ends) | O(1) | O(1) | O(1) |
*amortized
Graph Algorithms:
- BFS (Breadth-First Search): uses a queue (FIFO)
- DFS (Depth-First Search): uses a stack (LIFO)
True/False Questions
-
T/F: A
Vec::push()operation is O(1) amortized. -
T/F: Searching for a key in a HashMap is O(n) in the average case.
-
T/F: Sorting a vector with
.sort()is O(n log n). -
T/F: Graph BFS traversal uses a queue data structure.
-
T/F: Inserting into a BTreeMap is O(1).
Answers
- True - Vec::push() is amortized O(1) due to capacity doubling
- False - HashMap lookup is O(1) average, not O(n)
- True - Rust's sort uses a modified merge sort, which is O(n log n)
- True - BFS uses a queue (FIFO); DFS uses a stack (LIFO)
- False - BTreeMap insertion is O(log n), not O(1)
7. Option and Result Types
Quick Review
Option
Some(value)- contains a valueNone- no value
Result<T, E> - for operations that might fail:
Ok(value)- success with valueErr(error)- failure with error
Common Methods:
unwrap()- get value or panicunwrap_or(default)- get value or defaultunwrap_or_else(|| ...)- get value or compute default?operator - propagate errors (Result) or None (Option)is_some()/is_ok()- check variantmap(|x| ...)- transform if Some/Ok
Examples
#![allow(unused)] fn main() { // Option let maybe_value: Option<i32> = Some(5); let no_value: Option<i32> = None; let x = maybe_value.unwrap_or(0); // 5 let y = no_value.unwrap_or(0); // 0 // Result fn divide(a: i32, b: i32) -> Result<i32, String> { if b == 0 { Err(String::from("division by zero")) } else { Ok(a / b) } } let result = divide(10, 2); // Ok(5) let error = divide(10, 0); // Err("division by zero") // Using ? to propagate fn calculate(a: i32, b: i32) -> Result<i32, String> { let quotient = divide(a, b)?; // Returns Err early if divide fails Ok(quotient * 2) } }
True/False Questions
-
T/F:
Option::unwrap()will panic if the value isNone. -
T/F: The
?operator can be used to propagate errors fromResult. -
T/F:
Some(5)andNoneare both variants ofOption<i32>. -
T/F:
Result<T, E>is used for operations that might fail with an error. -
T/F:
unwrap_or(default)returns the contained value or a provided default.
Answers
- True - unwrap() panics on None
- True - The ? operator propagates Result errors
- True - Some and None are Option variants
- True - Result is for fallible operations
- True - unwrap_or() provides a default value
Final Tips for the Exam
-
HashMap vs BTreeMap: Use HashMap for fast O(1) lookups. Use BTreeMap when you need sorted keys or range queries.
-
Entry API: Always use
entry().or_insert()for counting patterns instead ofget().unwrap(). -
HashSet trait bounds: Remember that HashSet requires
Hash + Eq, not justPartialEq. -
Iterator laziness: Remember to call
.collect()or another consumer - map/filter alone don't execute! -
Reference patterns in closures:
iter()yields&Tfilter(|x| ...)receives&&Twhen used with iter()- Use
|&x|or|&&x|to destructure
-
VecDeque for both ends: Use VecDeque when you need efficient push/pop from both front and back.
-
Complexity matters: Know that HashMap is O(1), BTreeMap is O(log n), and sorting is O(n log n).
-
Understand references and when to dereference: Remember that iterators yield references, not values.
-
Review the preliminaries as well!
Good luck on your final exam! 🦀
Graph Representation
About This Module
This module introduces graph data structures and various ways to represent graphs in computer programs. You'll learn about different graph representation methods including edge lists, adjacency lists, and adjacency matrices, along with their trade-offs and use cases.
Definition: A graph is a collection of nodes (a.k.a. vertices) connected by edges.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 8.1: Storing Lists of Values with Vectors
- Chapter 8.3: Storing Keys with Associated Values in Hash Maps
- Chapter 6.1: Defining an Enum - For graph node representation
Pre-lecture Reflections
Before class, consider these questions:
- What real-world problems can be modeled as graphs?
- What are the trade-offs between different graph representation methods?
- How does the density of a graph affect the choice of representation?
- When would you choose an adjacency matrix vs. adjacency list?
- How do directed vs. undirected graphs differ in their representation?
Lecture
Learning Objectives
By the end of this module, you should be able to:
- Identify real-world problems that can be modeled as graphs
- Implement three major graph representations: edge lists, adjacency lists, and adjacency matrices
- Choose appropriate graph representations based on problem requirements
- Convert between different graph representation formats
- Understand the space and time complexity trade-offs of each representation
- Handle graphs with non-numeric vertex labels
Graph Definition and Applications
Definition: A graph is a collection of nodes (a.k.a. vertices) connected by edges.
Why are graphs useful?
Lots of problems reduce to graph problems
- The Internet is a graph: nodes are devices that have IP address, routes are edges
- (Example algorithms: Shortest path, min/max flow)
- (how many devices on the internet?)
- The Web is a graph (crawlers) (how many web pages on the internet?)
- Social networks are graphs (graph degrees, k-connectivity)
- Logistics hubs and transportation are graphs (Traveling salesman, subway and bus schedules)
- Computer scheduling (instruction dependencies)
- GSM frequency scheduling (Graph coloring -- no two connected nodes are same color)
- Medical school residency assignments (stable marriage algorithm)
- And many others....
What types of graphs are there?
- Directed vs Undirected
- Weighted (cost on the edge) vs Unweighted (all edges have same cost)
- Special
- Tree (every node has a single parent, no cycles)
- Rooted tree (single parent node, very common and useful, includes heaps, b-trees, tries etc).
- DAG (most workflows are DAGs)
- Bi-partite (can be separated to 2 sides with all edges crossing sides)
- Cliques (every node is connected to every other node)
Graph representations: various options
-
What information we want to access
-
What efficiency required
![[sample image]](modules/images/graph.svg)
Today:
- Edges List
- Vertex Adjacency lists
- Vertex Adjacency matrix
Focus on undirected graphs:
- easy to adjust for directed
Edges List
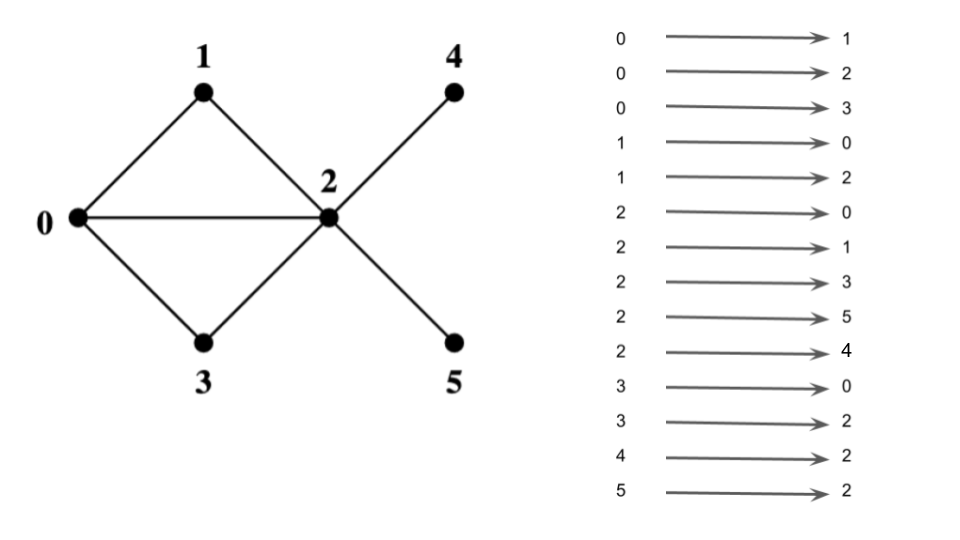
- List of directed or undirected edges
- Can be sorted/ordered for easier access/discovery
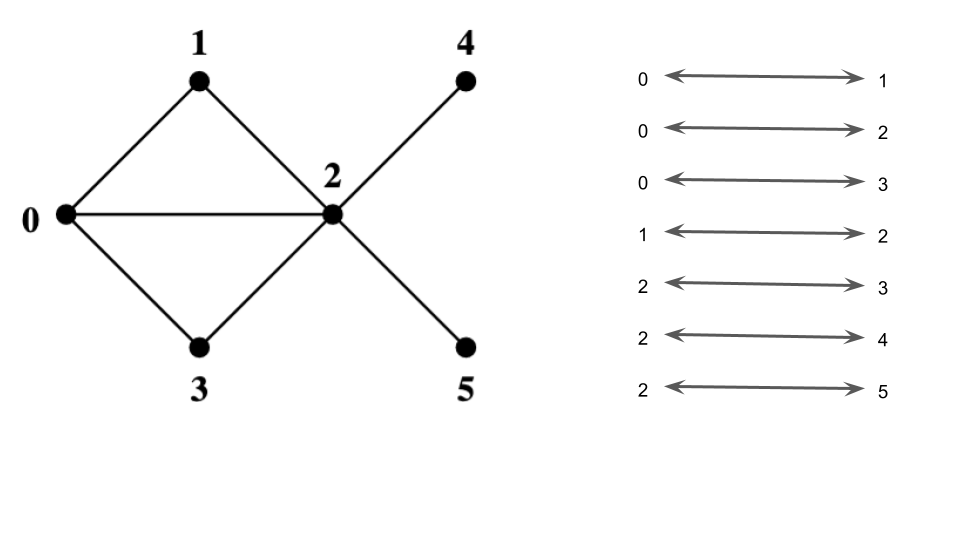
#![allow(unused)] fn main() { // number of vertices let n : usize = 6; // list of edges let edges : Vec<(usize,usize)> = vec![(0,1), (0,2), (0,3), (1,2), (2,3), (2,4), (2,5)]; println!("{:?}", edges); println!("{:?}",edges.binary_search(&(2,3))); println!("{:?}",edges.binary_search(&(1,3))); }
Adjacency lists
For each vertex, store the list of its neighbors
![[sample graph]](modules/images/sparse.png)
Collection:
- classical approach: linked list
- vectors
#![allow(unused)] fn main() { // Create a vector of length n of empty vectors let mut graph_list : Vec<Vec<usize>> = vec![vec![];n]; // iterate through the node pairs for (v,w) in edges.iter() { graph_list[*v].push(*w); graph_list[*w].push(*v); // for undirected, v is also connected to w }; for i in 0..graph_list.len() { println!("{}: {:?}", i, graph_list[i]); }; println!("{:?}", graph_list[2].binary_search(&3)); println!("{:?}", graph_list[1].binary_search(&3)); }
0: [1, 2, 3]
1: [0, 2]
2: [0, 1, 3, 4, 5]
3: [0, 2]
4: [2]
5: [2]
Ok(2)
Err(2)
Adjacency matrix
- vertices
- matrix
- For each pair of vertices, store a boolean value: edge present or not
- Matrix is symmetric for undirected graph

#![allow(unused)] fn main() { // make a vector of n vectors of length n // initialized to false let mut graph_matrix = vec![vec![false;n];n]; // iterate and set entries to true where edges exist for (v,w) in edges.iter() { graph_matrix[*v][*w] = true; graph_matrix[*w][*v] = true; }; for row in &graph_matrix { for entry in row.iter() { print!(" {} ",if *entry {"1"} else {"0"}); } println!(""); }; println!("{}", graph_matrix[2][3]); println!("{}", graph_matrix[1][3]); }
0 1 1 1 0 0
1 0 1 0 0 0
1 1 0 1 1 1
1 0 1 0 0 0
0 0 1 0 0 0
0 0 1 0 0 0
true
false
Sample Graph Recap
![[sample image]](modules/images/graph.svg)
This lecture's graphs:
- undirected
- no self-loops
- self-loop: edge connecting a vertex to itself
- no parallel edges (connecting the same pair of vertices)
Simplifying assumption:
- vertices labeled
What if labels are not in ?
For example:
- nodel labels are not numbers, e.g. strings
Ttype of labels
Solution 1: Map everything to this range (most common)
- Create hash maps from input labels to
- Create a reverse hash map to recover labels when needed
Solution 2: Replace with hash maps and hash sets (less common, harder to use)
- Adjacency lists: use
HashMap<T,Vec<T>>- first node is the key and values is the adjacency list
- Adjacency matrix: use
HashSet<(T,T)>- Sets of tuples where node pairs that are connected are inserted
- Bonus gain:
HashSet<(T,T)>better than adjacency matrix for sparse graphs
What if the graph is directed?
Adjacency lists:
- separate lists incoming/outgoing edges
- depends on what information needed for your algorithm
Adjacency matrix:
- example: edge and no edge in the opposite direction:
matrix[u][v] = truematrix[v][u] = false
- Matrix is no longer symmetric
Graph Algorithms: Counting Triangles
About This Module
This module introduces a fundamental graph algorithm: counting triangles in a graph. You'll learn multiple approaches to solve this problem, understand their complexity trade-offs, and explore real-world applications including spam detection and social network analysis.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 8.1: Storing Lists of Values with Vectors - Review for adjacency lists
- Chapter 6.2: The match Control Flow Construct - For recursive algorithms
- Chapter 4.3: The Slice Type - For iterating over graph data
Pre-lecture Reflections
Before class, consider these questions:
- Why might counting triangles be useful in real-world applications?
- What are the trade-offs between using adjacency matrices vs. adjacency lists?
- How does algorithm complexity change with graph density?
- What strategies can reduce duplicate counting in graph algorithms?
- When would you choose recursion vs. iteration for graph traversal?
Lecture
Learning Objectives
By the end of this module, you should be able to:
- Implement multiple algorithms for counting triangles in graphs
- Analyze the time complexity of different graph algorithms
- Choose appropriate graph representations for specific algorithms
- Handle duplicate counting issues in graph traversal
- Apply triangle counting to real-world problems like spam detection
- Understand the relationship between graph density and algorithm performance
Triangle Counting Problem
Problem to solve: Consider all triples of vertices. What is the number of those in which all vertices are connected? And alternatively how many unique triangles does a vertex belong to?
- Why is this important? Turns out that hosts that contain spam pages have a very different triangle patterns then regular hosts (https://chato.cl/papers/becchetti_2007_approximate_count_triangles.pdf)
- Also clustering coefficients in social networks: https://cs.stanford.edu/~rishig/courses/ref/l1.pdf
Enumerate explicitly over all triples and check which are triangles, using the adjacency matrix.
graph_matrix[][]

let mut count: u32 = 0;
let mut coefficients: Vec<u32> = vec![0;n];
for u in 0..n {
for v in u+1..n {
for w in v+1..n {
if (graph_matrix[u][v] && graph_matrix[v][w] && graph_matrix[w][u]) {
count += 1;
coefficients[u] += 1;
coefficients[v] += 1;
coefficients[w] += 1;
}
}
}
}
println!("{}", count);
println!("{:?}", coefficients);
2
[2, 1, 2, 1, 0, 0]
Complexity of the algorithm above is
Why?
hint: look at the nested loops.
Follow links from each vertex to see if you come back in three steps, using adjacency list.
![[sample graph]](modules/images/sparse.png)
let mut count: u32 = 0;
for u in 0..n {
for v in &graph_list[u] { // v is the adjacency list for node u
for w in &graph_list[*v] { // w is the adjacency list for node v
for u2 in &graph_list[*w] { // now iterate through this 3rd list
if u == *u2 { // if we find the origin node, we closed the loop in 3 steps
count += 1;
break;
}
}
}
}
}
count
12
Now we need to account for duplicate counting.
For every triangle there are 2 different directions to traverse the same nodes.
For every triangle, we can start with one each of the 3 nodes to count.
// need to divide by 6
// due to symmetries triangles counted multiple times
count / (2*3)
2
Complexity
We have 4 nested loops, so worse case where every node is connected to every other node, we have complexity of .
In practice, nodes are connected more sparsely and the complexity can be shown to be , where is number of nodes and is number of edges.
Question: How did we avoid duplicate counting in the matrix version, Solution 1?
Different implementation of solution 2, using a recursive algorithm.
- Do a recursive walk through the graph and terminate after 3 steps.
- If I land where I started, then I found a triangle.
fn walk(current:usize, destination:usize, steps:usize, adjacency_list:&Vec<Vec<usize>>) -> u32 {
match steps {
0 => if current == destination {1} else {0},
_ => {
let mut count = 0;
for v in &adjacency_list[current] {
count += walk(*v,destination,steps-1,adjacency_list);
}
count
}
}
}
let mut count = 0;
for v in 0..n {
count += walk(v,v,3,&graph_list);
}
count / 6
2
For each vertex try all pairs of neighbors (via adjacency lists) and see if they are connected (via adjacency matrix).
let mut count: u32 = 0;
for u in 0..n {
let neighbors = &graph_list[u]; // get the adjacency list for node `u`
// now try all combinations of node pairs from that adjacency list
for v in neighbors {
for w in neighbors {
if graph_matrix[*v][*w] { // v,w are connected and both connected to u since they are in u's adjacency list
count += 1;
}
}
}
}
// again we duplicated counted
count / 6
2
Complexity Analysis
The code is using both an adjacency list (graph_list) and an adjacency matrix (graph_matrix) representation of the graph.
Let's break down the complexity:
- The outer loop iterates through all nodes
ufrom 0 to n-1: O(n) - For each node
u, it gets its adjacency listneighbors - For each node
vin the neighbors list, it iterates through all nodeswin the same neighbors list - For each pair (v,w), it checks if they are connected using the adjacency matrix: O(1)
The key insight is that for each node u, we're looking at all pairs of its neighbors. The number of pairs is proportional to the square of the degree of node u.
Let's denote:
- n = number of nodes
- m = number of edges
- d(u) = degree of node u
The complexity can be expressed as: Σ (d(u)²) for all nodes u
In the worst case, if the graph is complete (every node connected to every other node), each node has degree n-1, so the complexity would be O(n³).
However, in practice, most real-world graphs are sparse (m << n²). For sparse graphs, the average degree is much smaller than n. If we assume the average degree is d, then the complexity would be O(n * d²).
This is more efficient than the naive O(n³) approach of checking all possible triplets of nodes, but it's still quite expensive for dense graphs or graphs with high-degree nodes (hubs).
The final division by 6 is just a constant factor adjustment to account for counting each triangle 6 times (once for each permutation of the three nodes), so it doesn't affect the asymptotic complexity.
Graph Exploration and Search Algorithms
About This Module
This module introduces fundamental graph exploration techniques, focusing on breadth-first search (BFS) and depth-first search (DFS). Students will learn to represent graphs using adjacency lists, implement graph data structures in Rust, and understand the theoretical foundations of graph traversal algorithms. The module provides essential building blocks for more advanced graph algorithms and demonstrates practical applications in data science and network analysis.
Prework
Before this lecture, please read:
- The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
- The Rust Book Chapter 10.1: "Generic Data Types" - https://doc.rust-lang.org/book/ch10-01-syntax.html
- Introduction to Algorithms Chapter 22: "Elementary Graph Algorithms" (if available, or similar graph theory resource)
Pre-lecture Reflections
- What are the advantages and disadvantages of different graph representations (adjacency matrix vs. adjacency list)?
- How do BFS and DFS differ in their exploration patterns and use cases?
- What types of real-world problems can be modeled as graph traversal problems?
Lecture
Learning Objectives
By the end of this lecture, you should be able to:
- Represent graphs using adjacency lists in Rust
- Understand the difference between directed and undirected graphs
- Implement basic graph data structures with type aliases and structs
- Create utility functions for graph manipulation
- Identify appropriate graph representations for different problem types
Graph exploration overview
Graph exploration
Sample popular methods:
-
breadth–first search (BFS)
- uses a queue
-
depth–first search (DFS)
- uses a stack
-
random walks
- example: PageRank (see Homework 7)
BFS and DFS
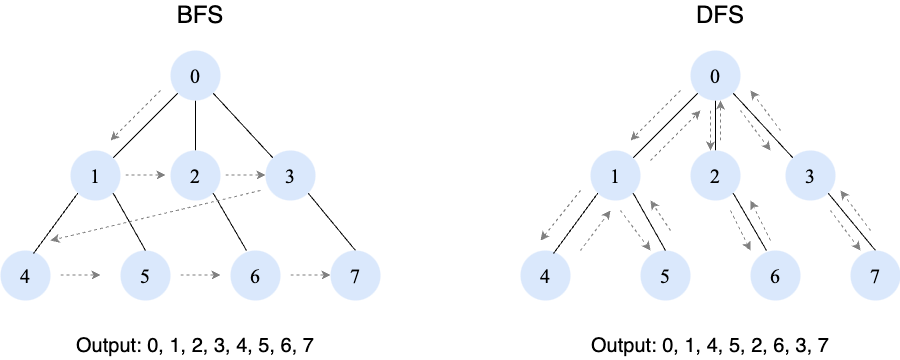
Useful graph subroutines
We'll start by defining some useful routines.
// Define some datatype synonyms
type Vertex = usize;
type ListOfEdges = Vec<(Vertex,Vertex)>;
type AdjacencyLists = Vec<Vec<Vertex>>;
#[derive(Debug)]
struct Graph {
n: usize, // vertex labels in {0,...,n-1}
outedges: AdjacencyLists,
}
// reverse direction of edges on a list
fn reverse_edges(list:&ListOfEdges)
-> ListOfEdges {
let mut new_list = vec![];
for (u,v) in list {
new_list.push((*v,*u));
}
new_list
}
reverse_edges(&vec![(3,2),(1,1),(0,100),(100,0)])
[(2, 3), (1, 1), (100, 0), (0, 100)]
impl Graph {
fn add_directed_edges(&mut self,
edges:&ListOfEdges) {
for (u,v) in edges {
self.outedges[*u].push(*v);
}
}
fn sort_graph_lists(&mut self) {
for l in self.outedges.iter_mut() {
l.sort();
}
}
fn create_directed(n:usize,edges:&ListOfEdges)
-> Graph {
let mut g = Graph{n,outedges:vec![vec![];n]};
g.add_directed_edges(edges);
g.sort_graph_lists();
g
}
fn create_undirected(n:usize,edges:&ListOfEdges)
-> Graph {
let mut g = Self::create_directed(n,edges);
g.add_directed_edges(&reverse_edges(edges));
g.sort_graph_lists();
g
}
}
Breadth-First Search (BFS) Algorithm
About This Module
This module provides an in-depth exploration of the breadth-first search (BFS) algorithm, a fundamental graph traversal technique. Students will learn to implement BFS in Rust, understand its computational complexity, and apply it to solve important graph problems such as shortest path finding and connected component detection. The module emphasizes both theoretical understanding and practical implementation skills.
Prework
Before this lecture, please read:
- Introduction to Algorithms Chapter 22.2: "Breadth-first search" (if available)
- The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
- Rust std::collections::VecDeque documentation - https://doc.rust-lang.org/std/collections/struct.VecDeque.html
Pre-lecture Reflections
- Why is BFS particularly useful for finding shortest paths in unweighted graphs?
- How does the queue data structure enable BFS's level-by-level exploration?
- What are some real-world applications where BFS would be the preferred search strategy?
Lecture
Learning Objectives
By the end of this lecture, you should be able to:
- Implement the BFS algorithm using queues and proper graph traversal techniques
- Analyze BFS's O(V+E) time complexity and understand why it achieves this bound
- Apply BFS to solve shortest path problems in unweighted graphs
- Use BFS for connected component detection in undirected graphs
- Trace through BFS execution and predict its behavior on different graph structures
Sample graph
![[first sample graph]](modules/images/graph_1_0.svg)
let n: usize = 10;
let mut edges: ListOfEdges = vec![(0,1),(0,2),(1,2),(2,4),(2,3),(4,3),(4,5),(5,6),(4,6),(6,8),(6,7),(8,7),(1,9)];
edges.sort();
println!("{:?}",edges);
let graph = Graph::create_undirected(n,&edges);
for (i, l) in graph.outedges.iter().enumerate() {
println!("{} {:?}", i, *l);
}
[(0, 1), (0, 2), (1, 2), (1, 9), (2, 3), (2, 4), (4, 3), (4, 5), (4, 6), (5, 6), (6, 7), (6, 8), (8, 7)]
0 [1, 2]
1 [0, 2, 9]
2 [0, 1, 3, 4]
3 [2, 4]
4 [2, 3, 5, 6]
5 [4, 6]
6 [4, 5, 7, 8]
7 [6, 8]
8 [6, 7]
9 [1]
()
Breadth–first search (BFS)
General idea:
- start from some vertex and explore its neighbors (distance 1)
- then explore neighbors of neighbors (distance 2)
- then explore neighbors of neighbors of neighbors (distance 3)
- ...
Our example: start from vertex 2
![[first sample graph]](modules/images/graph_1_1.svg)
Whiteboard walk-through
Let's first walk through the process interactively, then look at the code implementaiton.
The following reorganizes the graph to group by number of steps from the starting node.
![[first sample graph, grouped into layers]](modules/images/graph_1_2.svg)
Implementation: compute distances from vertex 2 via BFS -- I
distance[v]: distance of v from vertex 2 (None is unknown)
let start: Vertex = 2; // <= we'll start from this vertex
let mut distance: Vec<Option<u32>> = vec![None;graph.n];
distance[start] = Some(0); // <= we know this distance
distance
[None, None, Some(0), None, None, None, None, None, None, None]
queue: vertices to consider, they will arrive layer by layer
use std::collections::VecDeque;
let mut queue: VecDeque<Vertex> = VecDeque::new();
queue.push_back(start);
queue
[2]
Implementation: compute distances from vertex 2 via BFS -- II
Main loop:
consider vertices one by one
add their new neighbors to the processing queue
println!("{:?}",queue);
while let Some(v) = queue.pop_front() { // new unprocessed vertex
println!("top {:?}",queue);
for u in graph.outedges[v].iter() {
if let None = distance[*u] { // consider all unprocessed neighbors of v
distance[*u] = Some(distance[v].unwrap() + 1);
queue.push_back(*u);
println!("In {:?}",queue);
}
}
};
[2]
top []
In [0]
In [0, 1]
In [0, 1, 3]
In [0, 1, 3, 4]
top [1, 3, 4]
top [3, 4]
In [3, 4, 9]
top [4, 9]
top [9]
In [9, 5]
In [9, 5, 6]
top [5, 6]
top [6]
top []
In [7]
In [7, 8]
top [8]
top []
Implementation: compute distances from vertex 2 via BFS -- III
Compare results:
![[layers]](modules/images/graph_1_2.svg)
print!("vertex:distance");
for v in 0..graph.n {
print!(" {}:{}",v,distance[v].unwrap());
}
println!();
vertex:distance 0:1 1:1 2:0 3:1 4:1 5:2 6:2 7:3 8:3 9:2
What if we wanted the distance from all to all?
// let's wrap the previous code in a function
fn compute_and_print_distance_bfs(start: Vertex, graph: &Graph) {
let mut distance: Vec<Option<u32>> = vec![None;graph.n];
distance[start] = Some(0); // <= we know this distance
let mut queue: VecDeque<Vertex> = VecDeque::new();
queue.push_back(start);
while let Some(v) = queue.pop_front() { // new unprocessed vertex
for u in graph.outedges[v].iter() {
if let None = distance[*u] { // consider all unprocessed neighbors of v
distance[*u] = Some(distance[v].unwrap() + 1);
queue.push_back(*u);
}
}
}
print!("vertex:distance");
for v in 0..graph.n {
print!(" {}:{}",v,distance[v].unwrap());
}
println!();
}
// Then loop to start BFS from each node
for i in 0..graph.n {
println!("Distances from node {}", i);
compute_and_print_distance_bfs(i, &graph);
}
Distances from node 0
vertex:distance 0:0 1:1 2:1 3:2 4:2 5:3 6:3 7:4 8:4 9:2
Distances from node 1
vertex:distance 0:1 1:0 2:1 3:2 4:2 5:3 6:3 7:4 8:4 9:1
Distances from node 2
vertex:distance 0:1 1:1 2:0 3:1 4:1 5:2 6:2 7:3 8:3 9:2
Distances from node 3
vertex:distance 0:2 1:2 2:1 3:0 4:1 5:2 6:2 7:3 8:3 9:3
Distances from node 4
vertex:distance 0:2 1:2 2:1 3:1 4:0 5:1 6:1 7:2 8:2 9:3
Distances from node 5
vertex:distance 0:3 1:3 2:2 3:2 4:1 5:0 6:1 7:2 8:2 9:4
Distances from node 6
vertex:distance 0:3 1:3 2:2 3:2 4:1 5:1 6:0 7:1 8:1 9:4
Distances from node 7
vertex:distance 0:4 1:4 2:3 3:3 4:2 5:2 6:1 7:0 8:1 9:5
Distances from node 8
vertex:distance 0:4 1:4 2:3 3:3 4:2 5:2 6:1 7:1 8:0 9:5
Distances from node 9
vertex:distance 0:2 1:1 2:2 3:3 4:3 5:4 6:4 7:5 8:5 9:0
()
Computational complexity of BFS
O(V+E) where V is the number of vertices and E is the number of edges
Why?
Two loops:
- The outside loop goes through vertices and will go through every vertex and will only do so once!
- The inside loop goes through the edges of that vertex.
- But if you go through the edges of every vertex that is equal to the total number of edges. So it's not multiplicative but additive.
Strength of BFS
So we see one strength of BFS is that it is good at calculating distances.
Connected components via BFS
Connected component (in an undirected graph):
![[second graph]](modules/images/graph_2.svg)
Sample graph:
let n: usize = 9;
let edges: Vec<(Vertex,Vertex)> = vec![(0,1),(0,2),(1,2),(2,4),(0,4),(5,7),(6,8)];
let graph = Graph::create_undirected(n, &edges);
Discovering vertices of a connected component via BFS
component[v]: v's component's number (Nonenot assigned yet)
type Component = usize;
/*
* Loop through all the vertices connected to the passed in vertex and assign it the same
* component group number.
*/
fn mark_component_bfs(vertex:Vertex, // current vertex number
graph:&Graph, // graph structure
component:&mut Vec<Option<Component>>, // the component assignment for each node
component_no:Component // the component group of the current vertex
) {
component[vertex] = Some(component_no);
let mut queue = std::collections::VecDeque::new();
queue.push_back(vertex);
while let Some(v) = queue.pop_front() {
for w in graph.outedges[v].iter() {
if let None = component[*w] { // if node not assigned to a component group yet
component[*w] = Some(component_no); // assign it the current component number
queue.push_back(*w); // push it onto the queue to search since it is connected
}
}
}
}
Marking all connected components
Loop over all unassigned vertices and assign component numbers
// Vec of component assignments for each node, initialized to None
let mut component: Vec<Option<Component>> = vec![None;n];
let mut component_count = 0;
for v in 0..n {
if let None = component[v] {
component_count += 1;
mark_component_bfs(v, &graph, &mut component, component_count);
}
};
// Let's verify the assignment!
print!("{} components:\n[ ",component_count);
for v in 0..n {
print!("{}:{} ",v,component[v].unwrap());
}
println!("]\n");
4 components:
[ 0:1 1:1 2:1 3:2 4:1 5:3 6:4 7:3 8:4 ]
![[components]](modules/images/graph_2.svg)
Question: What is complexity of this algorithm?
It is also .
Depth-First Search (DFS) Algorithm
About This Module
This module covers the depth-first search (DFS) algorithm, a fundamental graph traversal technique that explores as far as possible along each branch before backtracking. Students will learn to implement DFS in Rust, understand its applications in topological sorting and strongly connected components, and compare it with BFS. The module emphasizes both recursive and iterative implementations while exploring DFS's unique strengths in graph analysis.
Prework
Before this lecture, please read:
- Introduction to Algorithms Chapter 22.3: "Depth-first search" (if available)
- The Rust Book Chapter 6.1: "Defining and Instantiating Structs" - https://doc.rust-lang.org/book/ch06-01-defining-structs.html
- The Rust Book Chapter 5.3: "Method Syntax" - https://doc.rust-lang.org/book/ch05-03-method-syntax.html
Pre-lecture Reflections
- How does DFS's exploration pattern differ from BFS, and when might this be advantageous?
- What are the advantages and challenges of implementing DFS recursively vs. iteratively?
- In what types of graph problems would DFS be preferred over BFS?
Lecture
Learning Objectives
By the end of this lecture, you should be able to:
- Implement DFS using both recursive and iterative approaches
- Understand DFS's applications in topological sorting and cycle detection
- Analyze the computational complexity and memory usage of DFS
- Apply DFS to find strongly connected components in directed graphs
- Compare DFS and BFS for different graph analysis tasks
DFS Example
Depth–First Search (DFS) -- I
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_1.svg)
Depth–First Search (DFS) -- II
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_2.svg)
Depth–First Search (DFS) -- III
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_3.svg)
Depth–First Search (DFS) -- IV
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_4.svg)
Depth–First Search (DFS) -- V
General idea:
- keep moving to an unvisited neighbor
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_5.svg)
Depth–First Search (DFS) -- VI
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_6.svg)
Depth–First Search (DFS) -- VII
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_7.svg)
Depth–First Search (DFS) -- VIII
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_8.svg)
Depth–First Search (DFS) -- IX
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_9.svg)
Depth–First Search (DFS) -- X
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_10.svg)
Depth–First Search (DFS) -- XI
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_11.svg)
Depth–First Search (DFS) -- XII
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_12.svg)
Depth–First Search (DFS) -- XIII
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_13.svg)
Depth–First Search (DFS) -- XIV
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_14.svg)
Depth–First Search (DFS) -- XV
General idea:
- keep going to an unvisited vertex
- when stuck make a step back and try again
![[dfs demo]](modules/images/graph_3_15.svg)
Our sample graph from BFS
![[first sample graph]](modules/images/graph_1_0.svg)
DFS Implementation
fn dfs(vertex:Vertex, // starting vertex
graph: &Graph, // graph structure
d: usize, // distance of node connected to passed in vertex
visited: &mut Vec<bool>, // Vec of bools indicating if we visited a node
distance: &mut Vec<usize> // Vec of distances of each vertex from the starting vertex
){
// loop through every vertex connected to the current vertex
for w in graph.outedges[vertex].iter() {
if visited[*w] == false {
distance[*w] = d;
visited[*w] = true;
dfs(*w, graph, d+1, visited, distance);
}
}
}
let n: usize = 10;
let edges: ListOfEdges = vec![(0,1),(0,2),(1,2),(2,4),(2,3),(4,3),(4,5),(5,6),(4,6),(6,8),(6,7),(8,7),(1,9)];
let graph = Graph::create_undirected(n,&edges);
let mut visited = vec![false;graph.n];
let mut distance = vec![0;graph.n];
visited[2] = true;
distance[2] = 0;
dfs(2, &graph, 1, &mut visited, &mut distance);
println!("vertex:distance");
for v in 0..graph.n {
print!(" {}:{}",v,distance[v]);
}
println!();
// For comparison this was the distance from bfs
// vertex:distance 0:1 1:1 2:0 3:1 4:1 5:2 6:2 7:3 8:3 9:2
vertex:distance
0:1 1:2 2:0 3:1 4:2 5:3 6:4 7:5 8:6 9:3Connected Components and Strongly Connected Components
About This Module
This module explores connected components in undirected graphs and strongly connected components in directed graphs. Students will learn advanced applications of DFS, including the two-pass algorithm for finding strongly connected components (Kosaraju's algorithm). The module covers both theoretical concepts and practical implementations, with applications to network analysis and graph decomposition problems.
Prework
Before this lecture, please read:
- Introduction to Algorithms Chapter 22.5: "Strongly connected components" (if available)
- The Rust Book Chapter 8.1: "Storing Lists of Values with Vectors" - https://doc.rust-lang.org/book/ch08-01-vectors.html
- Graph Theory reference on strongly connected components (any introductory graph theory text)
Pre-lecture Reflections
- What is the difference between connected components and strongly connected components?
- Why do we need different algorithms for directed vs. undirected graphs?
- How might strongly connected components be useful in analyzing real-world networks?
Lecture
Learning Objectives
By the end of this lecture, you should be able to:
- Understand the difference between connected and strongly connected components
- Implement connected component detection using both BFS and DFS
- Apply Kosaraju's algorithm to find strongly connected components
- Analyze the computational complexity of component detection algorithms
- Apply component analysis to real-world graph problems
Connected components via DFS
Recursive DFS exploration: walk all connected vertices depth-first rather than breadth-first
fn mark_component_dfs(vertex:Vertex, graph:&Graph, component:&mut Vec<Option<Component>>, component_no:Component) {
component[vertex] = Some(component_no);
for w in graph.outedges[vertex].iter() {
if let None = component[*w] {
mark_component_dfs(*w,graph,component,component_no);
}
}
}
Going over all components and assigning vertices:
let n: usize = 9;
let edges: Vec<(Vertex,Vertex)> = vec![(0,1),(0,2),(1,2),(2,4),(0,4),(5,7),(6,8)];
let graph = Graph::create_undirected(n, &edges);
let mut component = vec![None;graph.n];
let mut component_count = 0;
for v in 0..graph.n {
if let None = component[v] {
component_count += 1;
mark_component_dfs(v,&graph,&mut component,component_count);
}
};
Connected components via DFS
Let's verify the results:
print!("{} components:\n[ ",component_count);
for v in 0..n {
print!("{}:{} ",v,component[v].unwrap());
}
println!("]\n");
4 components:
[ 0:1 1:1 2:1 3:2 4:1 5:3 6:4 7:3 8:4 ]
![[components]](modules/images/graph_2.svg)
Takeaway: Works just as well as BFS for finding connected components.
BFS vs. DFS
Both have complexity of
BFS
- gives graph distances between vertices (fundamental problem!)
- connectivity
DFS
- What is it good for?
Lots of things!
Examples:
- find edges/vertices crucial for connectivity
- orient edges of a graph so it is still connected
- strongly connected components in directed graphs
- Traversal of trees (inorder, preorder, postorder)
- Topological Sorting (Scheduling)
- Matching people and jobs
Topological sort (pseudocode for home study)
Represents an order of the nodes that respects dependencies from directed graphs.
Assume this is a graph of dependent tasks.
Used whenever you have to schedule work only after satisfying dependencies.
Used in Neural Network Backpropagation.
Valid topo sorts:
- 0, 1, 3, 2
- 0, 3, 1, 2
- 3, 0, 1, 2
Invalid topo sorts:
- 0, 1, 2, 3
- 1, 3, 0, 2
- ...
Pseudocode (For study at home)
Every node can have one of three marks:
- unmarked: initial state
- temporary mark: being processed
- permanent mark: fully processed
In the beginngin all nodes are unmarked.
Pick an unmarked node and call visit() on that node.
L ← Empty list that will contain a valid order of nodes
while exists nodes without a permanent mark do
select an unmarked node n
visit(n)
function visit(node n)
if n has a permanent mark then
return
if n has a temporary mark then
stop (graph has at least one cycle -- can't be sorted)
mark n with a temporary mark
for each node m with an edge from n to m do
visit(m)
remove temporary mark from n
mark n with a permanent mark
add n to head of L
Complexith of topological sort
Complexity is . Just doing a DFS.
Strongly connected components (for directed graphs)
Only applies to directed graphs.
Strong connectivity
What if you can get from to , but not from to ?
Strongly connected component:
A maximal set of vertices such that you can get from any of them to any other one. So like connected components but taking directionality into account
Strongly connected: nodes 0, 1, 2
Strongly connected: nodes, 3, 4, 5
Fact: There is a unique decomposition
Find the unique decomposition via two DFS runs
General idea
First DFS:
- maintain auxiliary stack
- visit all vertices, starting DFS multiple times from unvisited vertices as needed
- put each vertex, when done going over its neighbors, on the stack
Second DFS:
- reverse edges of the graph!!!
- consider vertices in order from the stack
- for each unvisited vertex, start DFS: it will visit a new strongly connected component
Implementation

let n: usize = 7;
let edges: ListOfEdges = vec![(0,1),(1,2),(2,0),(3,4),(4,5),(5,3),(2,3),(6,5)];
let graph = Graph::create_directed(n, &edges);
let graph_reverse = Graph::create_directed(n,&reverse_edges(&edges));
println!("{:?}\n{:?}",graph,graph_reverse);
Graph { n: 7, outedges: [[1], [2], [0, 3], [4], [5], [3], [5]] }
Graph { n: 7, outedges: [[2], [0], [1], [2, 5], [3], [4, 6], []] }
Implementation (first DFS)
let mut stack: Vec<Vertex> = Vec::new();
let mut visited = vec![false;graph.n];
// push vertex onto stack after all descendents are processed (a.k.a. finishing times)
fn dfs_collect_stack(v:Vertex, graph:&Graph, stack:&mut Vec<Vertex>, visited:&mut Vec<bool>) {
if !visited[v] {
visited[v] = true;
for w in graph.outedges[v].iter() {
dfs_collect_stack(*w, graph, stack, visited);
}
stack.push(v);
println!("pushed {}", v);
}
}
for v in 0..graph.n {
dfs_collect_stack(v,&graph,&mut stack,&mut visited);
};
stack
pushed 5
pushed 4
pushed 3
pushed 2
pushed 1
pushed 0
pushed 6
[5, 4, 3, 2, 1, 0, 6]
Implementation (second DFS, reversed graph)
let mut component: Vec<Option<Component>> = vec![None;graph.n];
let mut component_count = 0;
while let Some(v) = stack.pop() {
if let None = component[v] {
component_count += 1;
mark_component_dfs(v, &graph_reverse, &mut component, component_count);
}
};
print!("{} components:\n",component_count);
for c in 1..=component_count {
print!("Component {}: ", c);
for v in 0..n {
if component[v].unwrap() == c {
print!("{} ",v);
}
}
println!();
}
println!();
3 components:
Component 1: 6
Component 2: 0 1 2
Component 3: 3 4 5
Rust project version
Rust project version in strongly_connected folder in case you want to debug and inspect.
Code Formatting and Rust Best Practices
About This Module
This module focuses on code formatting, readability, and best practices in Rust programming. Students will learn about the importance of clean, readable code and how to use Rust's built-in formatting tools. The module covers rustfmt, code style guidelines, and techniques for writing maintainable code that follows Rust community standards.
Prework
Before this lecture, please read:
- The Rust Book Chapter 1.3: "Hello, Cargo!" - https://doc.rust-lang.org/book/ch01-03-hello-cargo.html
- The rustfmt book - https://rust-lang.github.io/rustfmt/
- Rust API Guidelines - https://rust-lang.github.io/api-guidelines/ (introduction sections)
Pre-lecture Reflections
- Why is consistent code formatting important in team development?
- How might automated formatting tools improve code quality and developer productivity?
- What are some examples of code that is technically correct but difficult to read?
Lecture
Learning Objectives
By the end of this lecture, you should be able to:
- Use
rustfmtto automatically format Rust code - Understand Rust community style conventions
- Write readable and maintainable code
- Apply refactoring techniques to improve code clarity
- Configure and customize formatting tools for your development workflow
Don't give up on code formatting!
- Rust doesn't require any specific indentation
- Still a good idea to make your code readable
//This is bad code
fn h(z:i32)->i32{
let mut t=0.max(z.min(1)-0.max(z-1));
for y in 1..=2.min(z){
t+=h(z-y)
}
t
}
//This is even worse code
fn g(z:i32)->i32{let mut t=0.max(z.min(1)-0.max(z-1));for y in 1..=2.min(z){t+=g(z-y)}t}
// This is good code
fn f(z:i32)->i32 {
let t;
if z==0{
t = 0;
} else if z == 1 {
t = 1;
} else {
t = f(z-1) + f (z-2);
}
t
}
for i in 0..10 {
println!("{}:{},{},{}",i,h(i),g(i),f(i));
};
0:0,0,0
1:1,1,1
2:1,1,1
3:2,2,2
4:3,3,3
5:5,5,5
6:8,8,8
7:13,13,13
8:21,21,21
9:34,34,34
Tool for formatting Rust code: rustfmt
-
If you have Rust installed, you should already have it.
-
rustfmt [filename]replaces the file with nicely formatted version- use
rustfmt --backup [filename]to save the original file
- use
-
rustfmt --help: see the command line parameters -
rustfmt --print-config default: default config that can be adjusted
Other style tips:
- If you repeat sections of code, move it to a function
- If you have many if, else if, ... --> move it to a match statement
- if the body of a match variant is large, move content to a function...
- ...
Priority Queues in Rust
About This Module
This module introduces priority queues, a fundamental data structure that serves elements based on their priority rather than insertion order. We'll explore Rust's BinaryHeap implementation, custom ordering with structs, and analyze the time complexity of various priority queue operations.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
- Chapter 8.1: Storing Lists of Values with Vectors
- Chapter 10.2: Traits
- Collections documentation for BinaryHeap
Pre-lecture Reflections
Before class, consider these questions:
- How do priority queues differ from regular FIFO queues in their use cases?
- What are some real-world applications where priority-based ordering is essential?
- How does the Ord trait enable custom priority ordering in Rust?
- What trade-offs exist between different priority queue implementations?
- When would you choose a priority queue over sorting all elements at once?
Lecture
Learning Objectives
By the end of this module, you should be able to:
- Understand the difference between standard queues and priority queues
- Use Rust's BinaryHeap for priority queue operations
- Implement custom ordering with structs using derive and manual trait implementation
- Apply the Reverse wrapper to change ordering behavior
- Analyze time complexity of priority queue operations
- Design priority-based systems for real-world applications
Priority Queues
Standard queue:
- things returned in order in which they were inserted
Priority queue:
- items have priorities
- highest priority items returned first
Example of Priority Queue
Triage in a hospital emergency room.
For non-critical injuries, perhaps FIFO, but heart attack gets priority.
Rust standard library implementation: BinaryHeap<T>
- Priorities provided by the ordering of elements of
T(via traitOrd)
- Method
push(T):
push element onto the heap
- Method
pop() -> Option<T>:
remove the greatest and return it Some(T) or None
use std::collections::BinaryHeap;
let mut pq = BinaryHeap::new();
pq.push(2);
pq.push(7);
pq.push(3);
println!("{:?}",pq.pop());
println!("{:?}",pq.pop());
pq.push(3);
pq.push(4);
println!("\n{:?}",pq.pop());
println!("{:?}",pq.pop());
println!("{:?}",pq.pop());
println!("{:?}",pq.pop());
Some(7)
Some(3)
Some(4)
Some(3)
Some(2)
None
You can use more complex data types, like your own structs with a priority field, then you have to implement your own Ord trait.
Getting the smallest element out first
Reverse<T>: wrapper that reverses the ordering of elements of a type
3 < 4
true
use std::cmp::Reverse;
Reverse(3) < Reverse(4)
false
5 < 3
false
Reverse(5) < Reverse(3)
true
let mut pq = BinaryHeap::new();
pq.push(Reverse(3));
pq.push(Reverse(1));
pq.push(Reverse(7));
println!("{:?}",pq.pop());
println!("{:?}",pq.pop());
pq.push(Reverse(0));
println!("\n{:?}",pq.pop());
println!("\n{:?}",pq.pop());
println!("\n{:?}",pq.pop());
Some(Reverse(1))
Some(Reverse(3))
Some(Reverse(0))
Some(Reverse(7))
None
How to extract inner value from Reverse()
// Method 1: Using .0 to access the inner value (since Reverse is a tuple struct)
let rev = Reverse(3);
let value = rev.0; // value = 3
println!("{value}");
// Method 2: Using pattern matching
let rev = Reverse(5);
let Reverse(value) = rev; // value = 5
println!("{value}");
3
5
Default lexicographic ordering on tuples and structs
Lexicographic ordering:
- Compare first elements
- If equal, compare second elements
- If equal, compare third elements...
Tuples
(3,4) < (2,7)
false
(11,2,7) < (11,3,4)
true
Struct (derive Ord)
A custom struct does not support lexicographic ordering, but we can derive traits.
#[derive(PartialEq,Eq,PartialOrd,Ord,Debug)]
struct Point {
x: i32,
y: i32,
}
let p = Point{x:3,y:4};
let q = Point{x:2,y:7};
println!("{}", p < q);
println!("{}", p > q);
false
true
let p = Point{x:3,y:4};
let q = Point{x:3,y:7};
println!("{}", p < q);
println!("{}", p > q);
true
false
Another option: implement your own comparison
-
More complicated, see below
-
See the documentation for
Ordor examples online
#[derive(PartialEq,Eq,Ord,Debug)]
struct Point2 {
x: i32,
y: i32,
}
// Let's assume we want to compare point by their distance to the origin
impl std::cmp::PartialOrd for Point2 {
fn partial_cmp(&self, other: &Self) -> Option<std::cmp::Ordering> {
// 'Self' (capital) is a shorthand for type Point2
let this = self.x * self.x + self.y * self.y;
let that = other.x * other.x + other.y * other.y;
return this.partial_cmp(&that); // use the partial_cmp() on integer
}
}
let p = Point2{x:3,y:1};
let q = Point2{x:2,y:100};
println!("{}", p < q);
println!("{}", p > q);
true
false
Complexity of a priority queue?
Assumptions:
- At most elements
- Comparison takes time
Straightforward
Representation: a vector of elements
Push:
- add to the end of the vector
- Time complexity: (amortized) time
Pop:
- go over all elements, select the greatest
- Time complexity:
Binary Heap Implementation
About This Module
This module explores the binary heap data structure, which is the foundation of efficient priority queue implementations. We'll examine the binary heap's tree structure, array-based storage, and implement core operations like push and pop with O(log n) complexity.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
- Chapter 8.1: Storing Lists of Values with Vectors
- Chapter 10.1: Generic Data Types
- Chapter 10.2: Traits: Defining Shared Behavior
Pre-lecture Reflections
Before class, consider these questions:
- Why is the binary heap structure optimal for priority queue operations?
- How does the complete binary tree property enable efficient array-based storage?
- What are the key invariants that must be maintained in a max heap?
- How do the parent-child index relationships work in array representation?
- What are the trade-offs between binary heaps and other priority queue implementations?
Lecture
Learning Objectives
By the end of this module, you should be able to:
- Understand the binary heap structure and its key properties
- Navigate binary heap using array indices for parent and child nodes
- Implement heapify operations to maintain heap ordering
- Build push and pop operations with O(log n) complexity
- Analyze the relationship between tree height and operation complexity
- Compare custom implementations with Rust's standard library BinaryHeap
Popular implementation: binary heap
Binary heaps
- Data organized into a binary tree (one root, each node with 0, 1 or 2 children)
- Every internal node not smaller (or greater) than its children
- Every layer is filled before the next layer starts
Basic property:
The root has the current maximum (minimum), i.e., the answer to next pop
![[picture of basic binary heap with heap ordering]](modules/images/order.png)
Heap storage properties
Efficient storage:
-
Tree levels filled from left to right
-
Can be mapped to a vector
-
Easy to move to the parent or children using vector indices
![[picture of basic binary heap with heap ordering]](modules/images/layers.png)
![[picture of basic binary heap with heap ordering]](modules/images/indices.png)
How are operations implemented?
Push
- add at the end the vector
- fix the ordering by swapping with the parent if needed
Pop
- remove and return the root
- replace with the last element
- fix the ordering by comparing with children and swapping with each that is greater
Complexity of push and pop
-
Proportional to the number of levels
-
So
Implementation
Utility methods
#![allow(unused)] fn main() { #[derive(Debug)] struct MyBinaryHeap<T> { heap: Vec<T>, heap_size: usize, } impl<T> MyBinaryHeap<T> { fn new() -> MyBinaryHeap<T> { let heap: Vec<T> = vec![]; let heap_size = 0; MyBinaryHeap { heap, heap_size } } // left child fn left(i: usize) -> usize { 2 * i + 1 } // right child of node i fn right(i: usize) -> usize { 2 * i + 2 } //parent of node i fn parent(i: usize) -> usize { (i - 1) / 2 // integer divide } } }
Heapify -- Put everything in proper order
Make it so children are parents.
#![allow(unused)] fn main() { impl<T:PartialOrd+PartialEq+Copy> MyBinaryHeap<T> { fn heapify(&mut self, loc: usize) { let l = Self::left(loc); let r: usize = Self::right(loc); let mut largest = loc; // index of largest if l < self.heap_size && self.heap[l] > self.heap[largest] { largest = l; } if r < self.heap_size && self.heap[r] > self.heap[largest] { largest = r; } if largest != loc { // swap with child let tmp = self.heap[loc]; self.heap[loc] = self.heap[largest]; self.heap[largest] = tmp; self.heapify(largest); } } } }
Insert and Extract
#![allow(unused)] fn main() { impl<T:PartialOrd+PartialEq+Copy> MyBinaryHeap<T> { fn insert_val(&mut self, val: T) { self.heap_size += 1; self.heap.push(val); let mut i = self.heap_size - 1; // loop until we reach root and parent is less than current node while i != 0 && self.heap[Self::parent(i)] < self.heap[i] { // swap node with parent let tmp = self.heap[Self::parent(i)]; self.heap[Self::parent(i)] = self.heap[i]; self.heap[i] = tmp; // update node number i = Self::parent(i); // Self is stand-in for data strucutre MyBinaryHeap } } fn extract_max(&mut self) -> Option<T> { if self.heap_size == 0 { return None; } if self.heap_size == 1 { self.heap_size -= 1; return Some(self.heap[0]); } let root = self.heap[0]; self.heap[0] = self.heap[self.heap_size - 1]; // copy last element self.heap_size -= 1; self.heapify(0); return Some(root); } } }
Let's run the code
#![allow(unused)] fn main() { :dep rand="0.8.5" use rand::Rng; let mut h:MyBinaryHeap::<i32> = MyBinaryHeap::new(); // Generate 10 random numberrs between -1000 and 1000 and insert for _i in 0..10 { let x = rand::thread_rng().gen_range(-1000..1000) as i32; h.insert_val(x); } println!("Print the BinaryHeap structure."); println!("{:?}", h); println!("\nExtract max values."); let size = h.heap_size; for _j in 0..size { let z = h.extract_max().unwrap(); print!("{} ", z); } println!("\n\nPrint what's left of the BinaryHeap structure"); println!("{:?}", h); }
Print the BinaryHeap structure.
MyBinaryHeap { heap: [983, 827, 654, 135, 757, -686, 191, -822, -349, 263], heap_size: 10 }
Extract max values.
983 827 757 654 263 191 135 -349 -686 -822
Print what's left of the BinaryHeap structure
MyBinaryHeap { heap: [-822, -822, -686, -822, -349, -686, -822, -822, -349, 263], heap_size: 0 }
Note: the last debug print shouldn't display values with heap_size: 0.
What is the property of the list of values we extracted?
Or use the built in one from std::collections
#![allow(unused)] fn main() { use std::collections::BinaryHeap; let mut heap = BinaryHeap::new(); heap.push(5); heap.push(2); heap.push(8); while let Some(max) = heap.pop() { println!("{}", max); } // Outputs: 8, 5, 2 }
The values are extracted in sorted order (largest first)!
Priority Queue Applications: Heap Sort and Dijkstra's Algorithm
About This Module
This module explores two major applications of priority queues: heap sort for efficient sorting and Dijkstra's algorithm for finding shortest paths in weighted graphs. We'll implement both algorithms using Rust's BinaryHeap and analyze their performance characteristics.
Prework
Prework Reading
Read the following sections from "The Rust Programming Language" book:
- Chapter 8.1: Storing Lists of Values with Vectors
- Chapter 8.3: Storing Keys with Associated Values in Hash Maps
- Review BinaryHeap documentation and priority queue concepts
Pre-lecture Reflections
Before class, consider these questions:
- How does heap sort compare to other O(n log n) sorting algorithms in terms of space complexity?
- Why is Dijkstra's algorithm considered a greedy algorithm, and when does this approach work?
- What are the limitations of Dijkstra's algorithm with negative edge weights?
- How do priority queues enable efficient implementation of graph algorithms?
- What are the trade-offs between different shortest path algorithms?
Lecture
Learning Objectives
By the end of this module, you should be able to:
- Implement heap sort using priority queues and analyze its complexity
- Understand and implement Dijkstra's shortest path algorithm
- Use Rust's BinaryHeap for efficient priority-based operations
- Compare heap sort with other sorting algorithms
- Design graph representations suitable for shortest path algorithms
- Analyze time and space complexity of priority queue applications
Application 1: Sorting a.k.a. HeapSort
- Put everything into a priority queue
- Remove items in order
#![allow(unused)] fn main() { use std::collections::BinaryHeap; fn heap_sort(v:&mut Vec<i32>) { let mut pq = BinaryHeap::new(); for v in v.iter() { pq.push(*v); } // to sort smallest to largest we iterate in reverse for i in (0..v.len()).rev() { v[i] = pq.pop().unwrap(); } } }
#![allow(unused)] fn main() { let mut v = vec![23,12,-11,-9,7,37,14,11]; heap_sort(&mut v); v }
[-11, -9, 7, 11, 12, 14, 23, 37]
Total running time: for numbers
More direct, using Rust operations
#![allow(unused)] fn main() { fn heap_sort_2(v:Vec<i32>) -> Vec<i32> { BinaryHeap::from(v).into_sorted_vec() } }
No extra memory allocated: the initial vector, intermediate binary heap, and final vector all use the same space on the heap
BinaryHeap::from(v)consumesvinto_sorted_vec()consumes the intermediate binary heap
#![allow(unused)] fn main() { let mut v = vec![7,17,3,1,8,11]; heap_sort_2(v) }
[1, 3, 7, 8, 11, 17]
Sorting already provided for vectors (currently use other algorithms): sort and sort_unstable
HeapSort is faster in time, but takes twice the memory.
#![allow(unused)] fn main() { let mut v = vec![7,17,3,1,8,11]; v.sort(); v }
[1, 3, 7, 8, 11, 17]
#![allow(unused)] fn main() { let mut v = vec![7,17,3,1,8,11]; v.sort_unstable(); // doesn't preserve order for equal elements v }
[1, 3, 7, 8, 11, 17]
Application 2: Shortest weighted paths (Dijkstra's algorithm)
- Input graph: edges with positive values, directed or undirected
- Edge is now (starting node, ending node, cost)
- Goal: Compute all distances from a given vertex
Some quotes from Edsger Dijkstra
Pioneer in computer science. Very opinionated.
The use of COBOL cripples the mind; its teaching should, therefore, be regarded as a criminal offence.
It is practically impossible to teach good programming to students that have had a prior exposure to BASIC: as potential programmers they are mentally mutilated beyond hope of regeneration.
One morning I was shopping in Amsterdam with my young fiancée, and tired, we sat down on the café terrace to drink a cup of coffee and I was just thinking... Eventually, that algorithm became to my great amazement, one of the cornerstones of my fame
Shortest Weighted Path Description
-
Mark all nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
-
Assign to every node a tentative distance value:
- set it to zero for our initial node and to infinity for all other nodes.
- During the run of the algorithm, the tentative distance of a node v is the length of the shortest path discovered so far between the node v and the starting node.
- Since initially no path is known to any other vertex than the source itself (which is a path of length zero), all other tentative distances are initially set to infinity.
- Set the initial node as current.
-
For the current node, consider all of its unvisited neighbors and calculate their tentative distances through the current node.
- Compare the newly calculated tentative distance to the one currently assigned to the neighbor and assign it the smaller one.
- For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B through A will be 6 + 2 = 8.
- If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, the current value will be kept.
-
When we are done considering all of the unvisited neighbors of the current node, mark the current node as visited and remove it from the unvisited set.
- A visited node will never be checked again
- (this is valid and optimal in connection with the behavior in step 6.: that the next nodes to visit will always be in the order of 'smallest distance from initial node first' so any visits after would have a greater distance).
-
If all nodes have been marked visited or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
-
Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new current node, and go back to step 3.
How it works:
-
Greedily take the closest unprocessed vertex
- Its distance must be correct
-
Keep updating distances of unprocessed vertices
Example
Let's illustrate by way of example: Directed graph with weighted edges.
Pick 0 as a starting node and assign it's distance as 0.
Assign distance of to all other nodes.
From 0, travel to each connected node and update the tentative distances.
Now go to the "closest" node (node 2) and update the distances to its immediate neighbors.
Mark node 2 as visited.

Randomly pick between nodes 4 and 1 since they both have updated distances 3.
Pick node 1.
Update the distances to it's nearest neighbors.
Mark node 1 as visited.
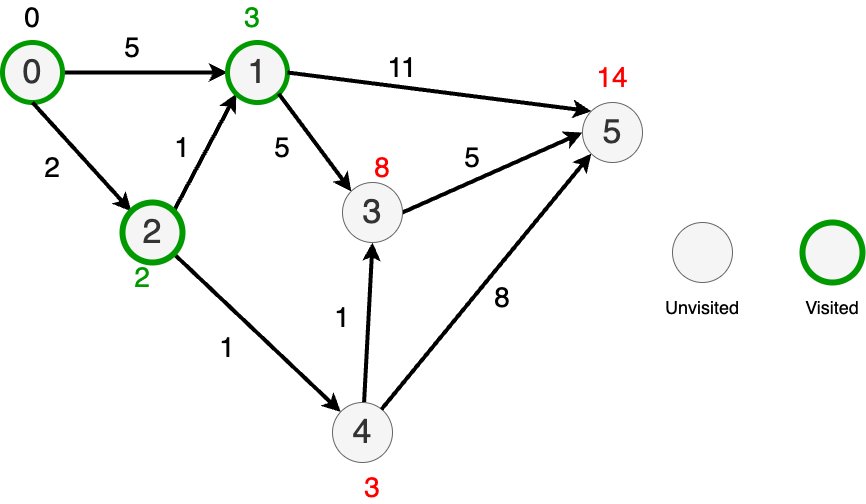
Now, pick the node with the lost distance (node 4) and update the distances to it's nearest neighbors.
Distances to nodes 3 and 4 improved.

Then, go to node 3 and update its distance to its nearest neighbor.
Nowhere else to go so mark everything as done.
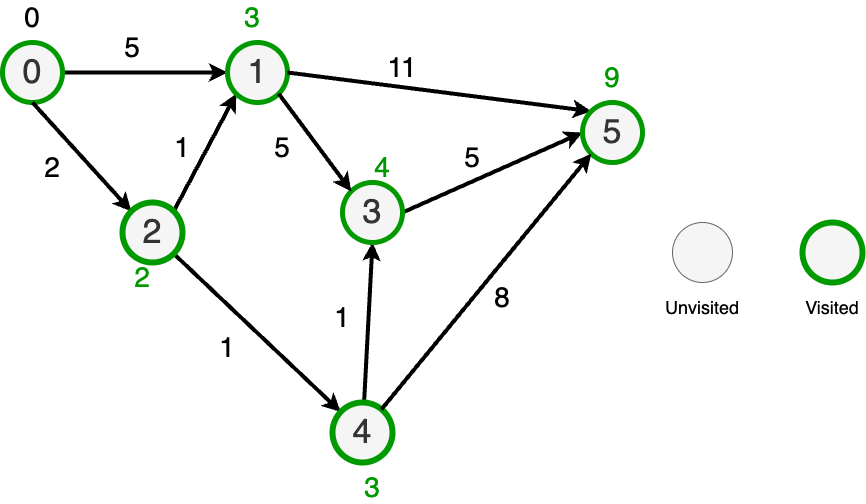
BinaryHeap to the rescue
Since we always want to pick the cheapest node, we can use a BinaryHeap to find the next node to check.
Dijkstra's Shortest Path Implementation
Auxiliary graph definitions
#![allow(unused)] fn main() { use std::collections::BinaryHeap; type Vertex = usize; type Distance = usize; type Edge = (Vertex, Vertex, Distance); // Updated edge definition. #[derive(Debug,Copy,Clone)] struct Outedge { vertex: Vertex, length: Distance, } type AdjacencyList = Vec<Outedge>; // Adjacency list of Outedge's #[derive(Debug)] struct Graph { n: usize, outedges: Vec<AdjacencyList>, } impl Graph { fn create_directed(n:usize,edges:&Vec<Edge>) -> Graph { let mut outedges = vec![vec![];n]; for (u, v, length) in edges { outedges[*u].push(Outedge{vertex: *v, length: *length}); // } Graph{n,outedges} } } }
Load our graph
#![allow(unused)] fn main() { let n = 6; let edges: Vec<Edge> = vec![(0,1,5),(0,2,2),(2,1,1),(2,4,1),(1,3,5),(4,3,1),(1,5,11),(3,5,5),(4,5,8)]; let graph = Graph::create_directed(n, &edges); graph }
Graph { n: 6, outedges: [[Outedge { vertex: 1, length: 5 }, Outedge { vertex: 2, length: 2 }], [Outedge { vertex: 3, length: 5 }, Outedge { vertex: 5, length: 11 }], [Outedge { vertex: 1, length: 1 }, Outedge { vertex: 4, length: 1 }], [Outedge { vertex: 5, length: 5 }], [Outedge { vertex: 3, length: 1 }, Outedge { vertex: 5, length: 8 }], []] }
Our implementation
#![allow(unused)] fn main() { let start: Vertex = 0; let mut distances: Vec<Option<Distance> > = vec![None; graph.n]; // use None instead of infinity distances[start] = Some(0); }
#![allow(unused)] fn main() { use core::cmp::Reverse; let mut pq = BinaryHeap::<Reverse<(Distance,Vertex)>>::new(); // make a min-heap with Reverse pq.push(Reverse((0,start))); }
#![allow(unused)] fn main() { // loop while we can pop -- deconstruct while let Some(Reverse((dist,v))) = pq.pop() { // boolean, not assignment for Outedge{vertex,length} in graph.outedges[v].iter() { let new_dist = dist + *length; let update = match distances[*vertex] { // assignment match None => {true} Some(d) => {new_dist < d} }; // update the distance of the node if update { distances[*vertex] = Some(new_dist); // record the new distance pq.push(Reverse((new_dist,*vertex))); } } }; }
#![allow(unused)] fn main() { distances }
[Some(0), Some(3), Some(2), Some(4), Some(3), Some(9)]
Complexity and properties of Dijkstra's algorithm
- -- worst case visit (N-1) nodes on every node
- Works just as well with undirected graphs
- Doesn't work if path weights can be negative (why?)
Traveling salesman
On the surface similar to shortest paths
Given an undirected graph with weighted non-negative edges find the shortest path that starts at a specified vertex, traverses every vertex in the graph and returns to the starting point.
Applications:
- Amazon deliver route optimization
- Drilling holes in circuit boards -- minimize stepping motor travel.
BUT
Much harder to solve (will not cover here). Provably NP-complete (can not be solved in Polynomial time)
Held-Karp algorithm one of the best exact algorithms with complexity
Many heuristics that run fast but yield suboptimal results
Greedy Heuristic
Mark all nodes as unvisited. Use your starting node and pick the next node with shortest distance and visit it. DFS using minimum distance criteria until all nodes have been visited.
Minimum Spanning Tree Heuristic
https://en.wikipedia.org/wiki/Minimum_spanning_tree
Runs in time and guaranteed to be no more than 50% worse than the optimal.
Binary search
About This Module
This module introduces the binary search algorithm, a fundamental technique for efficiently finding elements in sorted collections. You'll learn how binary search works, its time complexity, and how to implement it in Rust. The module also covers practical applications of binary search and common pitfalls to avoid.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 3.2: Guessing Game - Focus on input handling and basic control flow
- Chapter 4.1: Ownership - Understand how Rust manages memory
- Chapter 4.2: References and Borrowing - Learn about references, mutable references, and borrowing rules
- Chapter 4.3: The Slice Type - Understand slices and how they relate to arrays and vectors
Pre-lecture Reflections
Before class, consider these questions:
- What is the time complexity of binary search, and how does it compare to linear search?
- How does Rust's ownership and borrowing system impact the implementation of algorithms like binary search?
- What are some common pitfalls when implementing binary search, and how can they be avoided?
- How can binary search be adapted for different data structures, such as linked lists or trees?
Lecture
Learning Objectives
By the end of this module, you will be able to:
- Understand the binary search algorithm and its time complexity
- Implement binary search in Rust
- Apply binary search to solve practical problems
- Recognize common pitfalls and edge cases in binary search implementations
Binary Search
Input: sorted array/vector v
Task: find if a specific element x appears in it
General strategy:
- maintain range
left..rightwithinvof wherexcould be - repeat:
- ask about the middle of the range
- if
xfound, celebrate - if the middle element
x, narrow search to the right half - otherwise, narrow search to the left half
Let's implement it!
Might be harder than you think!
Jon Bentley in "Programming pearls" claims that only 10% programmers succeed, even given unlimited amount of time
Ad:
- Great book if you are interested in programming and basic algorithms
- First edition mostly uses pseudocode
- 2nd edition focused on C++ (probably still great)
- very cheap if you want to buy second hand (< $10)
Let's implement it!
/// Employ binary search on a sorted vector to find a value
///
/// # Arguments
///
/// * data:&[i32] -- sorted array
///
/// # Returns
///
/// * Option<(usize, i32)> -- Tuple of index and value
fn present(mut data:&[i32], element:i32) -> Option<(usize,i32)> {
let (mut left, mut right) = (0, data.len());
// invariant: if element has not been found, it must be in data[left..right]
while left < right {
let middle = (left+right)/2;
if data[middle] == element {
return Some((middle, element));
} else if data[middle] > element {
right = middle - 1
} else {
left = middle + 1
}
}
None
}
let v = vec![-16,-4,0,2,4,12,32,48,48,111];
present(&v, 111)
Some((9, 111))
present(&v, 5)
None
present(&v, 1000)
None
present(&v, 32)
Some((6, 32))
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Binary trees
About This Module
This module introduces binary trees, a fundamental data structure in computer science. You'll learn about the properties of binary trees, different types of binary trees (such as binary search trees and heaps), and how to implement and traverse them in Rust. The module will also cover common operations on binary trees, including insertion, deletion, and searching.
Prework
Prework Reading
Please read the following sections from The Rust Programming Language Book:
- Chapter 3.2: Guessing Game - Focus on input handling and basic control flow
- Chapter 4.1: Ownership - Understand how Rust manages memory
- Chapter 4.2: References and Borrowing - Learn about references, mutable references, and borrowing rules
- Chapter 4.3: The Slice Type - Understand slices and how they relate to arrays and vectors
Pre-lecture Reflections
Before class, consider these questions:
- What are the key properties of binary trees that differentiate them from other tree structures?
- How do binary search trees maintain order, and what are the implications for search, insertion and deletion operations?
- What are the advantages and disadvantages of using binary trees compared to other data structures like arrays or linked lists?
- How does Rust's ownership and borrowing system impact the implementation of binary trees?
- What are some common applications of binary trees in computer science and software development?
Lecture
Learning Objectives
By the end of this module, you will be able to:
- Understand the structure and properties of binary trees
- Implement binary trees in Rust
- Perform common operations on binary trees, including insertion, deletion, and searching
- Traverse binary trees using different algorithms (e.g., in-order, pre-order, post-order)
- Recognize different types of binary trees (e.g., binary search trees, heaps) and their use cases
- Analyze the time and space complexity of binary tree operations
Trees vs Graphs
Trees are a special type of graph with a few key features
- Hierarchical structure with a root node
- Acyclic
- Parent and child nodes with well-defined ancestry (every node besides the root has only one parent)
- Only n-1 edges for n nodes
- May constrain the number of children (in a binary tree each parent can have at most two children)
A general tree:
![[non-binary tree example]](modules/images/tree-example.jpg)
![[binary tree example]](modules/images/binary-tree-example.jpg)
Why are trees useful?
✅ Anything with a hierarchical data structure (e.g., File systems, HTML DOM structure)
- File systems: Directories and files form a natural tree—folders contain subfolders and files, and this nesting forms a hierarchy.
- HTML DOM: The structure of a webpage is a tree where elements nest inside each other; the root is usually the
<html>tag.
🗜 Data compression (Huffman coding)
- Builds a binary tree where the most frequent characters are near the top and less frequent ones further down.
- Encoding: Each character gets a unique binary string based on its path from the root—shorter for frequent characters.
🧠 Compilers use syntax trees (Abstract Syntax Trees - ASTs)
- Represents code structure: A program’s nested expressions, blocks, and statements naturally form a tree.
- Compiler passes: Syntax trees are walked recursively for semantic checks, optimization, and code generation.
- In Rust: The Rust compiler (rustc) builds and transforms ASTs as part of its pipeline
🔡 Prefix trees (Tries) (discussed below)
- Spell checking and autocomplete: Fast prefix search to suggest or validate words.
- Internet routing: IP addresses share prefixes, and tries are used for longest prefix match routing.
- Memory vs speed tradeoff: Tries use more memory but offer O(k) search time, where k is the key length.
💾 Databases use trees for indexing (e.g., B-trees, B+ trees)
- Efficient range queries and lookups: Balanced trees ensure O(log n) insert/search/delete.
- Disk-friendly: B-trees minimize disk reads by keeping nodes wide and shallow.
- Used in practice: PostgreSQL, SQLite, and others use variants of B-trees for indexing.
🔐 Merkle trees
- Used in blockchains: Efficient verification of large data sets by checking only a small number of hashes.
- Tamper detection: Changing one leaf changes hashes all the way up—perfect for integrity checking.
- Applications: Bitcoin, Git, BitTorrent, and more rely on Merkle trees.
🌐 Spanning trees in networks
- Minimal spanning tree (MST): Ensures all nodes in a network are connected with minimal total edge weight.
- Used in routing: Algorithms like Kruskal’s or Prim’s help avoid loops in protocols like Ethernet (Spanning Tree Protocol).
🌳 Decision trees
- Machine learning: Trees split data based on feature thresholds to make predictions.
- Easy to interpret: Each path in the tree represents a rule for classification.
🔃 Sorting algorithms
- Binary heaps: Used in heap sort—trees where the parent is smaller/larger than children.
- BST-based sorts: In-order traversal of a Binary Search Tree gives sorted order.
- AVL/Red-Black Trees: Self-balancing trees used to maintain order during dynamic inserts/deletes.
🔍 Search algorithms
- Binary Search Trees (BSTs): Allow for fast search, insert, and delete in O(log n) time if balanced.
- Trie-based search: Efficient for prefix and word lookup.
- Tree traversal: DFS and BFS strategies apply directly—recursion meets queue/stack use in Rust.
Important Terms
- Root - the topmost node of the tree, only node without a parent
- Ancestor vs Descendant - If two nodes are connected, the node that is closer to the root is the ancestor of the other node, similarly the further node its descendant
- Parent vs Child - A nodes immediate descendant is its child, and a nodes immediate ancestor is its parent
- Leaf - a node with no child nodes
- Subtree - A subset of the tree, with a parent of the original tree becoming the root of the subtree
- Depth - the greatest number of descendants between the root and a leaf node
- Level - the number of edges between a node and the root. Root node has level 0
- Sibling - nodes that share the same parent
Why are binary trees useful?
- Simple to analyze
- Many algorithms boil down to a series of "True/False" decisions that map well to binary trees
- Ordering in particular fits well (either you are "<" or you aren't)
- Easy to use with recursive algorithms
What types of binary trees are there?
- Complete (every level except the last one are full)
- Perfect (all leaves are at the same level, all interior nodes have 2 children)
- Balanced (left and right subtrees differ by at most 1 level)
- Special
- Binary Heaps
- Binary Search Trees
Any other interesting trees?
- Prefix trees or tries
![[binary tree example]](modules/images/binary-tree-example.jpg)
Using Vectors to implement a Binary Tree
TreeNode struct and new() method
#[derive(Debug)]
struct TreeNode {
value: usize,
left: Option<usize>,
right: Option<usize>,
}
impl TreeNode {
// Constructor method
// This method creates a new TreeNode with the given value
// and initializes left and right child pointers to None
fn new(value: usize) -> Self {
TreeNode {
value,
left: None,
right: None,
}
}
}
BinaryTree struct and methods
#[derive(Debug)]
struct BinaryTree {
// A vector of TreeNode structs
// The index of the vector is the node index
nodes: Vec<TreeNode>,
root: Option<usize>,
}
impl BinaryTree {
// Constructor method
// This method creates a new BinaryTree with an empty vector of nodes
// and a root pointer set to None
fn new() -> Self {
BinaryTree { nodes: Vec::new(), root: None }
}
fn insert(&mut self, value: usize) {
let new_node_index = self.nodes.len();
self.nodes.push(TreeNode::new(value));
match self.root {
Some(root_index) => self.insert_at(root_index, new_node_index),
None => self.root = Some(new_node_index),
}
}
// Inserts a new node into a binary tree by updating the left or right child
// index of the current node, or if full, a left child node.
// * Start at the specified current node index:
// * if both children are empty, insert the left child
// * if left child is occupied, insert the right child
// * if both children are occupied, recursively attempt to insert the new
// node in the left subtree
fn insert_at(&mut self, current_index: usize, new_node_index: usize) {
let current_node = &mut self.nodes[current_index];
if current_node.left.is_none() {
current_node.left = Some(new_node_index);
} else if current_node.right.is_none() {
current_node.right = Some(new_node_index);
} else {
// Insert in left subtree for simplicity, could be more complex to keep balanced
let left = current_node.left.unwrap();
self.insert_at(left, new_node_index);
}
}
}
Remember that
leftandrightare indices, butvalueis the value we associated with the node.
- Predict the BinaryTree structure as we repeatedly insert.
let mut tree = BinaryTree::new();
tree.insert(1);
tree.insert(2);
tree.insert(3);
tree.insert(6);
tree.insert(7);
tree.insert(11);
tree.insert(23);
tree.insert(34);
println!("{:#?}", tree);
BinaryTree {
nodes: [
TreeNode {
value: 1,
left: Some(
1,
),
right: Some(
2,
),
},
TreeNode {
value: 2,
left: Some(
3,
),
right: Some(
4,
),
},
TreeNode {
value: 3,
left: None,
right: None,
},
TreeNode {
value: 6,
left: Some(
5,
),
right: Some(
6,
),
},
TreeNode {
value: 7,
left: None,
right: None,
},
TreeNode {
value: 11,
left: Some(
7,
),
right: None,
},
TreeNode {
value: 23,
left: None,
right: None,
},
TreeNode {
value: 34,
left: None,
right: None,
},
],
root: Some(
0,
),
}
Reminder: The numbers in the circles are the values, not the indices of the node.
![[binary tree]](modules/images/binary_tree.png)
This isn't super readable, is there a better way to output this tree?
Tree Traversal
There are several ways to traverse trees using algorithms we have seen before:
- Using BFS
- Level-order Traversal
- Using DFS
- Pre-order Traversal
- In-order Traversal
- Post Order Traversal
We are going to use level-order traversal to visit each level of the tree in order
Level-Order Traversal (BFS)
Just like before.
- Create an empty queue
- Add the root of tree to queue
- While the queue is not empty
- Remove node from queue and visit it
- Add the left child of node to the queue if it exists
- Add the right child of node to the queue if it exists
use std::collections::VecDeque;
fn level_order_traversal(tree: &BinaryTree) {
if let Some(root_index) = tree.root {
let mut queue = VecDeque::new();
queue.push_back(root_index);
while let Some(node_index) = queue.pop_front() {
let node = &tree.nodes[node_index];
println!("{}", node.value);
if let Some(left_index) = node.left {
queue.push_back(left_index);
}
if let Some(right_index) = node.right {
queue.push_back(right_index);
}
}
}
}
let mut tree2 = BinaryTree::new();
tree2.insert(1);
tree2.insert(2);
tree2.insert(3);
tree2.insert(6);
tree2.insert(7);
tree2.insert(11);
tree2.insert(23);
tree2.insert(34);
level_order_traversal(&tree2);
1
2
3
6
7
11
23
34
// Slightly more complex version that prints each level on a different line
use std::collections::VecDeque;
fn level_order_traversal2(tree: &BinaryTree) {
if let Some(root_index) = tree.root {
let mut queue = VecDeque::new();
queue.push_back(root_index);
while !queue.is_empty() {
let level_size = queue.len();
for _ in 0..level_size {
if let Some(node_index) = queue.pop_front() {
let node = &tree.nodes[node_index];
print!("{} ", node.value);
if let Some(left_index) = node.left {
queue.push_back(left_index);
}
if let Some(right_index) = node.right {
queue.push_back(right_index);
}
}
}
println!(); // New line after each level
}
}
}
let mut tree2 = BinaryTree::new();
tree2.insert(1);
tree2.insert(2);
tree2.insert(3);
tree2.insert(6);
tree2.insert(7);
tree2.insert(11);
tree2.insert(23);
tree2.insert(34);
level_order_traversal2(&tree2);
1
2 3
6 7
11 23
34
Depth Traversals
Pre-Order Traversal
Often used when making a copy of a tree, uses DFS
Algorithm:
- Visit the current node (e.g. print the current node value)
- Recursively traverse the current node's left subtree
- Recursively traverse the current node's right subtree
The pre-order traversal is a topologically sorted one, because a parent node is processed before any of its child nodes is done.
Reminder: The numbers in the circles are the values, not the indices of the node.
![[binary tree]](modules/images/binary_tree.png)
fn pre_order_traversal(tree: &BinaryTree, node_index: Option<usize>) {
if let Some(index) = node_index { // If the node index is not None
let node = &tree.nodes[index]; // Get the node at the index
println!("{}", node.value); // Visit (print) the current node value
pre_order_traversal(tree, node.left); // Traverse the left subtree
pre_order_traversal(tree, node.right); // Traverse the right subtree
}
}
pre_order_traversal(&tree2, tree2.root)
1
2
6
11
34
23
7
3
()
In-Order Traversal
In-Order traversal:
- Recursively traverse the current node's left subtree.
- Visit the current node (e.g. print the node's current value).
- Recursively traverse the current node's right subtree.
In a binary search tree ordered such that in each node the value is greater than all values in its left subtree and less than all values in its right subtree, in-order traversal retrieves the keys in ascending sorted order.
Reminder: The numbers in the circles are the values, not the indices of the node.
![[binary tree]](modules/images/binary_tree.png)
How do we update pre_order_traversal() to get in_order_traversal()?
fn in_order_traversal(tree: &BinaryTree, node_index: Option<usize>) {
if let Some(index) = node_index { // If the node index is not None
let node = &tree.nodes[index]; // Get the node at the index
in_order_traversal(tree, node.left); // Traverse the left subtree
println!("{}", node.value); // Visit (print) the current node value
in_order_traversal(tree, node.right); // Traverse the right subtree
}
}
in_order_traversal(&tree2, tree2.root)
34
11
6
23
2
7
1
3
()
Post-Order traversal
Good for deleting the tree or parts of it, must delete children before parents:
- Recursively traverse the current node's left subtree.
- Recursively traverse the current node's right subtree.
- Visit the current node.
Reminder: The numbers in the circles are the values, not the indices of the node.
![[binary tree]](modules/images/binary_tree.png)
How do we update in_order_traversal() to post_order_traversal()?
fn post_order_traversal(tree: &BinaryTree, node_index: Option<usize>) {
if let Some(index) = node_index { // If the node index is not None
let node = &tree.nodes[index]; // Get the node at the index
post_order_traversal(tree, node.left); // Traverse the left subtree
post_order_traversal(tree, node.right); // Traverse the right subtree
println!("{}", node.value); // Visit (print) the current node value
}
}
post_order_traversal(&tree2, tree2.root)
34
11
23
6
7
2
3
1
()
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Binary search trees
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
Understand binary search trees
-
Organize data into a binary tree
-
Similar to binary heaps where the parent was greater (or lesser) than either of its children
-
Binary Search Tree: the value of a node is greater than the values of all nodes in its left subtree and less than the value of all nodes in the right subtree.
-
Enables binary search for efficient lookup, addition and removal of items.
-
Each comparison skips half of the remaining tree.
-
Complexity for search, insert and delete is , assuming balanced trees.
![[sample tree]](modules/images/binary_search_tree.png)
- Invariant at each node:
- all left descendants parent
- parent all right descendants
![[sample tree]](modules/images/relationship.png)
- Compared to binary heaps:
- different ordering of elements
Basic operations: find a key
How can we do this?
- Descend recursively from the root until found or stuck:
- If current node key is , return.
- If value at the current node, go left
- If value at the current node, go right
- If finished searching, return not found
Basic operations: insert a key
How can we do this?
- Keep descending from the root until you leave the tree
- If value at the current node, go left
- If value at the current node, go right
- Create a new node containing there
Basic operations: delete a node
How can we do this?
This can be more complicated because we might have to find a replacement.
Case 1 -- Leaf Node
If node is a leaf node, just remove and return.
Case 2 -- One Child
If node has only one child, remove and move the child up.
Example: Remove 4.
7
/ \
4 11
\
6
Remove 4 and move 6 up.
7
/ \
6 11
Case 3 -- Else
Otherwise, find the left-most descendant of the right subtree and move up.
This is the inorder successor.
Example? Remove 4.
7
/ \
4 11
/ \
2 6
/ \ / \
1 3 5 8
In this case it is 5, so replace 4 with 5.
7
/ \
5 11
/ \
2 6
/ \ \
1 3 8
Cost of these operations?
Bad news: the depth can be made proportional to , the number of nodes. How?
Good news: smart ways to make the depth
Balanced binary search trees
There are smart ways to rebalance the tree!
- Depth:
Binary search trees -- Implementation
- Applications (range searching)
- Rust:
BTreeMapandBTreeSet - Tries (Prefix Trees)
-
Let's slightly revise our
TreeNodeandBinaryTreestructs and methods. -
The main difference is the
insert_at()function.
#[derive(Debug)]
struct TreeNode {
value: usize,
left: Option<usize>,
right: Option<usize>,
}
impl TreeNode {
fn new(value: usize) -> Self {
TreeNode {
value,
left: None,
right: None,
}
}
}
#[derive(Debug)]
struct BinaryTree {
nodes: Vec<TreeNode>,
root: Option<usize>,
}
impl BinaryTree {
fn new() -> Self {
BinaryTree { nodes: Vec::new(), root: None }
}
fn insert(&mut self, value: usize) {
let new_node_index = self.nodes.len();
self.nodes.push(TreeNode::new(value));
match self.root {
Some(root_index) => self.insert_at(root_index, new_node_index, value),
None => self.root = Some(new_node_index),
}
}
fn insert_at(&mut self, current_index: usize, new_node_index: usize, value:usize) {
let current_node = &mut self.nodes[current_index];
if current_node.value < value {
if current_node.right.is_none() {
current_node.right = Some(new_node_index);
} else {
let right = current_node.right.unwrap();
self.insert_at(right, new_node_index, value);
}
} else {
if current_node.left.is_none() {
current_node.left = Some(new_node_index);
} else {
let left = current_node.left.unwrap();
self.insert_at(left, new_node_index, value);
}
}
}
}
- What happens if we insert the following values?
let mut tree = BinaryTree::new();
tree.insert(1);
tree.insert(2);
tree.insert(3);
tree.insert(6);
tree.insert(7);
tree.insert(11);
tree.insert(23);
tree.insert(34);
println!("{:#?}", tree);
BinaryTree {
nodes: [
TreeNode {
value: 1,
left: None,
right: Some(
1,
),
},
TreeNode {
value: 2,
left: None,
right: Some(
2,
),
},
TreeNode {
value: 3,
left: None,
right: Some(
3,
),
},
TreeNode {
value: 6,
left: None,
right: Some(
4,
),
},
TreeNode {
value: 7,
left: None,
right: Some(
5,
),
},
TreeNode {
value: 11,
left: None,
right: Some(
6,
),
},
TreeNode {
value: 23,
left: None,
right: Some(
7,
),
},
TreeNode {
value: 34,
left: None,
right: None,
},
],
root: Some(
0,
),
}
1
\
2
\
3
\
6
\
7
\
11
\
23
\
34
Unbalanced binary search trees can be inefficient!
This is a degenerate tree -- basically a linked list.
Balanced binary search trees
There are smart ways to rebalance the tree!
-
Depth:
-
Usually additional information has to be kept at each node
-
Many popular, efficient examples:
- Red–black trees
- AVL trees
- BTrees (Used in Rust)
- ...
Fundamentally they all support rebalancing operations using some form of tree rotation.
We'll look at some simple approaches.
Basic operations: rebalance a tree
How can we do this?
-
Quite a bit more complicated
-
One basic idea. Find the branch that has gotten too long
- Swap the parent with the child that is at the top of the branch by making the child the parent and the parent the child
- If you picked a left child take the right subtree and make it a left child of the old parent
- if you picked a right child take left subtree and make it a right child of the old parent
Example
Let's go back to our degenerate tree. It's just one long branch.
1
\
2
\
3
\
6
\
7
\
11
\
23
\
34
Step 1: Rotate around 1-2-3.
2
/ \
1 3
\
6
\
7
\
11
\
23
\
34
Step 2: Rotate around 3-6-7.
2
/ \
1 6
/ \
3 7
\
11
\
23
\
34
Step 3: Rotate around 7-11-23.
2
/ \
1 6
/ \
3 11
/ \
7 23
\
34
A simple way to rebalance a binary tree
- First do an in-order traversal to get the nodes in sorted order
- Then use the middle of the sorted vector to be the root of the tree and recursively build the rest
impl BinaryTree {
fn in_order_traversal(&self, node_index: Option<usize>)->Vec<usize> {
let mut u: Vec<usize> = vec![];
if let Some(index) = node_index {
let node = &self.nodes[index];
u = self.in_order_traversal(node.left);
let mut v: Vec<usize> = vec![node.value];
let mut w: Vec<usize> = self.in_order_traversal(node.right);
u.append(&mut v);
u.append(&mut w);
}
return u;
}
}
let mut z = tree.in_order_traversal(tree.root);
z.sort();
println!("{:?}", z);
[1, 2, 3, 6, 7, 11, 23, 34]
impl BinaryTree {
// This function recursively builds a perfectly balanced BST by:
// 1. Finding the middle element of a sorted array to use as the root
// 2. Recursively building the left and right subtrees using the elements
// before and after the middle element, respectively.
fn balance_bst(&mut self, v: &[usize], start:usize, end:usize) -> Option<usize> {
if start >= end {
return None;
}
let mid = (start+end) / 2;
let node_index = self.nodes.len();
self.insert(v[mid]);
self.nodes[node_index].left = self.balance_bst(v, start, mid);
self.nodes[node_index].right = self.balance_bst(v, mid+1, end);
Some(node_index)
}
}
let mut bbtree = BinaryTree::new();
bbtree.balance_bst(&z, 0, z.len());
println!("{:#?}", bbtree);
println!("{:?}", level_order_traversal2(&bbtree));
BinaryTree {
nodes: [
TreeNode {
value: 7,
left: Some(
1,
),
right: Some(
5,
),
},
TreeNode {
value: 3,
left: Some(
2,
),
right: Some(
4,
),
},
TreeNode {
value: 2,
left: Some(
3,
),
right: None,
},
TreeNode {
value: 1,
left: None,
right: None,
},
TreeNode {
value: 6,
left: None,
right: None,
},
TreeNode {
value: 23,
left: Some(
6,
),
right: Some(
7,
),
},
TreeNode {
value: 11,
left: None,
right: None,
},
TreeNode {
value: 34,
left: None,
right: None,
},
],
root: Some(
0,
),
}
7
3 23
2 6 11 34
1
()
Produces the result:
7
/ \
3 23
/ \ / \
2 6 11 34
/
1
Why use binary search trees?
- Hash maps and hash sets give us time operations?
Reason 1:
- Good worst case behavior: no need for a good hash function
Reason 2:
- Can answer efficiently questions such as:
- What is the smallest/greatest element?
- What is the smallest element greater than ?
- List all elements between and
Example: find the smallest element greater than
Question: How can you list all elements in order in time?
Answer: recursively starting from the root
- visit left subtree
- output current node
- visit right subtree
Outputting smallest element greater than :
- Like above, ignoring whole subtrees smaller than
- Will get the first element greater than in time
For balanced trees: listing first greater elements takes time
-Trees
Are there binary search trees in Rust's standard library?
-
Not exactly
-
Binary Search Trees are computationally very efficent for search/insert/delete ().
-
In practive, very inefficient on modern computer architectures.
- Every insert triggers a heap allocation
- Every single comparison is a cache-miss.
Enter -trees:
-
B-trees are balanced search trees where each node contains between B and 2B keys, with one more subtree than keys.
-
All leaf nodes are at the same depth, ensuring consistent O(log n) performance for search, insert, and delete operations.
-
B-trees are widely used in database systems for indexing and efficient range queries.
-
They're implemented in Rust's standard library as
BTreeMapandBTreeSetfor in-memory operations. -
The structure is optimized for both disk and memory operations, with nodes sized appropriately for the storage medium.

By CyHawk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=11701365
What does the B stand for?
Invented by Bayer and McCreight at Boeing. Suggested explanations have been Boeing, balanced, broad, bushy, and Bayer. McCreight has said that "the more you think about what the B in B-trees means, the better you understand B-trees.
BTreeSet and BTreeMap
std::collections::BTreeSet
std::collections::BTreeMap
Sets and maps, respectively
// let's create a set
use std::collections::BTreeSet;
let mut set: BTreeSet<i32> = BTreeSet::new();
set.insert(11);
set.insert(7);
set.insert(5);
set.insert(23);
set.insert(25);
// listing a range
set.range(7..25).for_each(|x| println!("{}", x));
7
11
23
// listing a range: left and right bounds and
// whether they are included or not
use std::ops::Bound::{Included,Excluded};
set.range((Excluded(5),Included(11))).for_each(|x| println!("{}", x));
7
11
// Iterating through the items is the in-order traversal that will give you sorted output
for i in &set {
println!("{}", *i);
}
5
7
11
23
25
()
// let's make a map now
use std::collections::BTreeMap;
// We can rely on type inference to avoid having to fully write out the types
let mut map = BTreeMap::new();
map.insert("DS310", "Data Mechanics");
map.insert("DS210", "Programming for Data Science");
map.insert("DS120", "Foundations of Data Science I");
map.insert("DS121", "Foundations of Data Science II");
map.insert("DS122", "Foundations of Data Science III");
// Try to find a course
if !map.contains_key("DS111") {
println!("Course not found");
}
Course not found
()
for (course, name) in &map {
println!("{course}: \"{name}\"");
}
DS120: "Foundations of Data Science I"
DS121: "Foundations of Data Science II"
DS122: "Foundations of Data Science III"
DS210: "Programming for Data Science"
DS310: "Data Mechanics"
()
Note that the keys are sorted.
// listing a range
map.range("DS000".."DS199").for_each(|(x,y)| println!("{}: \"{}\"", x, y));
DS120: "Foundations of Data Science I"
DS121: "Foundations of Data Science II"
DS122: "Foundations of Data Science III"
BTreeMap vs HashMap
-
Use HashMap when:
- You need O(1) average-case lookup time for specific keys
- You don't need to maintain any particular order of elements
- You're doing mostly individual key lookups rather than range queries
- Your keys implement
Hash,Eq, andPartialEqtraits
-
Use BTreeMap when:
- You need to efficiently list all values in a specific range
- You need ordered iteration over keys/values
- You need to find the smallest/greatest element or elements between two values
- You need consistent O(log n) performance for all operations
- Your keys implement
Ordtrait
-
Key Differences:
- HashMap provides O(1) average-case lookup but can have O(n) worst-case
- BTreeMap provides guaranteed O(log n) performance for all operations
- BTreeMap maintains elements in sorted order
- HashMap is generally faster for individual lookups when you don't need ordering
-
Practical Examples:
- Use HashMap for: counting word frequencies, caching, quick lookups
- Use BTreeMap for: maintaining ordered data, range queries, finding nearest values
-
Memory Considerations:
- HashMap may use more memory due to its underlying array structure which needs resizing (doubling and copyng) when full
- BTreeMap's memory usage is more predictable and grows linearly with the number of elements -- adds new nodes as needed.
Prefix Tree (Trie)
Can be pronounced /ˈtraɪ/ (rhymes with tide) or /ˈtriː/ (tree).
A very efficient data structure for dictionary search, word suggestions, error corrections etc.
A trie for keys "A", "to", "tea", "ted", "ten", "i", "in", and "inn". Each complete English word has an arbitrary integer value associated with it. Wikipedia
Available in Rust as an external create https://docs.rs/trie-rs/latest/trie_rs/
:dep trie-rs="0.1.1"
fn testme() {
use std::str;
use trie_rs::TrieBuilder;
let mut builder = TrieBuilder::<u8>::new();
builder.push("to");
builder.push("tea");
builder.push("ted");
builder.push("ten");
builder.push("teapot");
builder.push("in");
builder.push("inn");
let trie = builder.build();
println!("Find suffixes of \"te\"");
let results_in_u8s: Vec<Vec<u8>> = trie.predictive_search("te");
let results_in_str: Vec<&str> = results_in_u8s
.iter()
.map(|u8s| str::from_utf8(u8s).unwrap())
.collect();
println!("{:?}", results_in_str);
}
testme();
Find suffixes of "te"
["tea", "teapot", "ted", "ten"]
To Insert a Word
-
Start at the Root
- Begin at the root node of the trie
- The root node represents an empty string
-
Process Each Character
- For each character in the word you want to insert:
- Check if the current node has a child node for that character
- If yes: Move to that child node
- If no: Create a new node for that character and make it a child of the current node
- For each character in the word you want to insert:
-
Mark the End
- After processing all characters, mark the final node as an end-of-word node
- This indicates that a complete word ends at this node
Let me illustrate with an example. Suppose we want to insert the word "tea" into an empty trie:
Step 1: Start at root
(root)
Step 2: Insert 't'
(root)
|
t
Step 3: Insert 'e'
(root)
|
t
|
e
Step 4: Insert 'a'
(root)
|
t
|
e
|
a*
Step 5: Mark 'a' as end-of-word (shown with *)
If we then insert "ted", the trie would look like:
(root)
|
t
|
e
/ \
a* d*
The asterisk (*) marks nodes where words end. This structure allows us to:
- Share common prefixes between words
- Efficiently search for words
- Find all words with a given prefix
- Check if a word exists in the trie
Most likely your spellchecker is based on a trie
In this case, we will compare possible close matches and then sort by frequency of occurence in some corpus and present top 3-5.
If your word is not in the trie do the following:
- Step 1: Find the largest prefix that is present and find the trie words with that prefix
- Step 2: Delete the first letter from your word and redo Step 1
- Step 3: Insert a letter (for all letters) to the beginning of the word and redo Step 1
- Step 4: Replace the beginning letter with a different one (for all letters) and redo Step 1
- Step 5: Transpose the first two letters and redo Step 1
- Step 6: Collect all words from Steps 1-5 sort by frequency of occurrence and present top 3-5 to user
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Algorithm Design
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
Big picture
Review a few approaches to algorithm design:
- Greedy approach
- Divide and conquer
Others:
- Dynamic Programming
- Branch and Bound
- Backtracking
You'll likely see these in DS320 -- Algorithms for Data Science
Why do we care about algorithm design?
- Many problems share similar structure
- Having an algorithmic approach for a certain style of problem makes things a lot easier!
- Different approaches have tradeoffs depending on what you want to prioritize
Algorithms to Live By

From book page.
A fascinating exploration of how computer algorithms can be applied to our everyday lives, helping to solve common decision-making problems and illuminate the workings of the human mind.
All our lives are constrained by limited space and time, limits that give rise to a particular set of problems. What should we do, or leave undone, in a day or a lifetime? How much messiness should we accept? What balance of new activities and familiar favorites is the most fulfilling? These may seem like uniquely human quandaries, but they are not: computers, too, face the same constraints, so computer scientists have been grappling with their version of such problems for decades. And the solutions they’ve found have much to teach us.
In a dazzlingly interdisciplinary work, acclaimed author Brian Christian and cognitive scientist Tom Griffiths show how the simple, precise algorithms used by computers can also untangle very human questions. They explain how to have better hunches and when to leave things to chance, how to deal with overwhelming choices and how best to connect with others. From finding a spouse to finding a parking spot, from organizing one’s inbox to understanding the workings of human memory, Algorithms to Live By transforms the wisdom of computer science into strategies for human living.
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Greedy algorithms
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
Greedy algorithms
- Make locally best (or any) decision towards solving a problem
Warm Up: Coin Change Problem
You are a cashier and you need to give US $0.43 back to your customer.
Problem: We want to find the smallest number of coins that sum up to a given value.
Assumption: We're not limited by number of coins in any denomination.
Input: Set of coin denominations, Target value
Output: Minimal set of coins adding up to value
What would a greedy approach look like here?
Idea: Pick the largest denomination for the remaining value and repeat until done.
Let's try it out.
fn coin_change(denominations: &[usize], value: usize) {
// Arguments:
// denominations: list of coin denominations sorted in decreasing value
// value: target value we are trying to match
// count notes using Greedy approach
let mut coin_counter = vec![0; denominations.len()];
let mut remainder = value;
for i in 0..denominations.len() {
// will at least one of the current denomination work?
if remainder >= denominations[i] {
// check how many of denomination i we can use.
coin_counter[i] = remainder / denominations[i];
remainder = remainder % denominations[i];
}
}
// Print notes
println!("Currency Count ->");
for i in 0..denominations.len() {
if coin_counter[i] != 0 {
println!("{} : {}", denominations[i], coin_counter[i]);
}
}
}
let denoms = [25,10,5,1]; // US coin denominations in decreasing order
let val = 41;
coin_change(&denoms, val);
Currency Count ->
25 : 1
10 : 1
5 : 1
1 : 1
// lets try a different set of denominations
let denoms = [25,15,1];
let val = 30;
coin_change(&denoms, val);
Currency Count ->
25 : 1
1 : 5
Warning: The greedy approach is only optimal for certain sets of denominations! These are known as canonical coin systems.
Canonical Coin System:
For the greedy algorithm to work correctly and always give the minimum number of coins, the coin denominations must have the following property:
- The denominations must be in a "canonical" system, meaning that each coin value is at least twice the value of the next smaller denomination.
This fails because 25 is not at least twice the value of 15.
When this property doesn't hold (like in our example with
[25, 15, 1]), we need to use a more sophisticated algorithm like dynamic programming to find the optimal solution.
Is there a country with an non-canonical coin system?
// United Kingdom before decimalization in 1971
let denoms = [30,24,12,6,3,1];
let val = 48;
coin_change(&denoms, val);
Currency Count ->
30 : 1
12 : 1
6 : 1
We could have done better with 2x 24p.
Data science connection in a future lecture
- Heuristics for creating decision trees
- select "best" single split and recurse
Example we have seen
- Shortest paths (Dijkstra's algorithm)
- select the vertex known to be closest
- try routing paths through it
- Gives globally optimal solution!!!
Another Example: Minimum spanning tree
Find cheapest overall subset of edges so that the graph is connected
-
Kruskal's algorithm: keep adding the cheapest edge that connects disconnected groups vertices
-
Complexity
Why is MST useful?
-
Connecting N locations with fiber using the least amount of fiber
-
Traveling salesman approximate solution
Algorithm Outline
Start with a graph with weighted edges.
Disconnect all edges...
- Find the cheapest edge remaining
- Look at the 2 nodes it connects and find the root of the tree they belong to
- If they belong to the same tree go back to step 1
- Else join the two trees into a single tree
Define Graph Structure
We'll define a modified graph structure that simultaneously represents a weighted undirected graph and a tree.
type Vertex = usize;
type Distance = usize;
type Edge = (Vertex, Vertex, Distance);
#[derive(Debug,Copy,Clone)]
struct Outedge {
vertex: Vertex,
length: Distance,
}
type AdjacencyList = Vec<Outedge>;
// We're updating this struct to include parent and rank
#[derive(Debug)]
struct Graph {
n: usize,
outedges: Vec<Edge>, // list of edges
parent: Vec<Vertex>, // parent[i] is the parent ID of node i
rank: Vec<usize>, // how deep is the tree rooted at this node?
}
impl Graph {
fn create_undirected(n:usize, outedges:Vec<Edge>) -> Graph {
// Create a graph from a list of edges
//
// This function creates a graph from a list of edges and initializes
// the parent and rank vectors. It also sorts the edges by distance.
// Internally, the graph is represented as a list of edges, a parent
// vector, and a rank vector, with parents and ranks indexed in the
// same order as the outedges vector.
//
// Arguments:
// n: number of nodes
// outedges: list of edges
// Returns:
// Graph: a graph with the given number of nodes and edges
// Initialize parent and rank vectors
let parent: Vec<Vertex> = vec![];
let rank: Vec<usize> = vec![];
// Create the graph
let mut g = Graph{n,outedges,parent,rank};
// Sort the edges by distance O(n log n)
g.outedges.sort_by(|a, b| a.2.cmp(&b.2));
// Initialize parent and rank vectors
// From a tree perspective, it's just a forest of single node "trees"
for node in 0..g.n {
// The parent and rank vectors are indexed in the same order
// as the outedges vector
g.parent.push(node); // set each node to be its own parent
g.rank.push(0); // set the rank of each node to 0
}
g
}
fn find(&mut self, i:Vertex) -> Vertex {
// Recursively find the root of the tree rooted at i.
// O(log n) -- logarithmic time
//
// Arguments:
// i: node to find the root of
// Returns:
// Vertex: the root of the tree rooted at i
if self.parent[i] != i {
self.parent[i] = self.find(self.parent[i]);
}
return self.parent[i];
}
fn union(&mut self, i:Vertex, j:Vertex) {
// Union the trees rooted at i and j by making the root of the
// smaller ranked tree a child of the root of the larger tree.
// O(1) -- constant time
//
// Arguments:
// i: node to union with
// j: node to union with
if self.rank[i] < self.rank[j] {
self.parent[i] = j;
} else if self.rank[i] > self.rank[j] {
self.parent[j] = i;
} else {
self.parent[j] = i;
self.rank[i] += 1;
}
}
}
Let's consider the following graph.
// Let's create the graph
let n = 9;
let edges: Vec<Edge> = vec![(7,6,1),(8,2,2),(6,5,2),(0,1,4),(2,5,4),(8,6,6),(2,3,7),(7,8,7),(0,7,8),(1,2,8),(3,4,9),(5,4,10),(1,7,11),(3,5,14)];
let mut g = Graph::create_undirected(n, edges);
g
Graph { n: 9, outedges: [(7, 6, 1), (8, 2, 2), (6, 5, 2), (0, 1, 4), (2, 5, 4), (8, 6, 6), (2, 3, 7), (7, 8, 7), (0, 7, 8), (1, 2, 8), (3, 4, 9), (5, 4, 10), (1, 7, 11), (3, 5, 14)], parent: [0, 1, 2, 3, 4, 5, 6, 7, 8], rank: [0, 0, 0, 0, 0, 0, 0, 0, 0] }
Kruskal's MST
impl Graph {
fn KruskalMST(&mut self) -> Vec<Edge> {
// Arguments:
// self: a mutable reference to the graph
// Returns:
// Vec<Edge>: a vector of edges that form the minimum spanning tree
// Initialize the result vector and counters
let mut result: Vec<Edge> = vec![];
let mut num_mst_e = 0;
let mut next_edge = 0; // start with the smallest weighted edge
// Loop until we built a tree that has n-1 edges
// A tree with n nodes has n-1 edges
while num_mst_e < self.n - 1 { // O(n)
let (u,v,w) = self.outedges[next_edge];
next_edge = next_edge + 1;
let x = self.find(u); // find the root of u
let y = self.find(v); // find the root of v
// If u and v are in different trees, add the edge to the MST
if x != y {
num_mst_e += 1;
result.push((u,v,w));
self.union(x,y); // join the two trees at their roots
}
}
result
}
}
Complexity Analysis
whileloop -- times- Insde the loop
- for each of 2
.find() - Constant time for the
.union()
- for each of 2
Which, in order notation would be:
let result = g.KruskalMST();
let mut min_cost = 0;
for (u,v,w) in result {
min_cost += w;
println!("{} -- {} == {}", u, v, w)
}
println!("Spanning Tree Cost {}", min_cost);
7 -- 6 == 1
8 -- 2 == 2
6 -- 5 == 2
0 -- 1 == 4
2 -- 5 == 4
2 -- 3 == 7
0 -- 7 == 8
3 -- 4 == 9
Spanning Tree Cost 37
Other interesting graph problems (independent reading if you are interested)
- Matching: matching conference attendees to available desserts they like
- Another formulation: maximum size set of independent edges in graph
- Keep adding edges as long as you can
- This will give factor 2 approximation
Traveling Salesman Approximation using MST
- Make a MST
- Pick an arbitrary vertex to be the root of the tree
- Run DFS from the root
- Shortcut where you can to shorten the tour.
For example a DFS of the above tree might yield:
0 - 1 - 0 - 7 - 6 - 5 - 2 - 8 - 2 - 3 - 4 - 3 - 2 - 5 - 6 - 7 - 0
Whenever you go to a new node through an already visited node, check to see if you can get there directly with less cost:
0 - 1 - (0) - 7 - 6 - 5 - 2 - 8 - 2 - 3 - 4 - (3 - 2) - 5 - 6 - 7 - 0
This is still not optimal but guaranteed to be within 2x of optimal (proof beyond our scope)
Greedy Algorithms Recap
- They often work well in practice
- They are polynomial on the size of their input (e.g. or better)
- They don't always find the best solutions (recall the coin problem with non-canonical denominations)
- They definitely don't prove that P != NP :-)
P vs NP
-
P represents the class of problems that can be solved in polynomial time.
-
NP represents the class of problems where solutions are unknown, but solutions can be verified in polynomial time
-
If a problem is NP, is it also P?
-
Answer this and get $1M
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Divide and conquer
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
Applies to a class of problem where it might be difficult to solve directly, but the problem can be easily subdivided.
If your problem is too difficult:
- partition it into subproblems
- solve the subproblems
- combine their solutions into a solution to the entire problem
We'll look at 3 algorithms
- Simple averaging
- Merge Sort
- Quick Sort
Warm Up: Taking the average of an array
How can we use a divide and conquer approach to taking the average of an array?
How would you do this?
fn divide_and_conquer_average(arr: &[f64]) -> (f64, usize) {
// A divide and conquer approach to finding the average of an array using
// recursion.
//
// This function takes a slice of floating point numbers and returns a tuple
// containing the average and the number of elements in the array.
//
// Arguments:
// arr: A slice of floating point numbers
//
// Returns:
// A tuple containing the average and the number of elements in the array
if arr.len() == 1 {
return (arr[0], 1);
} else {
let mid = arr.len() / 2;
let (left_sum, left_count) = divide_and_conquer_average(&arr[..mid]);
let (right_sum, right_count) = divide_and_conquer_average(&arr[mid..]);
return (left_sum + right_sum, left_count + right_count)
}
}
let arr = [1.0, 28.0, 32.0, 41.0, 25.0];
let (total, num) = divide_and_conquer_average(&arr);
println!("The average is {}", total/num as f64);
let straightforward_avg = arr.iter().sum::<f64>() / arr.len() as f64;
println!("The straightforward average is {}", straightforward_avg);
The average is 25.4
The straightforward average is 25.4
Is this actually more efficient than the straightforward approach?
No! Why?
Answer:
We are subdividing to levels and at level we are doing additions, so total
The sum of the first terms of a geometric series is:
Plug in and and simplify.
Using properties of logarithms:
Final Answer:
This holds for N a power of 2.
It is still a useful toy example though
Our plan: see two classic divide and conquer sorting algorithms
Merge Sort
Recursively:
- sort the first half
- sort the second half
- merge the results
- Merging two lists of and elements takes time, or
- levels of recursion: work on each level
- time overall
BUT
- Difficult to do in-place (requires extra memory allocations for intermediate results)
Implementing merging
fn merge(v1:Vec<i32>, v2:Vec<i32>) -> Vec<i32> {
// Take two sorted vectors and merge them into a single sorted vector
//
// This function takes two vectors of integers and returns a new vector
// containing all the elements from both vectors in sorted order.
//
// Arguments:
// v1: A sorted vector of integers
// v2: A sorted vector of integers
//
// Returns:
// A new vector containing all the elements from both vectors in sorted order
let (l1,l2) = (v1.len(), v2.len());
let mut merged = Vec::with_capacity(l1+l2); // preallocate memory
let (mut i1, mut i2) = (0,0);
while i1 < l1 {
if (i2 == l2) || (v1[i1] <= v2[i2]) {
merged.push(v1[i1]);
i1 += 1;
} else {
merged.push(v2[i2]);
i2 += 1;
}
}
while i2 < l2 {
merged.push(v2[i2]);
i2 += 1;
}
merged
}
let v1 = vec![3,4,8,11,12];
let v2 = vec![1,2,3,9,22];
merge(v1,v2)
[1, 2, 3, 3, 4, 8, 9, 11, 12, 22]
Implementing Merge Sort
Now implement divide and conquer via recursion.
fn merge_sort(input:&[i32]) -> Vec<i32> {
// Implement merge sort using divide and conquer
//
// This function takes a slice of integers and returns a new vector
// containing all the elements from the input slice in sorted order.
//
// Arguments:
// input: A slice of integers
//
// Returns:
// A new vector containing all the elements from the input slice in sorted order
if input.len() <= 1 {
input.to_vec()
} else {
let split = input.len() / 2;
let v1 = merge_sort(&input[..split]);
let v2 = merge_sort(&input[split..]);
merge(v1,v2)
}
}
let v = vec![2,4,21,6,2,32,62,0,-2,8];
merge_sort(&v)
[-2, 0, 2, 2, 4, 6, 8, 21, 32, 62]
See merge_sort Cargo project if you want to debug.
Quick Sort
- Select an arbitrary (random?) element from the array
- Partition your vector:
- Move elements lower than to the left
- Move elements greater than to the right
- which will result in 3 partitions:
- the left partition
- the middle partition (in the correct location(s))
- the right partition
- Repeat again for the left and right partitions
- Partitioning elements takes time
- Intuition: The size of the problem usually decreases by constant factor in a recursive call
- Expected time: time overall (probabilistic algo analysis)
- but worst case when the array is already sorted and pivot is always first or last element.
- recursive calls and each level does about comparisons.
Implementing partitioning
fn partition(input:&mut [i32], pivot: i32) -> (usize,usize) {
// move numbers lower than pivot to the left
let mut left = 0;
for i in 0..input.len() {
if input[i] < pivot {
input.swap(i,left);
left += 1;
}
}
// now input[..left] are all numbers lower than pivot
// move numbers greater than pivot to the right
let mut right = input.len();
for i in (left..input.len()).rev() {
if input[i] > pivot {
right -= 1;
input.swap(i,right);
}
}
// input[right..]: numbers greater than pivot
// left is the index of the pivot and
// right is the index of the first number greater than pivot
(left,right)
}
Implementing QuickSort
:dep rand
use rand::Rng;
fn quicksort(input:&mut [i32]) {
if input.len() >= 2 {
// pivot = random element from the input
let pivot = input[rand::rng().random_range(0..input.len())];
// partition the input array around the pivot
let (left,right) = partition(input, pivot);
println!("\nL {} R {} P {} P {}", left, right, pivot, input[left]);
println!("Left side {:?}", &input[..left]);
println!("Right side {:?}", &input[right..]);
quicksort(&mut input[..left]);
quicksort(&mut input[right..]);
}
}
let mut q = vec![145,12,3,7,83,12,8,64];
quicksort(&mut q);
println!("{:?}", q);
L 7 R 8 P 145 P 145
Left side [12, 3, 7, 83, 12, 8, 64]
Right side []
L 6 R 7 P 83 P 83
Left side [12, 3, 7, 12, 8, 64]
Right side []
L 5 R 6 P 64 P 64
Left side [12, 3, 7, 12, 8]
Right side []
L 1 R 2 P 7 P 7
Left side [3]
Right side [12, 12, 8]
L 1 R 3 P 12 P 12
Left side [8]
Right side []
[3, 7, 8, 12, 12, 64, 83, 145]
See quicksort Cargo project to single step debug.
Recap of Divide and Conquer algorithms
- They divide the problems into smaller subproblems
- They are always polynomial in execution time
- They tell us nothing about P and NP
Note on Recursion in Rust
Recursion with mutable references can be quite hard in Rust due to the borrow checker
A relatively simple example of the problem.
We want to make another mutable reference to the first element and pass the rest of the slice to the recursive call.
fn process_slice(slice: &mut [i32]) {
if !slice.is_empty() {
let first = &mut slice[0]; // Mutable borrow of the first element
process_slice(&mut slice[1..]); // Recursive call borrows the rest of the slice mutably
*first *= 2; // Attempt to modify the first element after recursive call
}
}
fn testme() {
let mut numbers = [1, 2, 3, 4];
process_slice(&mut numbers);
println!("{:?}", numbers);
}
testme();
[E0499] Error: cannot borrow `*slice` as mutable more than once at a time
╭─[command_2:1:1]
│
3 │ let first = &mut slice[0]; // Mutable borrow of the first element
│ ──────┬──────
│ ╰──────── first mutable borrow occurs here
4 │ process_slice(&mut slice[1..]); // Recursive call borrows the rest of the slice mutably
│ ──┬──
│ ╰──── second mutable borrow occurs here
5 │ *first *= 2; // Attempt to modify the first element after recursive call
│ ─────┬─────
│ ╰─────── first borrow later used here
───╯
The unsafe language feature allows you to bypass the borrow checker but it is not recommended and not covered in this class. A very small example below
fn process_slice(slice: *mut i32, len: usize) {
if len == 0 {
return;
}
unsafe {
// Access and modify the first element
let first = &mut *slice;
// Recursive call with the rest of the slice
let rest = slice.add(1); // Advance the pointer to the next element
process_slice(rest, len - 1);
*first *= 2;
}
}
fn testme() {
let mut numbers = [1, 2, 3, 4];
let len = numbers.len();
unsafe {
process_slice(numbers.as_mut_ptr(), len);
}
println!("{:?}", numbers); // Output: [2, 4, 6, 8]
}
testme();
[2, 4, 6, 8]
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
NDArray
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
-
An -dimensional (e.g. 1-D, 2-D, 3-D, ...) container for general elements and numerics.
-
Similar to Python's Numpy but with important differences.
-
Rich set of methods for creating views and slices into the array
-
Provides a rich set of methods and mathematical operations
Key similarities with Python Numpy (from link)
- Arrays have single element types
- Arrays can have arbitrary dimensions
- Arrays can have arbitrary strides
- Indexing starts at 0
- Default ordering is row-major (more on that below)
- Arithmetic operators (+, -, *, /) perform element-wise operations
- Arrays that are not views are contiguous in memory
- Many cheap operations that return views into the array instead of copying data
Some important differences from Numpy
- Numpy arrays and views are all mutable and can all change the contents of an array.
- NDarrays have:
- flavors that can change contents,
- flavors that cannot, and
- flavors that make copies when things change.
- Numpy arrays are always dynamic in their number of dimensions. NDarrays can be static or dynamic.
- Slices with negative steps behave differently (more on that later)
To use it
To add latest ndarray crate.
% cargo add ndarray
or manually add
[dependencies]
ndarray="0.15.6"
or later in your Cargo.toml file
Why use NDarray over Vec or array?
It is easier to do a bunch of things like:
- Data Cleaning and Preprocessing offering functions like slicing and fill
- Statistics built in (lots of math functions come with it)
- Machine learning: Used in many of the ML libraries written in Rust
- Linear Algebra: Built in methods like matrix inversion, multiplication and decomposition.
Let's look at some example usage.
// This is required in a Jupyter notebook. // For a cargo project, you would add it to your Cargo.toml file. :dep ndarray = { version = "^0.15.6" } use ndarray::prelude::*; fn main() { let a = array![ // handy macro for creating arrays [1.,2.,3.], [4.,5.,6.], ]; assert_eq!(a.ndim(), 2); // get the number of dimensions of array a assert_eq!(a.len(), 6); // get the number of elements in array a assert_eq!(a.shape(), [2, 3]); // get the shape of array a assert_eq!(a.is_empty(), false); // check if the array has zero elements println!("Print the array with debug formatting:"); println!("{:?}", a); println!("\nPrint the array with display formatting:"); println!("{}", a); } main();
Print the array with debug formatting:
[[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0]], shape=[2, 3], strides=[3, 1], layout=Cc (0x5), const ndim=2
Print the array with display formatting:
[[1, 2, 3],
For a side by side comparison NumPy, see https://docs.rs/ndarray/latest/ndarray/doc/ndarray_for_numpy_users/index.html
Array Creation
| NumPy | ndarray | Notes |
|---|---|---|
| np.array([[1.,2.,3.], [4.,5.,6.]]) | array![[1.,2.,3.], [4.,5.,6.]] or arr2(&[[1.,2.,3.], [4.,5.,6.]]) | 2×3 floating-point array literal |
| np.arange(0., 10., 0.5) | Array::range(0., 10., 0.5) | create a 1-D array with values 0., 0.5, …, 9.5 |
| np.linspace(0., 10., 11) | Array::linspace(0., 10., 11) | create a 1-D array with 11 elements with values 0., …, 10. |
| np.logspace(2.0, 3.0, num=4, base=10.0) | Array::logspace(10.0, 2.0, 3.0, 4) | create a 1-D array with 4 logarithmically spaced elements with values 100., 215.4, 464.1, 1000. |
| np.geomspace(1., 1000., num=4) | Array::geomspace(1e0, 1e3, 4) | create a 1-D array with 4 geometrically spaced elements from 1 to 1,000 inclusive: 1., 10., 100., 1000. |
| np.ones((3, 4, 5)) | Array::ones((3, 4, 5)) | create a 3×4×5 array filled with ones (inferring the element type) |
| np.zeros((3, 4, 5)) | Array::zeros((3, 4, 5)) | create a 3×4×5 array filled with zeros (inferring the element type) |
| np.zeros((3, 4, 5), order='F') | Array::zeros((3, 4, 5).f()) | create a 3×4×5 array with Fortran (column-major) memory layout filled with zeros (inferring the element type) |
| np.zeros_like(a, order='C') | Array::zeros(a.raw_dim()) | create an array of zeros of the shape shape as a, with row-major memory layout (unlike NumPy, this infers the element type from context instead of duplicating a’s element type) |
| np.full((3, 4), 7.) | Array::from_elem((3, 4), 7.) | create a 3×4 array filled with the value 7. |
| np.array([1, 2, 3, 4]).reshape((2, 2)) | Array::from_shape_vec((2, 2), vec![1, 2, 3, 4])? or .into_shape((2,2).unwrap() | create a 2×2 array from the elements in the Vec |
#![allow(unused)] fn main() { let a:Array<f64, Ix1> = Array::linspace(0., 4.5, 10); println!("{:?}", a); let b:Array<f64, _> = a.into_shape((2,5)).unwrap(); println!("\n{:?}", b); let c:Array<f64, _> = Array::zeros((3,4).f()); println!("\n{:?}", c); }
[4, 5, 6]]
[0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5], shape=[10], strides=[1], layout=CFcf (0xf), const ndim=1
[[0.0, 0.5, 1.0, 1.5, 2.0],
[2.5, 3.0, 3.5, 4.0, 4.5]], shape=[2, 5], strides=[5, 1], layout=Cc (0x5), const ndim=2
Good overview at this TDS Post, but subscription required.
#![allow(unused)] fn main() { :dep ndarray = { version = "^0.15.6" } // Not working on Jupyter notebook //:dep ndarray-rand = { version = "^0.15.0" } use ndarray::{Array, ShapeBuilder}; // Not working on Jupyter notebook //use ndarray_rand::RandomExt; //use ndarray_rand::rand_distr::Uniform; // Ones let ones = Array::<f64, _>::ones((1, 4)); println!("{:?}", ones); // Output: // [[1.0, 1.0, 1.0, 1.0]], shape=[1, 4], strides=[4, 1], layout=CFcf (0xf), const ndim=2 // Range let range = Array::<f64, _>::range(0., 5., 1.); println!("{:?}", range); // Output: // [0.0, 1.0, 2.0, 3.0, 4.0], shape=[5], strides=[1], layout=CFcf (0xf), const ndim=1 // Linspace let linspace = Array::<f64, _>::linspace(0., 5., 5); println!("{:?}", linspace); // Output: // [0.0, 1.25, 2.5, 3.75, 5.0], shape=[5], strides=[1], layout=CFcf (0xf), const ndim=1 // Fill let mut ones = Array::<f64, _>::ones((1, 4)); ones.fill(0.); println!("{:?}", ones); // Output: // [[0.0, 0.0, 0.0, 0.0]], shape=[1, 4], strides=[4, 1], layout=CFcf (0xf), const ndim=2 // Eye -- Identity Matrix let eye = Array::<f64, _>::eye(4); println!("{:?}", eye); // Output: // [[1.0, 0.0, 0.0, 0.0], // [0.0, 1.0, 0.0, 0.0], // [0.0, 0.0, 1.0, 0.0], // [0.0, 0.0, 0.0, 1.0]], shape=[4, 4], strides=[4, 1], layout=Cc (0x5), const ndim=2 // Random // Not working on Jupyter notebook //let random = Array::random((2, 5), Uniform::new(0., 10.)); //println!("{:?}", random); // Output: // [[9.375493735188611, 4.088737328406999, 9.778579742815943, 0.5225866490310649, 1.518053969762827], // [9.860829919571666, 2.9473768443117, 7.768332993584486, 7.163926861520167, 9.814750664983297]], shape=[2, 5], strides=[5, 1], layout=Cc (0x5), const ndim=2 }
[[0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0]], shape=[3, 4], strides=[1, 3], layout=Ff (0xa), const ndim=2
[[1.0, 1.0, 1.0, 1.0]], shape=[1, 4], strides=[4, 1], layout=CFcf (0xf), const ndim=2
[0.0, 1.0, 2.0, 3.0, 4.0], shape=[5], strides=[1], layout=CFcf (0xf), const ndim=1
[0.0, 1.25, 2.5, 3.75, 5.0], shape=[5], strides=[1], layout=CFcf (0xf), const ndim=1
What does the printout mean?
- The values of the array
- The shape of the array, most important dimension first
- The stride (always 1 for arrays in the last dimension, but can be different for views)
- The layout (storage order, view order)
- The number of dimensions
Indexing and Slicing
| NumPy | ndarray | Notes |
|---|---|---|
| a[-1] | a[a.len() - 1] | access the last element in 1-D array a |
| a[1, 4] | a[[1, 4]] | access the element in row 1, column 4 |
| a[1] or a[1, :, :] | a.slice(s![1, .., ..]) or a.index_axis(Axis(0), 1) | get a 2-D subview of a 3-D array at index 1 of axis 0 |
| a[0:5] or a[:5] or a[0:5, :] | a.slice(s![0..5, ..]) or a.slice(s![..5, ..]) or a.slice_axis(Axis(0), Slice::from(0..5)) | get the first 5 rows of a 2-D array |
| a[-5:] or a[-5:, :] | a.slice(s![-5.., ..]) or a.slice_axis(Axis(0), Slice::from(-5..)) | get the last 5 rows of a 2-D array |
| a[:3, 4:9] | a.slice(s![..3, 4..9]) | columns 4, 5, 6, 7, and 8 of the first 3 rows |
| a[1:4:2, ::-1] | a.slice(s![1..4;2, ..;-1]) | rows 1 and 3 with the columns in reverse order |
The s![] slice macro
-
The
s![]macro in Rust's ndarray crate is a convenient way to create slice specifications for array operations. -
It's used to create a
SliceInfoobject that describes how to slice or view an array.
Here's how it works:
- The
s![]macro is used to create slice specifications that are similar to Python's slice notation - It's commonly used with methods like
slice(),slice_mut(), and other array view operations - Inside the macro, you can specify ranges and steps for each dimension
For example:
#![allow(unused)] fn main() { let mut slice = array.slice_mut(s![1.., 0, ..]); }
This creates a slice that:
- Takes all elements from index 1 onwards in the first dimension (
1..) - Takes only index 0 in the second dimension (
0) - Takes all elements in the third dimension (
..)
The syntax inside s![] supports several patterns:
..- take all elements in that dimensionstart..end- take elements from start (inclusive) to end (exclusive)start..=end- take elements from start (inclusive) to end (inclusive)start..- take elements from start (inclusive) to the end..end- take elements from the beginning to end (exclusive)index- take only that specific index
For example:
#![allow(unused)] fn main() { // Take every other element in the first dimension s![..;2] // Take elements 1 to 3 in the first dimension, all elements in the second s![1..4, ..] // Take elements from index 2 to the end, with step size 2 s![2..;2] // Take specific indices s![1, 2, 3] }

From TDS Post.
#![allow(unused)] fn main() { use ndarray::{s}; { // Create a 3-dimensional array (2x3x4) let mut array = Array::from_shape_fn((2, 3, 4), |(i, j, k)| { (i * 100 + j * 10 + k) as f32 }); // Print the original 3-dimensional array println!("Original 3D array:\n{:?}", array); // Create a 2-dimensional slice (taking the first 2D layer) let mut slice = array.slice_mut(s![1.., 0, ..]); // Print the 2-dimensional slice println!("2D slice:\n{:?}", slice); // Create a 1-dimensional slice (taking the first 2D and 3D layer) let slice2 = array.slice(s![1, 0, ..]); // Print the 1-dimensional slice println!("1D slice:\n{:?}", slice2); } }
[[0.0, 0.0, 0.0, 0.0]], shape=[1, 4], strides=[4, 1], layout=CFcf (0xf), const ndim=2
[[1.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]], shape=[4, 4], strides=[4, 1], layout=Cc (0x5), const ndim=2
Original 3D array:
[[[0.0, 1.0, 2.0, 3.0],
[10.0, 11.0, 12.0, 13.0],
[20.0, 21.0, 22.0, 23.0]],
[[100.0, 101.0, 102.0, 103.0],
[110.0, 111.0, 112.0, 113.0],
[120.0, 121.0, 122.0, 123.0]]], shape=[2, 3, 4], strides=[12, 4, 1], layout=Cc (0x5), const ndim=3
2D slice:
[[100.0, 101.0, 102.0, 103.0]], shape=[1, 4], strides=[0, 1], layout=CFcf (0xf), const ndim=2
1D slice:
[100.0, 101.0, 102.0, 103.0], shape=[4], strides=[1], layout=CFcf (0xf), const ndim=1
()
2D and 3D datatypes, again from TDS Post.
#![allow(unused)] fn main() { use ndarray::{array, Array, Array2, Array3, ShapeBuilder}; // 1D array let array_d1 = Array::from_vec(vec![1., 2., 3., 4.]); println!("{:?}", array_d1); // Output: // [1.0, 2.0, 3.0, 4.0], shape=[4], strides=[1], layout=CFcf (0xf), const ndim=1 // or let array_d11 = Array::from_shape_vec((1, 4), vec![1., 2., 3., 4.]); println!("{:?}", array_d11.unwrap()); // Output: // [[1.0, 2.0, 3.0, 4.0]], shape=[1, 4], strides=[4, 1], layout=CFcf (0xf), const ndim=2 // 2D array let array_d2 = array![ [-1.01, 0.86, -4.60, 3.31, -4.81], [ 3.98, 0.53, -7.04, 5.29, 3.55], [ 3.30, 8.26, -3.89, 8.20, -1.51], [ 4.43, 4.96, -7.66, -7.33, 6.18], [ 7.31, -6.43, -6.16, 2.47, 5.58], ]; // or let array_d2 = Array::from_shape_vec((2, 2), vec![1., 2., 3., 4.]); println!("{:?}", array_d2.unwrap()); // Output: // [[1.0, 2.0], // [3.0, 4.0]], shape=[2, 2], strides=[2, 1], layout=Cc (0x5), const ndim=2 // or let mut data = vec![1., 2., 3., 4.]; let array_d21 = Array2::from_shape_vec((2, 2), data); // 3D array let mut data = vec![1., 2., 3., 4.]; let array_d3 = Array3::from_shape_vec((2, 2, 1), data); println!("{:?}", array_d3); // Output: // [[[1.0], // [2.0]], // [[3.0], // [4.0]]], shape=[2, 2, 1], strides=[2, 1, 1], layout=Cc (0x5), const ndim=3 }
[1.0, 2.0, 3.0, 4.0], shape=[4], strides=[1], layout=CFcf (0xf), const ndim=1
[[1.0, 2.0, 3.0, 4.0]], shape=[1, 4], strides=[4, 1], layout=CFcf (0xf), const ndim=2
[[1.0, 2.0],
[3.0, 4.0]], shape=[2, 2], strides=[2, 1], layout=Cc (0x5), const ndim=2
Reshaping

From TDS Post.

From TDS Post.
Examining the array parameters
| NumPy | ndarray | Notes |
|---|---|---|
| np.ndim(a) or a.ndim | a.ndim() | get the number of dimensions of array a |
| np.size(a) or a.size | a.len() | get the number of elements in array a |
| np.shape(a) or a.shape | a.shape() or a.dim() | get the shape of array a |
| a.shape[axis] | a.len_of(Axis(axis)) | get the length of an axis |
| a.strides | a.strides() | get the strides of array a |
| np.size(a) == 0 or a.size == 0 | a.is_empty() | check if the array has zero elements |
Simple Math
| NumPy | ndarray | Notes |
|---|---|---|
| a.transpose() or a.T | a.t() or a.reversed_axes() | transpose of array a (view for .t() or by-move for .reversed_axes()) |
| mat1.dot(mat2) | mat1.dot(&mat2) | 2-D matrix multiply |
| mat.dot(vec) | mat.dot(&vec) | 2-D matrix dot 1-D column vector |
| vec.dot(mat) | vec.dot(&mat) | 1-D row vector dot 2-D matrix |
| vec1.dot(vec2) | vec1.dot(&vec2) | vector dot product |
| a * b, a + b, etc. | a * b, a + b, etc. | element-wise arithmetic operations |
| a**3 | a.mapv(|a| a.powi(3)) | element-wise power of 3 |
| np.sqrt(a) | a.mapv(f64::sqrt) | element-wise square root for f64 array |
| (a>0.5) | a.mapv(|a| a > 0.5) | array of bools of same shape as a with true where a > 0.5 and false elsewhere |
| np.sum(a) or a.sum() | a.sum() | sum the elements in a |
| np.sum(a, axis=2) or a.sum(axis=2) | a.sum_axis(Axis(2)) | sum the elements in a along axis 2 |
| np.mean(a) or a.mean() | a.mean().unwrap() | calculate the mean of the elements in f64 array a |
| np.mean(a, axis=2) or a.mean(axis=2) | a.mean_axis(Axis(2)) | calculate the mean of the elements in a along axis 2 |
| np.allclose(a, b, atol=1e-8) | a.abs_diff_eq(&b, 1e-8) | check if the arrays’ elementwise differences are within an absolute tolerance (it requires the approx feature-flag) |
| np.diag(a) | a.diag() | view the diagonal of a |
mapv vs map:
mapv iterates over the values of the array, map iterates over mutable references of the array
Array-n
Array0 to Array6 also defined in addition to Array as special cases with fixed dimensions instead dynamically defined dimensions.
#![allow(unused)] fn main() { { // Create a 2-dimensional array (3x4) let mut a = Array::from_shape_fn((3, 4), |(j, k)| { (j * 10 + k) as f32 }); // Print the original 2-dimensional array println!("Original 2D array:\n{:?}", a); let b = a * 2.0; println!("\nb:\n{:?}", b); let c = b.mapv(|v| v>24.8); println!("\nc:\n{:?}", c); } }
Ok([[[1.0],
[2.0]],
[[3.0],
[4.0]]], shape=[2, 2, 1], strides=[2, 1, 1], layout=Cc (0x5), const ndim=3)
Original 2D array:
[[0.0, 1.0, 2.0, 3.0],
[10.0, 11.0, 12.0, 13.0],
[20.0, 21.0, 22.0, 23.0]], shape=[3, 4], strides=[4, 1], layout=Cc (0x5), const ndim=2
b:
[[0.0, 2.0, 4.0, 6.0],
[20.0, 22.0, 24.0, 26.0],
[40.0, 42.0, 44.0, 46.0]], shape=[3, 4], strides=[4, 1], layout=Cc (0x5), const ndim=2
c:
[[false, false, false, false],
[false, false, false, true],
[true, true, true, true]], shape=[3, 4], strides=[4, 1], layout=Cc (0x5), const ndim=2
()
Type Conversions
- std::convert::From ensures lossless, safe conversions at compile-time and is generally recommended.
- std::convert::TryFrom can be used for potentially unsafe conversions. It will return a Result which can be handled or unwrap()ed to panic if any value at runtime cannot be converted losslessly.
| NumPy | ndarray | Notes |
|---|---|---|
| a.astype(np.float32) | a.mapv(|x| f32::from(x)) | convert array to f32. Only use if can't fail |
| a.astype(np.int32) | a.mapv(|x| i32::from(x)) | convert array to i32. Only use if can't fail |
| a.astype(np.uint8) | a.mapv(|x| u8::try_from(x).unwrap()) | try to convert to u8 array, panic if any value cannot be converted lossless at runtime (e.g. negative value) |
| a.astype(np.int32) | a.mapv(|x| x as i32) | convert to i32 array with “saturating” conversion; care needed because it can be a lossy conversion or result in non-finite values! |
Basic Linear Algebra
Provided by NDArray.
Transpose

#![allow(unused)] fn main() { let array_d2 = Array::from_shape_vec((2, 2), vec![1., 2., 3., 4.]); println!("{:?}", array_d2.unwrap()); // Output // [[1.0, 2.0], // [3.0, 4.0]], shape=[2, 2], strides=[2, 1], layout=Cc (0x5), const ndim=2) let binding = array_d2.expect("Expect 2d matrix"); let array_d2t = binding.t(); println!("{:?}", array_d2t); // Output // [[1.0, 3.0], // [2.0, 4.0]], shape=[2, 2], strides=[1, 2], layout=Ff (0xa), const ndim=2 }
[E0382] Error: use of moved value: `array_d2`
╭─[command_8:1:1]
│
1 │ let array_d2 = Array::from_shape_vec((2, 2), vec![1., 2., 3., 4.]);
│ ────┬───
│ ╰───── move occurs because `array_d2` has type `Result<ndarray::ArrayBase<OwnedRepr<f64>, ndarray::Dim<[usize; 2]>>, ShapeError>`, which does not implement the `Copy` trait
2 │ println!("{:?}", array_d2.unwrap());
│ ────┬───│────┬───
│ ╰────────────── help: consider calling `.as_ref()` or `.as_mut()` to borrow the type's contents
│ │ │
│ ╰────────── help: you can `clone` the value and consume it, but this might not be your desired behavior: `.clone()`
│ │
│ ╰───── `array_d2` moved due to this method call
│
8 │ let binding = array_d2.expect("Expect 2d matrix");
│ ────┬───
│ ╰───── value used here after move
│
│ Note: note: `Result::<T, E>::unwrap` takes ownership of the receiver `self`, which moves `array_d2`
───╯
[E0597] Error: `binding` does not live long enough
╭─[command_8:1:1]
│
8 │ let binding = array_d2.expect("Expect 2d matrix");
│ ───┬───
│ ╰───── binding `binding` declared here
│
10 │ let array_d2t = binding.t();
│ ───┬─┬─────
│ ╰───────── borrowed value does not live long enough
│ │
│ ╰─────── argument requires that `binding` is borrowed for `'static`
────╯
Matrix Multiplication
#![allow(unused)] fn main() { use ndarray::{array, Array2}; let a: Array2<f64> = array![[3., 2.], [2., -2.]]; let b: Array2<f64> = array![[3., 2.], [2., -2.]]; let c = a.dot(&b); print!("{:?}", c); // Output // [[13.0, 2.0], // [2.0, 8.0]], shape=[2, 2], strides=[2, 1], layout=Cc (0x5), const ndim=2 }
[[13.0, 2.0],
Linear Algebra with ndarray-linalg
-
The crate
ndarray-linalgimplements more advanced lineary algebra operations that comes withNDArray. -
It relies on a native linear algebra library like
OpenBLASand can be tricky to configure. -
We show it here just for reference.
| NumPy | ndarray | Notes |
|---|---|---|
| numpy.linalg.inv(a) | a.inv() | Invert matrix a. Must be square |
| numpy.linalg.eig(a) | a.eig() | Compute eigenvalues and eigenvectors of matrix. Must be square |
| numpy.linalg.svd(a) | a.svd(true, true) | Compute the Singular Value Decomposition of matrix |
| numpy.linalg.det(a) | a.det() | Compute the determinant of a matrix. Must be square |
#![allow(unused)] fn main() { //```rust :dep ndarray = { version = "^0.15" } // This is the MAC version // See ./README.md for setup instructions :dep ndarray-linalg = { version = "^0.16", features = ["openblas-system"] } // This is the linux verison //:dep ndarray-linalg = { version = "^0.15", features = ["openblas"] } use ndarray::array; use ndarray_linalg::*; { // Create a 2D square matrix (3x3) let matrix = array![ [1.0, 2.0, 3.0], [0.0, 1.0, 4.0], [5.0, 6.0, 0.0] ]; // Compute the eigenvalues and eigenvectors match matrix.eig() { Ok((eigenvalues, eigenvectors)) => { println!("Eigenvalues:\n{:?}", eigenvalues); println!("Eigenvectors:\n{:?}", eigenvectors); }, Err(e) => println!("Failed to compute eigenvalues and eigenvectors: {:?}", e), } } //``` }
[2.0, 8.0]], shape=[2, 2], strides=[2, 1], layout=Cc (0x5), const ndim=2EVCXR_VARIABLE_CHANGED_TYPE:b
The type of the variable b was redefined, so was lost.
The type of the variable array_d21 was redefined, so was lost.
The type of the variable array_d3 was redefined, so was lost.
The type of the variable a was redefined, so was lost.
The type of the variable range was redefined, so was lost.
The type of the variable eye was redefined, so was lost.
The type of the variable c was redefined, so was lost.
The type of the variable array_d1 was redefined, so was lost.
The type of the variable linspace was redefined, so was lost.
The type of the variable ones was redefined, so was lost.
The type of the variable b was redefined, so was lost.
Eigenvalues:
[Complex { re: 7.256022422687388, im: 0.0 }, Complex { re: -0.026352822204034426, im: 0.0 }, Complex { re: -5.229669600483354, im: 0.0 }], shape=[3], strides=[1], layout=CFcf (0xf), const ndim=1
Eigenvectors:
[[Complex { re: -0.4992701697014973, im: 0.0 }, Complex { re: -0.7576983872742932, im: 0.0 }, Complex { re: -0.22578016277159085, im: 0.0 }],
[Complex { re: -0.4667420094775666, im: 0.0 }, Complex { re: 0.6321277120502754, im: 0.0 }, Complex { re: -0.526348454767688, im: 0.0 }],
[Complex { re: -0.7299871192254567, im: 0.0 }, Complex { re: -0.162196515314045, im: 0.0 }, Complex { re: 0.8197442419819131, im: 0.0 }]], shape=[3, 3], strides=[1, 3], layout=Ff (0xa), const ndim=2
()
The same code is provided as a cargo project.
Python Numpy Reference
For reference you can look at mnist_fcn.ipynb which implements and trains the network with only numpy matrices, but does use PyTorch dataset loaders for conciseness.
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Deriving and Implementing Traits: Debug and Display
About This Module
This module explores the #[derive(Debug)] attribute in detail and introduces manual
trait implementations. Understanding how derive macros work and when to implement
traits manually is important for creating user-friendly and debuggable Rust programs.
Prework
Prework Readings
Read the following sections from "The Rust Programming Language" book:
- Chapter 10.2: Traits: Defining Shared Behavior - Introduction only
- Chapter 19.5: Macros - Focus on derive macros
- Appendix C: Derivable Traits
Pre-lecture Reflections
Before class, consider these questions:
- What is the difference between
DebugandDisplayformatting? - Why might you want to manually implement a trait instead of using derive?
- How do derive macros help reduce boilerplate code?
- When would custom formatting be important for user experience?
- What role do traits play in Rust's type system?
Lecture
Learning Objectives
By the end of this module, you should be able to:
- Understand what
#[derive(Debug)]does under the hood - Manually implement the
Debugtrait for custom types - Implement the
Displaytrait for user-friendly output - Choose between
DebugandDisplayformatting appropriately - Understand when to use derive vs. manual implementation
- Apply formatting traits to make code more debuggable
Understanding #[derive(Debug)]
- A simple way to tell Rust to generate code that allows a complex type to be printed
- Here's the equivalent manual implementation of the
Debugtrait - more on traits and
impllater
use std::fmt;
impl fmt::Debug for Direction {
fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
match *self {
Direction::North => write!(f, "North"),
Direction::East => write!(f, "East"),
Direction::South => write!(f, "South"),
Direction::West => write!(f, "West"),
}
}
}
let dir = Direction::North;
dir
North
let dir = Direction::North;
println!("{:?}",dir);
North
// Example of how make a complex datatype printable directly (without deriving from Debug)
use std::fmt;
impl fmt::Display for Direction {
fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
match *self {
Direction::North => write!(f, "North"),
Direction::East => write!(f, "East"),
Direction::South => write!(f, "South"),
Direction::West => write!(f, "West"),
}
}
}
println!("{}", dir);
North
Best Practices
Design Guidelines:
#![allow(unused)] fn main() { #[derive(Debug, Clone, PartialEq)] pub enum UserAction { Login(String), Logout, UpdateProfile { name: String, email: String }, } impl fmt::Display for UserAction { fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result { match self { UserAction::Login(username) => write!(f, "User '{}' logged in", username), UserAction::Logout => write!(f, "User logged out"), UserAction::UpdateProfile { name, .. } => { write!(f, "User '{}' updated profile", name) } } } } // Usage let action = UserAction::Login("alice".to_string()); println!("{}", action); // User-friendly: "User 'alice' logged in" println!("{:?}", action); // Debug: Login("alice") }
When to Implement Manually:
- Security: Hide sensitive information in debug output
- Performance: Optimize formatting for frequently-used types
- User Experience: Create polished output for end users
- Domain Requirements: Follow domain-specific formatting conventions
Styles of Parallel Programming
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
- Instruction level parallelism (ILP)
- Done at the hardware level. CPU determines independent instructions and executes them in parallel! Often assisted by the compiler which arranges instruction so contiguous instructions can be executed concurrently.
- Single Instruction Multiple Data (SIMD)
- Done at the hardware level. A processor may be able to do, e.g., 1 Multiply-Accumulate of Int32, but 2 MACs per cycle for Int16 and 4 MACs per cycle of Int8.
- Thread level parallelism
- Done at the software level. Programmer or compiler decomposes program onto mostly independent parts and creates separate threads to execute them.
- Message passing between threads
- When coordination or data exchange needs arise in #3 the coordination and or data exchange happens by explicitly sending messages between threads.
- Shared memory between threads
- Threads share all the memory and use locks/barriers to coordinate between them (more below).
- Pipeline Parallelism
- Output of one thread is input to another
- Data parallelism
- Each thread works on a different part of the data
- Model parallelism (new)
- Arose due to large ML models where each thread/core has a part of the model and updates its parameters
Rust language supports thread level parallelism primitives.
We'll look at three of them (3.1, 3.2, 3.3 ) and mention the other briefly (3.4).
Processor Scaling and Multicore Architectures
In 1965, Gordon Moore, cofounder of Intel, observed that component count of processors was doubling about every 2 years.
He predicted that it would continue for at least the next 10 years.
This became known as "Moore's Law".
In fact it has held up for over 50 years.
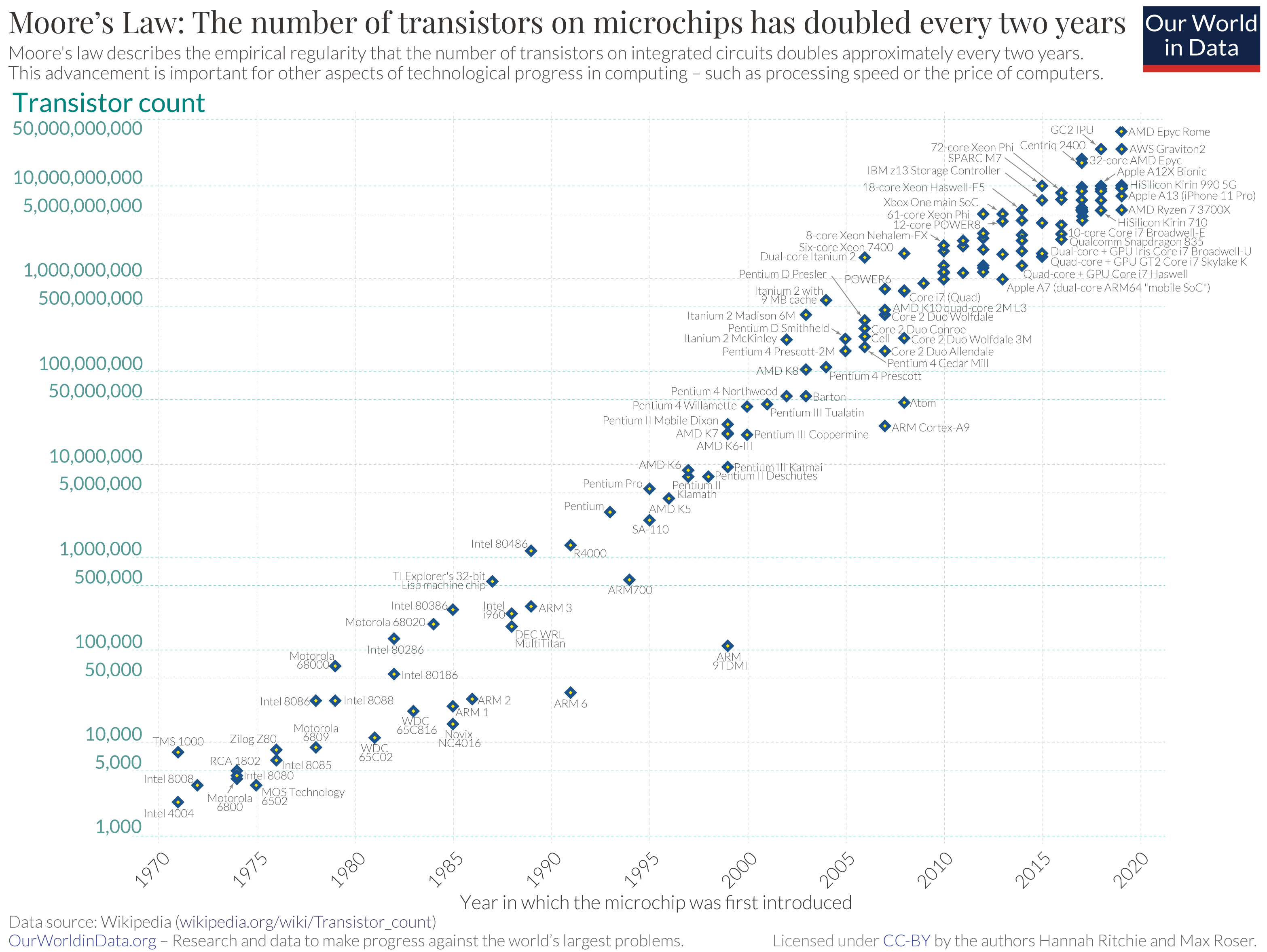
The industry did this by shrinking component size, which also allowed to increase the clock rate.
Up to a point...
Became increasingly difficult to continue to grow the transistor count...
And increasingly difficult to improve single core performance.
The alternative was to start putting more cores in the processor.
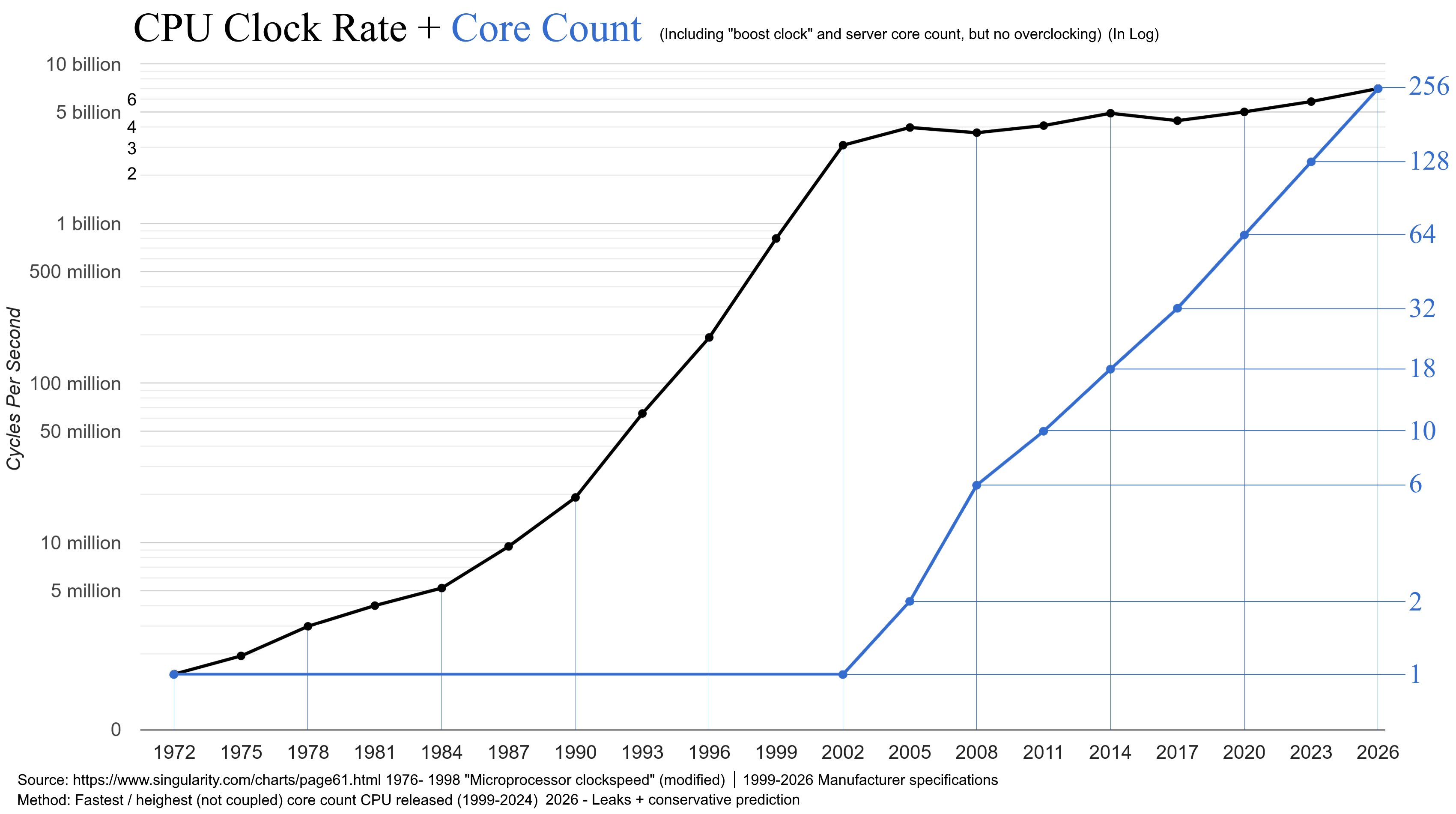

How much memory in a NVDA A100 GPU?
- 80 Gbytes of high bandwidth memory
What is the size of GPT-4?
- 1.7 trillion parameters, at 4 bytes each, 6.8 TBytes
- 1.7 trillion parameters, at 2 bytes each, 3.4 TBytes
- So clearly it will not fit in a single GPU memory
2. Limits of Parallel Programming
Let an algorithm A have a serial S and a parallel P part. Then the time to execute G is:
Running on multiple processors only affects
which as becomes
So the maximum possible speedup for a program is
3. Rust Parallel and Concurrent Programming
It helps to look at what constitutes a CPU core and a thread.
Intel processors have typically supported 2 threads/core.
New Mac processors typically support 1 hardware thread/core.
But the OS can support many more SW threads (thousands).
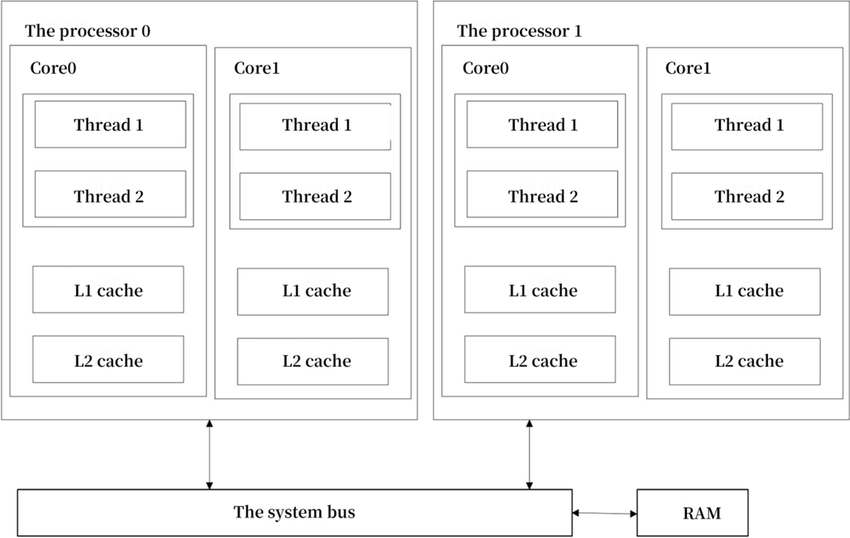
Rust libraries provide constructs for different types of parallel/concurrent programming.
- Threads (
spawn,join) - Message Passing Via Channels (
mpsc) - Shared Memory/State Concurrency using Mutexes (
mutex) - Asynchronous Programing with
Async, Await, Futures, ... Rust Lang §17
3.1 Using Threads in Rust
Examples from Rust Language Book, §16.1.
Rust let's you manually assign program code to additional threads.
Let's "spawn" a thread and print a statement 10 times with a 1 millisecond sleep between iterations.
use std::thread; use std::time::Duration; fn main(){ thread::spawn(|| { for i in 1..10 { println!("hi number {i} from the spawned thread!"); thread::sleep(Duration::from_millis(1)); } }); for i in 1..5 { println!("hi number {i} from the main thread!"); thread::sleep(Duration::from_millis(1)); } } main();
hi number 1 from the main thread!
hi number 1 from the spawned thread!
hi number 2 from the main thread!
hi number 2 from the spawned thread!
hi number 3 from the main thread!
hi number 3 from the spawned thread!
hi number 4 from the main thread!
hi number 4 from the spawned thread!
hi number 5 from the spawned thread!
Why did we not complete the print loop in the thread?
The main thread completed and the program shut down.
We can wait till the other thread completes using join handles.
use std::thread; use std::time::Duration; fn main() { // get a handle to the thread let handle = thread::spawn(|| { for i in 1..10 { println!("hi number {i} from the spawned thread!"); thread::sleep(Duration::from_millis(1)); } }); for i in 1..5 { println!("hi number {i} from the main thread!"); thread::sleep(Duration::from_millis(1)); } handle.join().unwrap(); } main();
hi number 1 from the main thread!
hi number 1 from the spawned thread!
hi number 2 from the main thread!
hi number 2 from the spawned thread!
hi number 3 from the spawned thread!
hi number 3 from the main thread!
hi number 4 from the spawned thread!
hi number 4 from the main thread!
hi number 5 from the spawned thread!
hi number 6 from the spawned thread!
hi number 7 from the spawned thread!
hi number 8 from the spawned thread!
hi number 9 from the spawned thread!
What if we want to use variables from the our main thread in the spawned thread?
#![allow(unused)] fn main() { use std::thread; { let v = vec![1, 2, 3]; let handle = thread::spawn( || { println!("Here's a vector: {v:?}"); }); handle.join().unwrap(); } }
[E0373] Error: closure may outlive the current function, but it borrows `v`, which is owned by the current function
╭─[command_10:1:1]
│
6 │ ╭─▶ let handle = thread::spawn( || {
│ │ ┬┬
│ │ ╰─── help: to force the closure to take ownership of `v` (and any other referenced variables), use the `move` keyword: `move `
│ │ │
│ │ ╰── may outlive borrowed value `v`
7 │ │ println!("Here's a vector: {v:?}");
│ │ ┬
│ │ ╰── `v` is borrowed here
8 │ ├─▶ });
│ │
│ ╰───────────── note: function requires argument type to outlive `'static`
───╯
The Rust compiler won't let us borrow from a spawned thread.
We have to use the move directive.
#![allow(unused)] fn main() { use std::thread; { let v = vec![1, 2, 3]; let handle = thread::spawn(move || { println!("Here's a vector: {v:?}"); }); handle.join().unwrap(); } }
Here's a vector: [1, 2, 3]
()
3.2 Using Message Passing
So we spawned threads that can act completely independently.
What if we need communication or coordination between threads?
One popular pattern in many languages is message passing.
Message passing via channels.
Each channel has a Transmitter (tx) and Reciever (Rx).
std::sync::mpsc -- Multiple Producer, Single Consumer
Example with single producer, single consumer.
#![allow(unused)] fn main() { use std::sync::mpsc; use std::thread; { let (tx, rx) = mpsc::channel(); thread::spawn(move || { let val = String::from("hi"); tx.send(val).unwrap(); }); let received = rx.recv().unwrap(); println!("Got: {received}"); } }
Got: hi
()
Reminder that the
unwrap()
method works on the Result enum in that if the Result is Ok, it will produce the value inside the Ok. If the Result is the Err variant, unwrap will call the panic! macro.
Example with Multiple Producer, Single Consumer.
#![allow(unused)] fn main() { use std::sync::mpsc; use std::thread; use std::time::Duration; { let (tx, rx) = mpsc::channel(); let tx1 = tx.clone(); thread::spawn(move || { let vals = vec![ String::from("hi"), String::from("from"), String::from("the"), String::from("thread"), ]; for val in vals { tx1.send(val).unwrap(); thread::sleep(Duration::from_secs(1)); } }); thread::spawn(move || { let vals = vec![ String::from("more"), String::from("messages"), String::from("for"), String::from("you"), ]; for val in vals { tx.send(val).unwrap(); thread::sleep(Duration::from_secs(1)); } }); for received in rx { println!("Got: {received}"); } } }
Got: hi
Got: more
Got: messages
Got: from
Got: for
Got: the
Got: you
Got: thread
()
3.3 Shared Memory/State Concurrency
The other approach for coordinating between threads is to use shared memory with a mutually exclusive (Mutex) lock on the memory.
#![allow(unused)] fn main() { use std::sync::Mutex; { let m = Mutex::new(5); { let mut num = m.lock().unwrap(); // to access the data we have to lock it *num = 6; } // the lock released at the end of the scope println!("m = {m:?}"); } }
m = Mutex { data: 6, poisoned: false, .. }
()
What if we wanted multiple threads to increment the same counter.
We have to use Atomic Reference Counting (Arc).
#![allow(unused)] fn main() { use std::sync::{Arc, Mutex}; use std::thread; { let counter = Arc::new(Mutex::new(0)); // Create an Arc on a Mutex of int32 let mut handles = vec![]; for _ in 0..10 { let counter = Arc::clone(&counter); // Use Arc::clone() method let handle = thread::spawn(move || { let mut num = counter.lock().unwrap(); // lock the counter mutex to increment it *num += 1; }); // mutex is unlocked at end of scope handles.push(handle); } for handle in handles { handle.join().unwrap(); } println!("Result: {}", *counter.lock().unwrap()); } }
Result: 10
()
3.4 Asynchronous Programming: Async, Await, Futures, etc.
This material is optional.
Rust (and other languages) have language constructs that abstracts away the particulars of managing and coordinating threads.
You can use Rust's asynchronous programming features (see Rust Book, Ch. 17) to describe which parts of your program can execute asynchronously and how to express dependency points between them.

Mixed parallel and concurrent workflow. Fig 17-3 from the Rust Book.
From Futures and the Async Syntax:
-
A future is a value that may not be ready now but will become ready at some point in the future.
-
You can apply the
asynckeyword to blocks and functions to specify that they can be interrupted and resumed. -
Within an async block or async function, you can use the
awaitkeyword to await a future- that is, wait for it to become ready.
-
Any point where you await a future within an async block or function is a potential spot for that async block or function to pause and resume.
-
The process of checking with a future to see if its value is available yet is called polling.
See Rust Book, Ch. 17 to dive deeper.
Additional Examples (Optional)
Message passing between threads
- The code demonstrates thread communication using Rust's
mpsc(multiple producer, single consumer) channels to exchange messages between threads. - Two worker threads are spawned, each with its own pair of channels for bidirectional communication with the main thread.
- The main thread coordinates the communication by receiving messages from both worker threads and sending responses back to them.
- The code uses thread synchronization primitives like
join()to ensure proper thread termination andsleep()to manage timing.
use std::thread; use std::sync::mpsc; use std::time::Duration; fn communicate(id:i32, tx: mpsc::Sender<String>, rx:mpsc::Receiver<&str>) { let t = format!("Hello from thread {}", id); tx.send(t).unwrap(); let a:&str = rx.recv().unwrap(); println!("Thread {} received {}", id, a); } fn main_thread() { let (tx1, rx1) = mpsc::channel(); let (tx2, rx2) = mpsc::channel(); // let handle1 = let handle1 = thread::spawn(move || { communicate(1, tx1, rx2); }); let (tx3, rx3) = mpsc::channel(); let (tx4, rx4) = mpsc::channel(); // let handle2 = let handle2 = thread::spawn(move || { communicate(2, tx3, rx4); }); let a:String = rx1.recv().unwrap(); let b:String = rx3.recv().unwrap(); println!("Main thread got \n{}\n{}\n\n", a, b); tx2.send("Hi from main").unwrap(); tx4.send("Hi from main").unwrap(); thread::sleep(Duration::from_millis(5000)); handle1.join().unwrap(); handle2.join().unwrap(); } main_thread();
Main thread got
Hello from thread 1
Hello from thread 2
Thread 1 received Hi from main
Thread 2 received Hi from main
More example programs
Summarized by ChatGPT.
These are posted to https://github.com/trgardos/ds210-b1-sp25-lectures/tree/main/lecture_24_optional_code.
- Creates a configurable square matrix (default 64x64) and processes it in parallel using Rust's Rayon library
- Divides the matrix into chunks based on the number of specified threads, with each thread processing its assigned chunk
- Uses Rayon's
scopeandspawnfunctions for parallel execution, where each thread writes its ID number to its assigned matrix section - Includes options to configure matrix size, number of threads, and display the matrix before/after processing
- The program demonstrates parallel matrix processing with configurable parameters (matrix size, thread count, and synchronization method) using command-line arguments
- It implements three different synchronization approaches:
- Exclusive locking using
Mutex - Reader-only access using
RwLockread locks - Writer access using
RwLockwrite locks
- Exclusive locking using
- The program uses Rust's concurrency primitives:
Arcfor thread-safe shared ownershipMutexandRwLockfor synchronizationthread::spawnfor parallel execution
- Each thread processes a segment of the matrix, calculates a sum, and the program measures and reports the total execution time
- Implements parallel Gaussian elimination using Rayon's parallel iterators (
par_iter_mut) for both matrix initialization and row elimination operations - Uses thread-safe random number generation with ChaCha8Rng, where each thread gets its own seeded RNG instance
- Allows configuration of matrix size and number of threads via command-line arguments
- Includes performance timing measurements and optional matrix display functionality
- Implements Conway's Game of Life simulation with parallel processing using Rayon's concurrency primitives (
scopeandspawn) - Divides the board into chunks that are processed concurrently by multiple threads, with each thread handling a specific section of the board
- Uses command-line arguments to control simulation parameters (board size, thread count, display options, iteration count, and delay between iterations)
- Includes a glider pattern initialization and visual rendering of the board state, with timing measurements for performance analysis
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Calling Rust from Python
Content regarding how to write performant python modules in Rust.
Prework
We'll be using PyO3 and the maturin python module.
Either follow the maturin tutorial or one of the examples from PyO3 Using Rust from Python.
This TDS blog could be helpful.
Prework Assessment
A short assessment of the prework material to check and reinforce students' understanding and readiness for the lecture.
Lecture
Recap of the prework material, perhaps in a bit more depth and additional examples.
Technical Coding Challenge
Introduce and discuss the technical coding challenge where the solution can be implemented with material and language syntax learned so far.
Coding Challenge
Students work on the coding challenge in groups of 3 and submit their solutions online.
Coding Challenge Review
Review the coding challenge in class:
- peer review of solutions with comments... maybe randomly select 3 other students to do the review
- instructor randomly select a group to present their solution
File Input/Output in Rust
About This Module
This module covers file input/output operations in Rust, focusing on reading from and writing to files safely and efficiently. Students will learn how to handle files, work with the std::fs and std::io modules, and implement error handling for file operations. The module includes practical examples of reading and writing different data formats, with a focus on processing large datasets commonly used in data science applications.
Prework
Before this lecture, please read:
- The Rust Book Chapter 12.1: "Accepting Command Line Arguments" - https://doc.rust-lang.org/book/ch12-01-accepting-command-line-arguments.html
- The Rust Book Chapter 9: "Error Handling" - https://doc.rust-lang.org/book/ch09-00-error-handling.html
- The Rust Book Chapter 12.3: "Refining the Library with Tests" - https://doc.rust-lang.org/book/ch12-03-improving-error-handling-and-modularity.html (focus on file I/O sections)
Pre-lecture Reflections
- How does Rust's ownership model affect file handling compared to other languages?
- What are the advantages of Rust's
Resulttype for file I/O error handling? - When would you use buffered vs. unbuffered file reading in data processing applications?
Lecture
Learning Objectives
By the end of this lecture, you should be able to:
- Open, read from, and write to files in Rust using
std::fsandstd::io - Handle file I/O errors properly using
Resulttypes andexpect() - Use buffered readers for efficient file processing
- Parse and generate file formats commonly used in data science
- Implement file-based data processing workflows
File I/O
See also file_io.
:dep rand="0.8.5"
use std::fs::File; // object providing access to an open file on filesystem
use std::io::prelude::*; // imports common I/O traits
use rand::Rng;
fn generate_file(path: &str, n: usize) {
// Generate a random file of edges for vertices 0.n
// Create a file at `path` and return Result<File> or error
// .expect() unwraps the Result<File> or prints error and panics
let mut file = File::create(path).expect("Unable to create file");
for i in 0..n {
// How many neighbors will this node have
let rng = rand::thread_rng().gen_range(0..20) as usize;
for _j in 0..rng {
// Randomly select a neighbor (even with duplicates but not to ourselves)
let neighbor = rand::thread_rng().gen_range(0..n) as usize;
if neighbor != i {
let s: String = format!("{} {}\n", i, neighbor);
file.write_all(s.as_bytes()).expect("Unable to write file");
}
}
}
}
fn read_file(path: &str) -> Vec<(u32, u32)> {
let mut result: Vec<(u32, u32)> = Vec::new();
let file = File::open(path).expect("Could not open file");
let buf_reader = std::io::BufReader::new(file).lines();
for line in buf_reader {
let line_str = line.expect("Error reading");
let v: Vec<&str> = line_str.trim().split(' ').collect();
let x = v[0].parse::<u32>().unwrap();
let y = v[1].parse::<u32>().unwrap();
result.push((x, y));
}
return result;
}
println!("Generating file");
generate_file("list_of_edges.txt", 10);
let edges = read_file("list_of_edges.txt");
println!("{:?}", edges);
Generating file
[(0, 5), (0, 9), (0, 1), (0, 8), (0, 2), (0, 2), (0, 1), (0, 6), (0, 8), (0, 9), (1, 6), (1, 6), (1, 4), (2, 7), (2, 7), (2, 1), (2, 1), (2, 8), (2, 6), (3, 0), (3, 1), (3, 2), (3, 8), (3, 2), (3, 8), (3, 0), (3, 4), (3, 8), (3, 7), (3, 8), (3, 0), (3, 8), (3, 2), (3, 6), (3, 8), (3, 4), (4, 7), (4, 2), (4, 0), (4, 5), (4, 0), (4, 9), (4, 2), (4, 2), (4, 9), (4, 7), (4, 3), (4, 9), (4, 9), (5, 8), (5, 0), (5, 3), (5, 4), (5, 2), (5, 4), (5, 9), (6, 3), (6, 7), (6, 9), (6, 3), (6, 7), (6, 7), (6, 4), (6, 0), (6, 3), (6, 8), (6, 0), (6, 9), (6, 5), (7, 4), (7, 9), (7, 3), (7, 6), (7, 3), (7, 9), (7, 1), (7, 8), (7, 1), (7, 2), (7, 2), (8, 2), (8, 0), (8, 1), (8, 3), (8, 7), (8, 5), (8, 4), (9, 2), (9, 3), (9, 4), (9, 5), (9, 4), (9, 2), (9, 5), (9, 2)]NDArray and Neural networks
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
-
Simple neural networks can be easily represented by matrix arithmentic.
-
Let's see how we can build a relatively simple neural network to recognize handwritten digits.
Biological Neuron
An _artificial neuron_is loosely modeled on a biological neuron.

From Stanford's cs231n
- The dendrites carry impulses from other neurons of different distances.
- Once the collective firing rate of the impulses exceed a certain threshold, the neuron fires its own pulse through the axon to other neurons.
Artificial Neuron
The artificial neuron is loosely based on the biological one.

From Stanford's cs231n.
The artifical neuron:
- collects one or more inputs,
- each multiplied by a unique weight,
- sums the weighted inputs,
- adds a bias,
- then applies a nonlinear activation function.
Multi-Layer Perceptron (MLP) or Fully Connected Network (FCN)

From Stanford's cs231n.
-
Multiple artificial neurons can act on the same inputs,. This defines a layer. We can have more than one layer until we produce one or more outputs.
-
The example above shows a network with 3 inputs, two layers of neurons, each with 4 neurons, followed by one layer that produces a single value output.
This architecture can be used as a binary classifier.
FCN Detailed View
Here's a more detailed view of a fully connected network making biases explicit and with weight matrix and bias vector dimensions

We can collect all the inputs into a column vector.
Then we can gather the weights for the first layer:
where is a nonlinear activation function, such as ReLU shown below.

The equation for which is.
or in pseudocode simply:
x = max(0, x)
The nonlinear activation functions are crucial, because without them, the neural network can be simplified down to a single linear system of equations, which is severely limited in its representational power.
The subsequent layers can be defined similarly interms of the activations of the previous activation functions.
where the last function is a softmax, which limits the output to between 0 and 1, and all the outputs sum up to 1.
Here's a visualization.

From TDS Post.
Much of neural network training and evaluation comes down to vector operations in which ndarray excels.
Training a Neural Network
-
We won't go into all the details of training a network, but we'll show an example.
-
The steps involve producing the outpur from some input -- Forward Pass
-
Then updating the weights and biases of the network, taking the partial derivatives of the entire model with respect to each parameter and then updating each parameter proportional to its partial derivative -- Backward Pass
Simple weight update example
We'll build our understanding of the gradient by considering derivatives of single variable functions.
Let's start with a quadratic function
The derivative with respect to of our example is
This is the asymptotic slope at any particular value of .

Question: Which way does need to move at to decrease ? Positive or negative direction?
Question: What about at ? Positive or negative direction?
An easy way to update this is:
where is some small number (e.g. 0.01) which we call the learning rate.
Minimizing the Network Loss
To train our network we want to minize some function that computes the difference between our target values and what the network produces for each input .
An appropriate loss function for classification models is the categorical cross-entropy loss.
The following image from the Medium Post illustrates the full pipeline:

except in the figure is the model output and are the targets.
We won't go into details but a nice output is that
Forward propagation
-
Weights would be represented by an
Array2<f32>with dimensions: (# neurons # inputs)- For example if you have 100 input neurons and 50 2nd layer neurons then you need a matrix of weights
-
Bias vectors would be represented by an
Array2<f32>with dimensions (# neurons 1)
Backwards propagation
-
As mentioned, in practice the calculation of partial derivatives must be calculated starting with the end of the pipeline and then working backwards.
-
The chain rule for differentiation in calculus gives a modular, scalable way of doing this calculation, again starting from the end and working backwards.
Just a reminder, we have
We already did
And the process continues.
Example Implementaiton
Let's look at an example implementation.
We'll start with some utility functions.
#![allow(unused)] fn main() { :dep ndarray = { version = "^0.15" } :dep rand = { version = "0.8" } use ndarray::prelude::*; use rand::Rng; // Helper function to populate arrays with random values // We could use ndarray-rand crate to do this, but it doesn't seem to work in a Jupyter notebook fn populate_array(arr: &mut Array2<f32>, m: usize, n: usize) { let mut rng = rand::thread_rng(); for i in 0..m { for j in 0..n { arr[(i, j)] = rng.gen_range(-1.0..1.0); } } } // ReLU activation function fn relu(x: &Array2<f32>) -> Array2<f32> { x.mapv(|x| if x > 0.0 { x } else { 0.0 }) } // Derivative of ReLU fn relu_derivative(x: &Array2<f32>) -> Array2<f32> { x.mapv(|x| if x > 0.0 { 1.0 } else { 0.0 }) } // Softmax function fn softmax(x: &Array2<f32>) -> Array2<f32> { let exp_x = x.mapv(|x| x.exp()); let sum_exp_x = exp_x.sum(); exp_x / sum_exp_x } }
Then we'll define a NeuralNetwork struct and associated methods.
#![allow(unused)] fn main() { struct NeuralNetwork { input_size: usize, output_size: usize, weights1: Array2<f32>, biases1: Array2<f32>, weights2: Array2<f32>, biases2: Array2<f32>, learning_rate: f32, } impl NeuralNetwork { /// Create a shallow neural network with one hidden layer /// /// # Arguments /// /// * `input_size` - The number of input neurons /// * `hidden_size` - The number of neurons in the hidden layer /// * `output_size` - The number of output neurons /// * `learning_rate` - The learning rate for the neural network fn new(input_size: usize, hidden_size: usize, output_size: usize, learning_rate: f32) -> Self { let mut weights1 = Array2::zeros((hidden_size, input_size)); let mut weights2 = Array2::zeros((output_size, hidden_size)); // Initialize weights with random values populate_array(&mut weights1, hidden_size, input_size); populate_array(&mut weights2, output_size, hidden_size); let biases1 = Array2::zeros((hidden_size, 1)); let biases2 = Array2::zeros((output_size, 1)); NeuralNetwork { input_size, output_size, weights1, biases1, weights2, biases2, learning_rate, } } fn forward(&self, input: &Array2<f32>) -> (Array2<f32>, Array2<f32>, Array2<f32>) { // First layer let pre_activation1 = self.weights1.dot(input) + &self.biases1; let hidden = relu(&pre_activation1); // Output layer let pre_activation2 = self.weights2.dot(&hidden) + &self.biases2; let output = softmax(&pre_activation2); (hidden, pre_activation2, output) } fn backward( &mut self, input: &Array2<f32>, hidden: &Array2<f32>, pre_activation2: &Array2<f32>, output: &Array2<f32>, target: &Array2<f32>, ) { let batch_size = input.shape()[1] as f32; // Calculate gradients for output layer let output_error = output - target; // Gradients for weights2 and biases2 let d_weights2 = output_error.dot(&hidden.t()) / batch_size; let d_biases2 = &output_error.sum_axis(Axis(1)).insert_axis(Axis(1)) / batch_size; // Backpropagate error to hidden layer let hidden_error = self.weights2.t().dot(&output_error); let hidden_gradient = &hidden_error * &relu_derivative(hidden); // Gradients for weights1 and biases1 let d_weights1 = hidden_gradient.dot(&input.t()) / batch_size; let d_biases1 = &hidden_gradient.sum_axis(Axis(1)).insert_axis(Axis(1)) / batch_size; // Update weights and biases using gradient descent self.weights2 = &self.weights2 - &(d_weights2 * self.learning_rate); self.biases2 = &self.biases2 - &(d_biases2 * self.learning_rate); self.weights1 = &self.weights1 - &(d_weights1 * self.learning_rate); self.biases1 = &self.biases1 - &(d_biases1 * self.learning_rate); } fn train(&mut self, input: &Array2<f32>, target: &Array2<f32>) -> f32 { // Forward pass let (hidden, pre_activation2, output) = self.forward(input); // Calculate loss (cross-entropy) let epsilon = 1e-15; let loss = -target * &output.mapv(|x| (x + epsilon).ln()); let loss = loss.sum() / (input.shape()[1] as f32); // Backward pass self.backward(input, &hidden, &pre_activation2, &output, target); loss } } }
fn main() { // Create a neural network let mut nn = NeuralNetwork::new(6, 6, 4, 0.01); // Create sample input let mut input = Array2::zeros((nn.input_size, 1)); populate_array(&mut input, nn.input_size, 1); // Create sample target let mut target = Array2::zeros((nn.output_size, 1)); populate_array(&mut target, nn.output_size, 1); // Calculate initial cross entropy loss before training let (_, _, initial_output) = nn.forward(&input); let epsilon = 1e-15; let initial_loss = -&target * &initial_output.mapv(|x| (x + epsilon).ln()); let initial_loss = initial_loss.sum() / (input.shape()[1] as f32); println!("Initial loss before training: {}", initial_loss); // Train for one iteration let loss = nn.train(&input, &target); //println!("Loss: {}", loss); // Calculate loss after training let (_, _, final_output) = nn.forward(&input); let epsilon = 1e-15; let final_loss = -&target * &final_output.mapv(|x| (x + epsilon).ln()); let final_loss = final_loss.sum() / (input.shape()[1] as f32); println!("loss after training: {}", final_loss); }
We can now run an iteration of a forward pass and backward pass.
You can repeatedly run this cell to see the loss decreasing.
#![allow(unused)] fn main() { main() }
Initial loss before training: 1.5886599
loss after training: 1.5812341
()
Has anyone implemented neural networks in Rust?
See for example candle. Perhaps a pun on "Torch" from "PyTorch".
But the point isn't to use an existing package but learn how to build a simple one from basic linear algebra principles.
All of this and more...
- Quick start: https://github.com/rust-ndarray/ndarray/blob/master/README-quick-start.md
- Numpy equivalence: https://docs.rs/ndarray/latest/ndarray/doc/ndarray_for_numpy_users/index.html
- Linear Algebra: https://github.com/rust-ndarray/ndarray-linalg/blob/master/README.md
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Plotters -- Rust Drawing Library
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
From the website:
Plotters is a drawing library designed for rendering figures, plots, and charts, in pure Rust.
Full documentation is at https://docs.rs/plotters/latest/plotters/.
Installation and Configuration
Rust Project
In Cargo.toml add the following dependency
[dependencies]
plotters="0.3.6"
Or inside Jupyter notebook
For 2021 edition:
:dep plotters = { version = "^0.3.6", default_features = false, features = ["evcxr", "all_series"] }
For 2024 edition, default_features became default-features (dash instead of underscore):
:dep plotters = { version = "^0.3.6", default-features = false, features = ["evcxr", "all_series"] }
Plotters Tutorial
We'll go through the interactive tutorial, reproduced here.
Import everything defined in prelude which includes evcxr_figure().
// Rust 2021 edition syntax
//:dep plotters = { version = "^0.3.6", default_features = false, features = ["evcxr", "all_series"] }
// Rust 2024 edition syntax: changed the syntax to 'default-feature'
:dep plotters = { version = "^0.3.6", default-features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
// Import all the plotters prelude functions
use plotters::prelude::*;
// To create a figure that can be displayed in Jupyter notebook, use evcxr_figure function.
// The first param is the resolution of the figure.
// The second param is the closure that performes the drawing.
evcxr_figure((300, 100), |name| {
// Do the drawings
name.fill(&BLUE)?;
// Tell plotters that everything is ok
Ok(())
})
evcxr_figure((xsize, ysize), |name| { your code })is how you make a figure of a certain size and put things in it.- name is the handle for accessing the figure
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((320,50), |root| {
root.fill(&GREEN)?;
root.draw(&Text::new("Hello World from Plotters!", (15, 15), ("Arial", 20).into_font()))?;
Ok(())
})
Sub-Drawing Areas
The object created by evcxr_figure is a DrawingArea
DrawingArea is a key concept and represents the handle into which things will be actually drawn. Plotters supports different types of drawing areas depending on context.
- Inside jupyter notebook the type of drawing area is an SVG (Scalable Vector Graphics) area
- When used from the termina the most common type is a BitMapBackend
For full documentation on what you can do with DrawingArea see https://docs.rs/plotters/latest/plotters/drawing/struct.DrawingArea.html
Key capabilities:
- fill: Fill it with a background color
- draw_mesh: Draw a mesh on it
- draw_text: Add some text in graphic form
- present: make it visible (may not be neeed in all backend types)
- titled: Add a title and return the remaining area
- split_*: Split it into subareas in a variety of ways
Split Drawing Areas Example
We can make a Sierpiński carpet by splitting the drawing areas and recursion function.
The Sierpiński carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions...
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
use plotters::coord::Shift;
pub fn sierpinski_carpet(
depth: u32,
drawing_area: &DrawingArea<SVGBackend, Shift>) -> Result<(), Box<dyn std::error::Error>> {
if depth > 0 {
// Split the drawing area into 9 equal parts
let sub_areas = drawing_area.split_evenly((3,3));
// Iterate over the sub-areas
for (idx, sub_area) in (0..).zip(sub_areas.iter()) {
if idx == 4 { // idx == 4 is the center sub-area
// If the sub-area is the center one, fill it with white
sub_area.fill(&WHITE)?;
} else {
sierpinski_carpet(depth - 1, sub_area)?;
}
}
}
Ok(())
}
evcxr_figure((480,480), |root| {
root.fill(&BLACK)?;
sierpinski_carpet(5, &root)
}).style("width: 600px") /* You can add CSS style to the result */
/* Note: doesn't work in VSCode/Cursor */
Charts
Drawing areas are too basic for scientific drawings so the next important concept is a chart
Charts can be used to plot functions, datasets, bargraphs, scatterplots, 3D Objects and other stuff.
Full documentation at https://docs.rs/plotters/latest/plotters/chart/struct.ChartBuilder.html and https://docs.rs/plotters/latest/plotters/chart/struct.ChartContext.html
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((640, 240), |root| {
// The following code will create a chart context
let mut chart = ChartBuilder::on(&root)
// the caption for the chart
.caption("Hello Plotters Chart Context!", ("Arial", 20).into_font())
// the X and Y coordinates spaces for the chart
.build_cartesian_2d(0f32..1f32, 0f32..1f32)?;
// Then we can draw a series on it!
chart.draw_series((1..10).map(|x|{
let x = x as f32/10.0;
Circle::new((x,x), 5, &RED)
}))?;
Ok(())
}).style("width:60%")
Common chart components
Adding a mesh, and X and Y labels
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
// The following code will create a chart context
let mut chart = ChartBuilder::on(&root)
.caption("Chart with Axis Label", ("Arial", 20).into_font())
.x_label_area_size(80)
.y_label_area_size(80)
.build_cartesian_2d(0f32..1f32, 0f32..1f32)?;
chart.configure_mesh()
.x_desc("Here's the label for X")
.y_desc("Here's the label for Y")
.draw()?;
// Then we can draw a series on it!
chart.draw_series((1..10).map(|x|{
let x = x as f32/10.0;
Circle::new((x,x), 5, &RED)
}))?;
Ok(())
}).style("width: 60%")
Then let's disable mesh lines for the X axis
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
// The following code will create a chart context
let mut chart = ChartBuilder::on(&root)
.caption("Chart Context with Mesh and Axis", ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(0f32..1f32, 0f32..1f32)?;
chart.configure_mesh()
.y_labels(10)
.light_line_style(&TRANSPARENT)
.disable_x_mesh()
.draw()?;
// Then we can draw a series on it!
chart.draw_series((1..10).map(|x|{
let x = x as f32/10.0;
Circle::new((x,x), 5, &RED)
}))?;
Ok(())
}).style("width: 60%")
Adding subcharts
Simple. Split your drawing area and then add a chart in each of the split portions
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
let sub_areas = root.split_evenly((2,2));
for (idx, area) in (1..).zip(sub_areas.iter()) {
// The following code will create a chart context
let mut chart = ChartBuilder::on(&area)
.caption(format!("Subchart #{}", idx), ("Arial", 15).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(0f32..1f32, 0f32..1f32)?;
chart.configure_mesh()
.y_labels(10)
.light_line_style(&TRANSPARENT)
.disable_x_mesh()
.draw()?;
// Then we can draw a series on it!
chart.draw_series((1..10).map(|x|{
let x = x as f32/10.0;
Circle::new((x,x), 5, &RED)
}))?;
}
Ok(())
}).style("width: 60%")
Drawing on Charts with the Series Abstraction
-
Unlike most of the plotting libraries,
Plottersdoesn't actually define any types of chart. -
All the charts are abstracted to a concept of series.
- By doing so, you can put a histgoram series and a line plot series into the same chart context.
-
The series is actually defined as an iterator of elements.
This gives Plotters a huge flexibility on drawing charts. You can implement your own types of series and uses the coordinate translation and chart elements.
There are few types of predefined series, just for convenience:
- Line Series
- Histogram
- Point Series
Scatter Plot
First, generate random numbers
:dep rand = { version = "0.6.5" }
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate rand;
use rand::distributions::Normal;
use rand::distributions::Distribution;
use rand::thread_rng;
let sd = 0.13;
let random_points:Vec<(f64,f64)> = {
let mut norm_dist = Normal::new(0.5, sd);
let (mut x_rand, mut y_rand) = (thread_rng(), thread_rng());
let x_iter = norm_dist.sample_iter(&mut x_rand);
let y_iter = norm_dist.sample_iter(&mut y_rand);
x_iter.zip(y_iter).take(1000).collect()
};
println!("{}", random_points.len());
1000
To draw the series, we provide an iterator on the elements and then map a closure.
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((480, 480), |root| {
// The following code will create a chart context
let mut chart = ChartBuilder::on(&root)
.caption("Normal Distribution w/ 2 sigma", ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
.build_ranged(0f64..1f64, 0f64..1f64)?;
chart.configure_mesh()
.disable_x_mesh()
.disable_y_mesh()
.draw()?;
// Draw little green circles. Remember that closures can capture variables from the enclosing scope
chart.draw_series(random_points.iter().map(|(x,y)| Circle::new((*x,*y), 3, GREEN.filled())));
// You can always freely draw on the drawing backend. So we can add background after the fact
let area = chart.plotting_area();
let two_sigma = sd * 2.0;
let chart_width = 480;
let radius = two_sigma * chart_width as f64; // circle radius is in pixels not chart coords
area.draw(&Circle::new((0.5, 0.5), radius, RED.mix(0.3).filled()))?;
area.draw(&Cross::new((0.5, 0.5), 5, &RED))?;
Ok(())
}).style("width:60%")
Histograms
We can also have histograms. For histograms, we can use the predefined histogram series struct to build the histogram easily. The following code demonstrate how to create both histogram for X and Y value of random_points.
// Rust 2021
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series", "all_elements"] }
// Rust 2024
:dep plotters = { version = "^0.3.0", default-features = false, features = ["evcxr", "all_series", "all_elements"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
let areas = root.split_evenly((2,1));
let mut charts = vec![];
// The following code will create a chart context
for (area, name) in areas.iter().zip(["X", "Y"].into_iter()) {
let mut chart = ChartBuilder::on(&area)
.caption(format!("Histogram for {}", name), ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(0u32..100u32, 0f64..0.5f64)?;
chart.configure_mesh()
.disable_x_mesh()
.disable_y_mesh()
.y_labels(5)
.x_label_formatter(&|x| format!("{:.1}", *x as f64 / 100.0))
.y_label_formatter(&|y| format!("{}%", (*y * 100.0) as u32))
.draw()?;
charts.push(chart);
}
// Histogram is just another series but a nicely encapsulated one
let hist_x = Histogram::vertical(&charts[0])
.style(RED.filled())
.margin(0)
.data(random_points.iter().map(|(x,_)| ((x*100.0) as u32, 0.01)));
let hist_y = Histogram::vertical(&charts[0])
.style(GREEN.filled())
.margin(0)
.data(random_points.iter().map(|(_,y)| ((y*100.0) as u32, 0.01)));
charts[0].draw_series(hist_x);
charts[1].draw_series(hist_y);
Ok(())
}).style("width:60%")
Fancy combination of histogram and scatter
Split the drawing area in 3 parts and draw two histograms and a scatter plot
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series", "all_elements"] }
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
let root = root.titled("Scatter with Histogram Example", ("Arial", 20).into_font())?;
// Split the drawing area into a grid with specified X and Y breakpoints
let areas = root.split_by_breakpoints([560], [80]);
let mut x_hist_ctx = ChartBuilder::on(&areas[0])
.y_label_area_size(40)
.build_cartesian_2d(0u32..100u32, 0f64..0.5f64)?;
let mut y_hist_ctx = ChartBuilder::on(&areas[3])
.x_label_area_size(40)
.build_cartesian_2d(0f64..0.5f64, 0..100u32)?;
let mut scatter_ctx = ChartBuilder::on(&areas[2])
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(0f64..1f64, 0f64..1f64)?;
scatter_ctx.configure_mesh()
.disable_x_mesh()
.disable_y_mesh()
.draw()?;
scatter_ctx.draw_series(random_points.iter().map(|(x,y)| Circle::new((*x,*y), 3, GREEN.filled())))?;
let x_hist = Histogram::vertical(&x_hist_ctx)
.style(RED.filled())
.margin(0)
.data(random_points.iter().map(|(x,_)| ((x*100.0) as u32, 0.01)));
let y_hist = Histogram::horizontal(&y_hist_ctx)
.style(GREEN.filled())
.margin(0)
.data(random_points.iter().map(|(_,y)| ((y*100.0) as u32, 0.01)));
x_hist_ctx.draw_series(x_hist)?;
y_hist_ctx.draw_series(y_hist)?;
Ok(())
}).style("width:60%")
Drawing Lines
It's stil using the draw_series call with the convenient wrapper of LineSeries.
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series", "all_elements"] }
use plotters::prelude::*;
evcxr_figure((640, 480), |root_area| {
root_area.fill(&WHITE)?;
let root_area = root_area.titled("Line Graph", ("sans-serif", 60))?;
let x_axis = (-3.4f32..3.4).step(0.1);
let mut cc = ChartBuilder::on(&root_area)
.margin(5)
.set_all_label_area_size(50)
.caption("Sine and Cosine", ("sans-serif", 40))
.build_cartesian_2d(-3.4f32..3.4, -1.2f32..1.2f32)?;
cc.configure_mesh()
.x_labels(20)
.y_labels(10)
.disable_mesh()
.x_label_formatter(&|v| format!("{:.1}", v))
.y_label_formatter(&|v| format!("{:.1}", v))
.draw()?;
cc.draw_series(LineSeries::new(x_axis.values().map(|x| (x, x.sin())), &RED))?
.label("Sine")
.legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], RED));
cc.draw_series(LineSeries::new(x_axis.values().map(|x| (x, x.cos())), &BLUE,))?
.label("Cosine")
.legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], BLUE));
cc.configure_series_labels().border_style(BLACK).draw()?;
Ok(())
}).style("width:60%")
3D Plotting
Big difference is in the ChartBuilder call. Instead of build_cartesian_2d we use build_cartesian_3d.
Unlike the 2D plots, 3D plots use the function configure_axes to configure the chart components.
//:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series", "all_elements"] }
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
let root = root.titled("3D Plotting", ("Arial", 20).into_font())?;
let mut chart = ChartBuilder::on(&root)
.build_cartesian_3d(-10.0..10.0, -10.0..10.0, -10.0..10.0)?;
chart.configure_axes().draw()?;
// Draw a red circle parallel to XOZ panel
chart.draw_series(LineSeries::new(
(-314..314).map(|a| a as f64 / 100.0).map(|a| (8.0 * a.cos(), 0.0, 8.0 *a.sin())),
&RED,
))?;
// Draw a green circle parallel to YOZ panel
chart.draw_series(LineSeries::new(
(-314..314).map(|a| a as f64 / 100.0).map(|a| (0.0, 8.0 * a.cos(), 8.0 *a.sin())),
&GREEN,
))?;
Ok(())
})
For more examples check
https://plotters-rs.github.io/plotters-doc-data/evcxr-jupyter-integration.html
What about using it from the terminal?
The key difference is in how you define your drawing area.
-
Inside Jupyter notebook we create a drawing area using evcxr_figure
-
In the terminal context we create a drawing area using
#![allow(unused)] fn main() { let root = BitMapBackend::new("0.png", (640, 480)).into_drawing_area(); // or let root = SVGBackend::new("0.svg", (1024, 768)).into_drawing_area(); // or let root = BitMapBackend::gif("0.gif", (600, 400), 100)?.into_drawing_area(); }
Let's take a look on the terminal example (demo).
What if you don't want output to a file or a browser but standalone application?
Things get very messy and machine specific there. You need to integrate with the underlying OS graphics terminal libraries. For MacOS and Linux this is the the CairoBackend library but I don't know what it is for Windows
Here's an example from the terminal using GTK.
On MacOS, install these dependencies first:
brew install gtk4
brew install pkg-config
Then cargo run in (plotters-gtk-demo).
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
CSV Files and Basic Data Engineering
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
- Data Engineering in Rust
- Reading CSV Files
- Deserializing CSV Files
- Cleaning CSV Files
- Converting CSV Data to NDArray representation
- Reading CSV Files
- Deserializing CSV Files
- Cleaning CSV Files
- Converting CSV Data to NDArray representation
-
By default CSV will generate StringRecords which are structs containing an array of strings
-
Missing fields will be represented as empty strings
:dep csv = { version = "^1.3" }
let mut rdr = csv::Reader::from_path("uspop.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.records() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record = result.expect("a CSV record");
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
}
StringRecord(["Davidsons Landing", "AK", "", "65.2419444", "-165.2716667"])
StringRecord(["Kenai", "AK", "7610", "60.5544444", "-151.2583333"])
StringRecord(["Oakman", "AL", "", "33.7133333", "-87.3886111"])
StringRecord(["Richards Crossroads", "AL", "", "31.7369444", "-85.2644444"])
StringRecord(["Sandfort", "AL", "", "32.3380556", "-85.2233333"])
()
What if there malformed records with mismatched fields?
:dep csv = { version = "^1.3" }
let mut rdr = csv::Reader::from_path("usbad.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.records() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record = result.expect("a CSV record");
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
}
StringRecord(["Davidsons Landing", "AK", "", "65.2419444", "-165.2716667"])
StringRecord(["Kenai", "AK", "7610", "60.5544444", "-151.2583333"])
thread '<unnamed>' panicked at src/lib.rs:164:25:
a CSV record: Error(UnequalLengths { pos: Some(Position { byte: 125, line: 4, record: 3 }), expected_len: 5, len: 8 })
stack backtrace:
0: _rust_begin_unwind
1: core::panicking::panic_fmt
2: core::result::unwrap_failed
3: std::panic::catch_unwind
4: _run_user_code_16
5: evcxr::runtime::Runtime::run_loop
6: evcxr::runtime::runtime_hook
7: evcxr_jupyter::main
note: Some details are omitted, run with `RUST_BACKTRACE=full` for a verbose backtrace.
Let's make this safe for malformed records. Match statements to the rescue
:dep csv = { version = "^1.3" }
let mut rdr = csv::Reader::from_path("usbad.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.records() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
match result {
Ok(record) => {
if count < 5 {
println!("{:?}", record);
}
count += 1;
},
Err(err) => {
println!("error reading CSV record {}", err);
}
}
}
StringRecord(["Davidsons Landing", "AK", "", "65.2419444", "-165.2716667"])
StringRecord(["Kenai", "AK", "7610", "60.5544444", "-151.2583333"])
error reading CSV record CSV error: record 3 (line: 4, byte: 125): found record with 8 fields, but the previous record has 5 fields
StringRecord(["Kenai", "AK", "7610", "60.5544444", "-151.2583333"])
()
If your csv file has headers and you want to access them then you can use the headers function
By default, the first row is treated as a special header row.
:dep csv = { version = "^1.3" }
{
let mut rdr = csv::Reader::from_path("usbad.csv").unwrap();
let mut count = 0;
// Loop over each record.
let headers = rdr.headers()?;
println!("Headers: {:?}", headers);
for result in rdr.records() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
match result {
Ok(record) => {
if count < 5 {
println!("{:?}", record);
}
count += 1;
},
Err(err) => {
println!("error reading CSV record {}", err);
}
}
}
}
Headers: StringRecord(["City", "State", "Population", "Latitude", "Longitude"])
StringRecord(["Davidsons Landing", "AK", "", "65.2419444", "-165.2716667"])
StringRecord(["Kenai", "AK", "7610", "60.5544444", "-151.2583333"])
error reading CSV record CSV error: record 3 (line: 4, byte: 125): found record with 8 fields, but the previous record has 5 fields
StringRecord(["Kenai", "AK", "7610", "60.5544444", "-151.2583333"])
()
You can customize your reader in many ways:
#![allow(unused)] fn main() { let mut rdr = csv::ReaderBuilder::new() .has_headers(false) .delimiter(b';') .double_quote(false) .escape(Some(b'\\')) .flexible(true) .comment(Some(b'#')) .from_path("Some path"); }
What is the difference between a ReaderBuilder and a Reader? One is customizable and one is not.
2. Deserializing CSV Files
StringRecords are not particularly useful in computation. They typically have to be converted to floats or integers before we can work with them.
You can deserialize your CSV data either into a:
-
Record with types you define, or
-
a hashmap of key value pairs
Custom Record
:dep csv = { version = "^1.3" }
use std::collections::HashMap;
type StrRecord = (String, String, Option<u64>, f64, f64);
let mut rdr = csv::Reader::from_path("uspop.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:StrRecord = result.expect("a CSV record");
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
}
("Davidsons Landing", "AK", None, 65.2419444, -165.2716667)
("Kenai", "AK", Some(7610), 60.5544444, -151.2583333)
("Oakman", "AL", None, 33.7133333, -87.3886111)
("Richards Crossroads", "AL", None, 31.7369444, -85.2644444)
("Sandfort", "AL", None, 32.3380556, -85.2233333)
()
Note that we use
Option<T>on one of the types that we know has some empty values.
HashMap
Note the order of the outputs in print.
:dep csv = { version = "^1.3" }
use std::collections::HashMap;
type Record = HashMap<String, String>;
let mut rdr = csv::Reader::from_path("uspop.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:Record = result.expect("a CSV record");
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
}
{"State": "AK", "Latitude": "65.2419444", "Population": "", "City": "Davidsons Landing", "Longitude": "-165.2716667"}
{"Population": "7610", "City": "Kenai", "State": "AK", "Longitude": "-151.2583333", "Latitude": "60.5544444"}
{"Latitude": "33.7133333", "City": "Oakman", "Population": "", "Longitude": "-87.3886111", "State": "AL"}
{"Population": "", "Longitude": "-85.2644444", "City": "Richards Crossroads", "State": "AL", "Latitude": "31.7369444"}
{"City": "Sandfort", "Latitude": "32.3380556", "Longitude": "-85.2233333", "State": "AL", "Population": ""}
()
This will work well but makes it hard to read and know what type is associated with which CSV field
You can do better by using serde and structs
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)] // derive the Deserialize trait
#[serde(rename_all = "PascalCase")]
struct SerRecord {
latitude: f64,
longitude: f64,
population: Option<u64>, // account for the fact that some records have no population
city: String,
state: String,
}
let mut rdr = csv::Reader::from_path("uspop.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:SerRecord = result.expect("a CSV record");
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
}
The type of the variable rdr was redefined, so was lost.
SerRecord { latitude: 65.2419444, longitude: -165.2716667, population: None, city: "Davidsons Landing", state: "AK" }
SerRecord { latitude: 60.5544444, longitude: -151.2583333, population: Some(7610), city: "Kenai", state: "AK" }
SerRecord { latitude: 33.7133333, longitude: -87.3886111, population: None, city: "Oakman", state: "AL" }
SerRecord { latitude: 31.7369444, longitude: -85.2644444, population: None, city: "Richards Crossroads", state: "AL" }
SerRecord { latitude: 32.3380556, longitude: -85.2233333, population: None, city: "Sandfort", state: "AL" }
()
What about deserializing with invalid data?
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct FSerRecord {
latitude: f64,
longitude: f64,
population: Option<u64>,
city: String,
state: String,
}
let mut rdr = csv::Reader::from_path("usbad.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:FSerRecord = result.expect("a CSV record");
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
}
FSerRecord { latitude: 65.2419444, longitude: -165.2716667, population: None, city: "Davidsons Landing", state: "AK" }
FSerRecord { latitude: 60.5544444, longitude: -151.2583333, population: Some(7610), city: "Kenai", state: "AK" }
thread '<unnamed>' panicked at src/lib.rs:335:36:
a CSV record: Error(UnequalLengths { pos: Some(Position { byte: 125, line: 4, record: 3 }), expected_len: 5, len: 8 })
stack backtrace:
0: _rust_begin_unwind
1: core::panicking::panic_fmt
2: core::result::unwrap_failed
3: <unknown>
4: <unknown>
5: evcxr::runtime::Runtime::run_loop
6: evcxr::runtime::runtime_hook
7: evcxr_jupyter::main
note: Some details are omitted, run with `RUST_BACKTRACE=full` for a verbose backtrace.
Deserialization failed so we need to deal with bad records just like before. Match statement to the rescue
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct GSerRecord {
latitude: f64,
longitude: f64,
population: Option<u64>,
city: String,
state: String,
}
let mut rdr = csv::Reader::from_path("usbad.csv").unwrap();
let mut count = 0;
// Loop over each record.
// We need to specify the type we are deserializing to because compiler
// cannot infer the type from the match statement
for result in rdr.deserialize::<GSerRecord>() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
match result {
Ok(record) => {
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
},
Err(err) => {
println!("{}", err);
}
}
}
GSerRecord { latitude: 65.2419444, longitude: -165.2716667, population: None, city: "Davidsons Landing", state: "AK" }
GSerRecord { latitude: 60.5544444, longitude: -151.2583333, population: Some(7610), city: "Kenai", state: "AK" }
CSV error: record 3 (line: 4, byte: 125): found record with 8 fields, but the previous record has 5 fields
GSerRecord { latitude: 60.5544444, longitude: -151.2583333, population: Some(7610), city: "Kenai", state: "AK" }
()
Some more complex work. Let's filter cities over a population threshold
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct FilterRecord {
latitude: f64,
longitude: f64,
population: Option<u64>,
city: String,
state: String,
}
let mut rdr = csv::Reader::from_path("uspop.csv").unwrap();
let minimum_pop: u64 = 50_000;
// Loop over each record.
for result in rdr.deserialize::<FilterRecord>() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
match result {
Ok(record) => {
// `map_or` is a combinator on `Option`. It take two parameters:
// a value to use when the `Option` is `None` (i.e., the record has
// no population count) and a closure that returns another value of
// the same type when the `Option` is `Some`. In this case, we test it
// against our minimum population count that we got from the command
// line.
if record.population.map_or(false, |pop| pop >= minimum_pop) {
println!("{:?}", record);
}
},
Err(err) => {
println!("{}", err);
}
}
}
FilterRecord { latitude: 34.0738889, longitude: -117.3127778, population: Some(52335), city: "Colton", state: "CA" }
FilterRecord { latitude: 34.0922222, longitude: -117.4341667, population: Some(169160), city: "Fontana", state: "CA" }
FilterRecord { latitude: 33.7091667, longitude: -117.9527778, population: Some(56133), city: "Fountain Valley", state: "CA" }
FilterRecord { latitude: 37.4283333, longitude: -121.9055556, population: Some(62636), city: "Milpitas", state: "CA" }
FilterRecord { latitude: 33.4269444, longitude: -117.6111111, population: Some(62272), city: "San Clemente", state: "CA" }
FilterRecord { latitude: 41.1669444, longitude: -73.2052778, population: Some(139090), city: "Bridgeport", state: "CT" }
FilterRecord { latitude: 34.0230556, longitude: -84.3616667, population: Some(77218), city: "Roswell", state: "GA" }
FilterRecord { latitude: 39.7683333, longitude: -86.1580556, population: Some(773283), city: "Indianapolis", state: "IN" }
FilterRecord { latitude: 45.12, longitude: -93.2875, population: Some(62528), city: "Coon Rapids", state: "MN" }
FilterRecord { latitude: 40.6686111, longitude: -74.1147222, population: Some(59878), city: "Bayonne", state: "NJ" }
FilterRecord { latitude: 45.4983333, longitude: -122.4302778, population: Some(98851), city: "Gresham", state: "OR" }
FilterRecord { latitude: 34.9247222, longitude: -81.0252778, population: Some(59766), city: "Rock Hill", state: "SC" }
FilterRecord { latitude: 26.3013889, longitude: -98.1630556, population: Some(60509), city: "Edinburg", state: "TX" }
FilterRecord { latitude: 32.8369444, longitude: -97.0816667, population: Some(53221), city: "Euless", state: "TX" }
FilterRecord { latitude: 26.1944444, longitude: -98.1833333, population: Some(60687), city: "Pharr", state: "TX" }
()
Cleaning CSV Files
Once you have a Record you can push it to a vector and then iterate over the vector to fix it. Deserialization doesn't quite work all that well when the fields themselves are malformed
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct DirtyRecord {
CustomerNumber: Option<u32>,
CustomerName: String,
S2016: Option<f64>,
S2017: Option<f64>,
PercentGrowth: Option<f64>,
JanUnits:Option<u64>,
Month: Option<u8>,
Day: Option<u8>,
Year: Option<u16>,
Active: String,
}
let mut rdr = csv::Reader::from_path("sales_data_types.csv").unwrap();
let mut count = 0;
// Loop over each record.
for result in rdr.deserialize::<DirtyRecord>() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
match result {
Ok(record) => {
// Print a debug version of the record.
if count < 5 {
println!("{:?}", record);
}
count += 1;
},
Err(err) => {
println!("{}", err);
}
}
}
CSV deserialize error: record 1 (line: 2, byte: 85): field 0: invalid digit found in string
CSV deserialize error: record 2 (line: 3, byte: 161): field 2: invalid float literal
CSV deserialize error: record 3 (line: 4, byte: 236): field 2: invalid float literal
CSV deserialize error: record 4 (line: 5, byte: 305): field 2: invalid float literal
CSV deserialize error: record 5 (line: 6, byte: 370): field 2: invalid float literal
()
An alternative is to read everything as Strings and clean them up using String methods.
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct DirtyRecord {
CustomerNumber: String,
CustomerName: String,
S2016: String,
S2017: String,
PercentGrowth: String,
JanUnits:String,
Month: String,
Day: String,
Year: String,
Active: String,
}
#[derive(Debug, Default)]
struct CleanRecord {
CustomerNumber: u64,
CustomerName: String,
S2016: f64,
S2017: f64,
PercentGrowth: f32,
JanUnits:u64,
Month: u8,
Day: u8,
Year: u16,
Active: bool,
}
fn cleanRecord(r: DirtyRecord) -> CleanRecord {
let mut c = CleanRecord::default();
c.CustomerNumber = r.CustomerNumber.trim_matches('"').parse::<f64>().unwrap() as u64;
c.CustomerName = r.CustomerName.clone();
c.S2016 = r.S2016.replace('$',"").replace(',',"").parse::<f64>().unwrap();
c.S2017 = r.S2017.replace('$',"").replace(',',"").parse::<f64>().unwrap();
c.PercentGrowth = r.PercentGrowth.replace('%',"").parse::<f32>().unwrap() / 100.0;
let JanUnits = r.JanUnits.parse::<u64>();
if JanUnits.is_ok() {
c.JanUnits = JanUnits.unwrap();
} else {
c.JanUnits = 0;
}
c.Month = r.Month.parse::<u8>().unwrap();
c.Day = r.Day.parse::<u8>().unwrap();
c.Year = r.Year.parse::<u16>().unwrap();
c.Active = if r.Active == "Y" { true } else {false};
return c;
}
fn process_csv_file() -> Vec<CleanRecord> {
let mut rdr = csv::Reader::from_path("sales_data_types.csv").unwrap();
let mut v:Vec<DirtyRecord> = Vec::new();
// Loop over each record.
for result in rdr.deserialize::<DirtyRecord>() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
match result {
Ok(record) => {
// Print a debug version of the record.
println!("{:?}", record);
v.push(record);
},
Err(err) => {
println!("{}", err);
}
}
}
println!("");
let mut cleanv: Vec<CleanRecord> = Vec::new();
for r in v {
let cleanrec = cleanRecord(r);
println!("{:?}", cleanrec);
cleanv.push(cleanrec);
}
return cleanv;
}
process_csv_file();
DirtyRecord { CustomerNumber: "10002.0", CustomerName: "QuestIndustries", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">125</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>162500.00", PercentGrowth: "30.00%", JanUnits: "500", Month: "1", Day: "10", Year: "2015", Active: "Y" }
DirtyRecord { CustomerNumber: "552278", CustomerName: "SmithPlumbing", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">920</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>101,2000.00", PercentGrowth: "10.00%", JanUnits: "700", Month: "6", Day: "15", Year: "2014", Active: "Y" }
DirtyRecord { CustomerNumber: "23477", CustomerName: "ACMEIndustrial", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">50</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>62500.00", PercentGrowth: "25.00%", JanUnits: "125", Month: "3", Day: "29", Year: "2016", Active: "Y" }
DirtyRecord { CustomerNumber: "24900", CustomerName: "BrekkeLTD", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">350</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>490000.00", PercentGrowth: "4.00%", JanUnits: "75", Month: "10", Day: "27", Year: "2015", Active: "Y" }
DirtyRecord { CustomerNumber: "651029", CustomerName: "HarborCo", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">15</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>12750.00", PercentGrowth: "-15.00%", JanUnits: "Closed", Month: "2", Day: "2", Year: "2014", Active: "N" }
CleanRecord { CustomerNumber: 10002, CustomerName: "QuestIndustries", S2016: 125000.0, S2017: 162500.0, PercentGrowth: 0.3, JanUnits: 500, Month: 1, Day: 10, Year: 2015, Active: true }
CleanRecord { CustomerNumber: 552278, CustomerName: "SmithPlumbing", S2016: 920000.0, S2017: 1012000.0, PercentGrowth: 0.1, JanUnits: 700, Month: 6, Day: 15, Year: 2014, Active: true }
CleanRecord { CustomerNumber: 23477, CustomerName: "ACMEIndustrial", S2016: 50000.0, S2017: 62500.0, PercentGrowth: 0.25, JanUnits: 125, Month: 3, Day: 29, Year: 2016, Active: true }
CleanRecord { CustomerNumber: 24900, CustomerName: "BrekkeLTD", S2016: 350000.0, S2017: 490000.0, PercentGrowth: 0.04, JanUnits: 75, Month: 10, Day: 27, Year: 2015, Active: true }
CleanRecord { CustomerNumber: 651029, CustomerName: "HarborCo", S2016: 15000.0, S2017: 12750.0, PercentGrowth: -0.15, JanUnits: 0, Month: 2, Day: 2, Year: 2014, Active: false }
4. Let's convert the Vector of structs to an ndarray that can be fed into other libraries
Remember that ndarrays have to contain uniform data, so make sure the "columns" you pick are of the same type or you convert them appropriately.
:dep ndarray = { version = "^0.15.6" }
use ndarray::Array2;
let mut cleanv = process_csv_file();
let mut flat_values: Vec<f64> = Vec::new();
for s in &cleanv {
flat_values.push(s.S2016);
flat_values.push(s.S2017);
flat_values.push(s.PercentGrowth as f64);
}
let array = Array2::from_shape_vec((cleanv.len(), 3), flat_values).expect("Error creating ndarray");
println!("{:?}", array);
CleanRecord { CustomerNumber: 10002, CustomerName: "QuestIndustries", S2016: 125000.0, S2017: 162500.0, PercentGrowth: 0.3, JanUnits: 500, Month: 1, Day: 10, Year: 2015, Active: true }
CleanRecord { CustomerNumber: 552278, CustomerName: "SmithPlumbing", S2016: 920000.0, S2017: 1012000.0, PercentGrowth: 0.1, JanUnits: 700, Month: 6, Day: 15, Year: 2014, Active: true }
CleanRecord { CustomerNumber: 23477, CustomerName: "ACMEIndustrial", S2016: 50000.0, S2017: 62500.0, PercentGrowth: 0.25, JanUnits: 125, Month: 3, Day: 29, Year: 2016, Active: true }
CleanRecord { CustomerNumber: 24900, CustomerName: "BrekkeLTD", S2016: 350000.0, S2017: 490000.0, PercentGrowth: 0.04, JanUnits: 75, Month: 10, Day: 27, Year: 2015, Active: true }
CleanRecord { CustomerNumber: 651029, CustomerName: "HarborCo", S2016: 15000.0, S2017: 12750.0, PercentGrowth: -0.15, JanUnits: 0, Month: 2, Day: 2, Year: 2014, Active: false }
DirtyRecord { CustomerNumber: "10002.0", CustomerName: "QuestIndustries", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">125</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>162500.00", PercentGrowth: "30.00%", JanUnits: "500", Month: "1", Day: "10", Year: "2015", Active: "Y" }
DirtyRecord { CustomerNumber: "552278", CustomerName: "SmithPlumbing", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">920</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>101,2000.00", PercentGrowth: "10.00%", JanUnits: "700", Month: "6", Day: "15", Year: "2014", Active: "Y" }
DirtyRecord { CustomerNumber: "23477", CustomerName: "ACMEIndustrial", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">50</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>62500.00", PercentGrowth: "25.00%", JanUnits: "125", Month: "3", Day: "29", Year: "2016", Active: "Y" }
DirtyRecord { CustomerNumber: "24900", CustomerName: "BrekkeLTD", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">350</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>490000.00", PercentGrowth: "4.00%", JanUnits: "75", Month: "10", Day: "27", Year: "2015", Active: "Y" }
DirtyRecord { CustomerNumber: "651029", CustomerName: "HarborCo", S2016: "<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">15</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">000.00"</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">2017</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">"</span></span></span></span>12750.00", PercentGrowth: "-15.00%", JanUnits: "Closed", Month: "2", Day: "2", Year: "2014", Active: "N" }
If your data does not need cleaning
This is not likely, but sometimes data preprocessing happens in other environments and you are given a clean file to work with. Or you clean the data once and use it to train many different models. There is a crate that lets you go directly from csv to ndarray!
https://docs.rs/ndarray-csv/latest/ndarray_csv/
:dep csv = { version = "^1.3.1" }
:dep ndarray = { version = "^0.15.6" }
:dep ndarray-csv = { version = "^0.5.3" }
extern crate ndarray;
extern crate ndarray_csv;
use csv::{ReaderBuilder, WriterBuilder};
use ndarray::{array, Array2};
use ndarray_csv::{Array2Reader, Array2Writer};
use std::error::Error;
use std::fs::File;
fn main() -> Result<(), Box<dyn Error>> {
// Our 2x3 test array
let array = array![[1, 2, 3], [4, 5, 6]];
// Write the array into the file.
{
let file = File::create("test.csv")?;
let mut writer = WriterBuilder::new().has_headers(false).from_writer(file);
writer.serialize_array2(&array)?;
}
// Read an array back from the file
let file = File::open("test2.csv")?;
let mut reader = ReaderBuilder::new().has_headers(true).from_reader(file);
let array_read: Array2<u64> = reader.deserialize_array2((2, 3))?;
// Ensure that we got the original array back
assert_eq!(array_read, array);
println!("{:?}", array_read);
Ok(())
}
main();
[E0308] Error: mismatched types
╭─[command_37:1:1]
│
22 │ writer.serialize_array2(&array)?;
│ ────────┬─────── ───┬──
│ ╰──────────────── arguments to this method are incorrect
│ │
│ ╰──── expected `&ArrayBase<OwnedRepr<_>, Dim<...>>`, found `&ArrayBase<OwnedRepr<...>, ...>`
│
│ Note: note: method defined here
────╯
[E0308] Error: `?` operator has incompatible types
╭─[command_37:1:1]
│
28 │ let array_read: Array2<u64> = reader.deserialize_array2((2, 3))?;
│ ─────────────────┬────────────────
│ ╰────────────────── expected `ArrayBase<OwnedRepr<u64>, Dim<...>>`, found `ArrayBase<OwnedRepr<_>, Dim<...>>`
────╯
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Decision trees.
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
Machine learning: supervised vs. unsupervised
Supervised
- Labeled data
- Example 1: images labeled with the objects: cat, dog, monkey, elephant, etc.
- Example 2: medical data labeled with likelihood of cancer
- Goal: discover a relationship between attributes to predict unknown labels
Unsupervised
- Unlabeled data
- Want to discover a relationship between data points
- Examples:
- clustering: partition your data into groups of similar objects
- dimension reduction: for high dimensional data discover important attributes
Machine learning: Predictive vs descriptive vs prescriptive analytics
Descriptive
Use our data to explain what has happened in the past (i.e. find patterns in data that has already been observed)
Predictive
Use our data to predict what may happen in the future (i.e. apply the observed patterns to new observations and predict outcomes)
Prescriptive
Use our data and model to inform decisions we can make to achieve certain outcomes. This assumes a certain level of control over the data inputs to whatever process is being modeled. If no such control exists then prescriptive is not possible.
Supervised learning: Decision trees
Popular machine learning tool for predictive data analysis:
- rooted tree
- start at the root and keep going down
- every internal node labeled with a condition
- if satisfied, go left
- if not satisfied, go right
- leafs labeled with predicted labels
Does a player like bluegrass?

// First lets read in the sample data
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
:dep ndarray = { version = "^0.15.6" }
use ndarray::Array2;
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct SerRecord {
name: String,
number: usize,
year_born: usize,
total_points: usize,
PPG: f64,
}
let mut rdr = csv::Reader::from_path("players.csv").unwrap();
let mut v:Vec<SerRecord> = Vec::new();
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:SerRecord = result.expect("a CSV record");
v.push(record);
}
println!("{:#?}", v);
[
SerRecord {
name: "Kareem",
number: 33,
year_born: 1947,
total_points: 38387,
PPG: 24.6,
},
SerRecord {
name: "Karl",
number: 32,
year_born: 1963,
total_points: 36928,
PPG: 25.0,
},
SerRecord {
name: "LeBron",
number: 23,
year_born: 1984,
total_points: 36381,
PPG: 27.0,
},
SerRecord {
name: "Kobe",
number: 24,
year_born: 1978,
total_points: 33643,
PPG: 25.0,
},
SerRecord {
name: "Michael",
number: 23,
year_born: 1963,
total_points: 32292,
PPG: 30.1,
},
]
Heuristics for constructing decision trees -- I
- Start from a single node with all samples
- Iterate:
- select a node
- use the samples in the node to split it into children using some splitting criteria
- pass each sample to respective child
- Label leafs
Let's try to predict what a player's favorite color is?
![[Decision tree]](modules/media/dt-1.png)
Heuristics for constructing decision trees -- II
- Start from a single node with all samples
- Iterate:
- select a node
- use the samples in the node to split it into children using some splitting criteria
- pass each sample to respective child
- Label leafs
We'll split on PPG.
The goal is to have each leaf be a single class.
Favorite color?
![[Decision tree]](modules/media/dt-2.png)
Heuristics for constructing decision trees -- III
- Start from a single node with all samples
- Iterate:
- select a node
- use the samples in the node to split it into children using some splitting criteria
- pass each sample to respective child
- Label leafs
![[Decision tree]](modules/dt-3.png)
Heuristics for constructing decision trees -- IV
- Start from a single node with all samples
- Iterate:
- select a node
- use the samples in the node to split it into children
- pass each sample to respective child
- Label leafs
Favorite color?
![[Decision tree]](modules/media/dt-4.png)
Split selection
- Typical heuristic: select a split that improves classification most
- Various measures of "goodness" or "badness":
- Information gain / Entropy
- Ginni impurity
- Variance
Popular algorithms
- ID3
- C4.5
- C5.0
- CART (used by
linfa-trees,rustlearn, andscikit-learn)
You can read more about those algorithms at https://scikit-learn.org/stable/modules/tree.html#tree-algorithms-id3-c4-5-c5-0-and-cart
and see the mathematical formulation for CART here: https://scikit-learn.org/stable/modules/tree.html#mathematical-formulation
The Gini coefficient and Entropy (Impurity Measures)
-
Let's assume we have k classes that we are trying to decide.
-
We can estimate the probability by:
- A node M containing N samples has a Gini coefficient defined as follows:
- Or entropy defined by:
Advantages and disadvantages of decision trees
Advantages:
- easy to interpret
- not much data preparation needed
- categorical and numerical data
- relatively fast
Disadvantages:
- can be very sensitive to data changes
- can create an overcomplicated tree that matches the sample, but not the underlying problem
- hard to find an optimal tree
Decision tree construction using linfa-tree
https://rust-ml.github.io/linfa/, https://crates.io/crates/linfa
https://docs.rs/linfa-trees/latest/linfa_trees/
Note: ignore machine learning context for now
First, we read our sample data and add information who likes pizza
Visualized
// Rust 2021
//:dep plotters={version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"]}
// Rust 2024
:dep plotters={version = "^0.3.0", default-features = false, features = ["evcxr", "all_series"]}
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
:dep ndarray = { version = "^0.15.6" }
use ndarray::Array2;
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct SerRecord {
name: String,
number: usize,
year_born: usize,
total_points: usize,
PPG: f64,
}
let mut rdr = csv::Reader::from_path("players.csv").unwrap();
let mut v:Vec<SerRecord> = Vec::new();
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:SerRecord = result.expect("a CSV record");
v.push(record);
}
let mut flat_values: Vec<f64> = Vec::new();
for s in &v {
flat_values.push(s.total_points as f64);
flat_values.push(s.PPG);
flat_values.push(s.year_born as f64);
flat_values.push(s.number as f64);
}
let array = Array2::from_shape_vec((v.len(), 4), flat_values).expect("Error creating ndarray");
println!("{:?}", array);
let likes_pizza = [1,0,0,1,0];
extern crate plotters;
use plotters::prelude::*;
{
let x_values = array.column(0);
let y_values = array.column(1);
evcxr_figure((800, 800), |root| {
let mut chart = ChartBuilder::on(&root)
// the caption for the chart
.caption("Scatter Plot", ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
.build_cartesian_2d(32000f64..39000f64, 24f64..31f64)?;
// the X and Y coordinates spaces for the chart
chart.configure_mesh()
.x_desc("Total Points")
.y_desc("PPG")
.draw()?;
chart.draw_series(
x_values.iter()
.zip(y_values.iter())
.zip(likes_pizza.iter())
.map(|((total, ppg), likes)| {
let point = (*total, *ppg);
let size = 20;
let color = Palette99::pick(*likes as usize % 10); // Choose color based on 'LikesPizza'
Circle::new(point, size as i32, color.filled())
})
)?;
Ok(())
})}
The type of the variable v was redefined, so was lost.
[[38387.0, 24.6, 1947.0, 33.0],
[36928.0, 25.0, 1963.0, 32.0],
[36381.0, 27.0, 1984.0, 23.0],
[33643.0, 25.0, 1978.0, 24.0],
[32292.0, 30.1, 1963.0, 23.0]], shape=[5, 4], strides=[4, 1], layout=Cc (0x5), const ndim=2
Question:
If we were to try to split RED and GREEN based on PPG, where would we split?
Data selection
- set of inputs:
X - set of desired outputs:
y
Decision tree construction
- How to decide which feature should be located at the root node,
- Most accurate feature to serve as internal nodes or leaf nodes,
- How to divide tree,
- How to measure the accuracy of splitting tree and many more.
First the preamble with all the dependencies and the code to read the CSV file
//:dep plotters={version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"]}
:dep csv = { version = "^1.3" }
:dep serde = { version = "^1", features = ["derive"] }
:dep ndarray = { version = "^0.15.6" }
:dep linfa = { git = "https://github.com/rust-ml/linfa" }
:dep linfa-trees = { git = "https://github.com/rust-ml/linfa" }
use ndarray::Array2;
use ndarray::array;
use linfa_trees::DecisionTree;
use linfa::prelude::*;
// This lets us write `#[derive(Deserialize)]`.
use serde::Deserialize;
use std::fs::File;
use std::io::Write;
// We don't need to derive `Debug` (which doesn't require Serde), but it's a
// good habit to do it for all your types.
//
// Notice that the field names in this struct are NOT in the same order as
// the fields in the CSV data!
#[derive(Debug, Deserialize)]
#[serde(rename_all = "PascalCase")]
struct SerRecord {
name: String,
number: usize,
year_born: usize,
total_points: usize,
PPG: f64,
}
fn process_csv_file() -> Vec<SerRecord> {
let mut rdr = csv::Reader::from_path("players.csv").unwrap();
let mut v:Vec<SerRecord> = Vec::new();
// Loop over each record.
for result in rdr.deserialize() {
// An error may occur, so abort the program in an unfriendly way.
// We will make this more friendly later!
let record:SerRecord = result.expect("a CSV record");
v.push(record);
}
return v;
}
And the code to construct, train and measure a decision tree
We use the linfa Dataset:
- The most commonly used typed of dataset.
- It contains a number of records stored as an Array2 and
- each record may correspond to multiple targets.
- The targets are stored as an Array1 or Array2.
And construct a DecisionTree structure.
Then export to a TeX file and render the tree.
fn main() {
let mut v = process_csv_file();
let mut flat_values: Vec<f64> = Vec::new();
for s in &v {
flat_values.push(s.total_points as f64);
flat_values.push(s.PPG);
flat_values.push(s.year_born as f64);
}
let array = Array2::from_shape_vec((v.len(), 3), flat_values).expect("Error creating ndarray");
let likes_pizza = array![1,0,0,1,0];
let dataset = Dataset::new(array, likes_pizza).with_feature_names(vec!["total points", "PPG", "year born"]);
let decision_tree = DecisionTree::params()
.max_depth(Some(2))
.fit(&dataset)
.unwrap();
let accuracy = decision_tree.predict(&dataset).confusion_matrix(&dataset).unwrap().accuracy();
println!("The accuracy is: {:?}", accuracy);
let mut tikz = File::create("decision_tree_example.tex").unwrap();
tikz.write_all(
decision_tree
.export_to_tikz()
.with_legend()
.to_string()
.as_bytes(),
)
.unwrap();
println!(" => generate tree description with `latex decision_tree_example.tex`!");
}
main();
The type of the variable rdr was redefined, so was lost.
The type of the variable array was redefined, so was lost.
The accuracy is: 0.8
=> generate tree description with `latex decision_tree_example.tex`!
use std::process::Command;
let output = Command::new("pwd").output().expect("Failed to execute");
let output = Command::new("pdflatex").arg("decision_tree_example.tex").output().expect("Failed to execute");
let output = Command::new("sips").args(["-s", "format", "png", "decision_tree_example.pdf", "--out", "decision_tree_example.png"])
.output().expect("Failed to execute");

"Impurity" is another term for Gini index.
Note that Impurity decreases as we do more splits.
Also note that we can overfit the dataset. Will do worse on new data.
Techniques to avoid overfitting include setting a maximum tree depth.
Technical Coding Challenge
Coding Challenge
Coding Challenge Review
Linear Regression, Loss, and Bias
About This Module
Prework
Prework Reading
Pre-lecture Reflections
Lecture
Learning Objectives
Simplest setting
Input: set of points in
-
What function explains the relationship of 's with 's?
-
What linear function describes it best?
Multivariate version
Input: set of points in
Find linear function that describes 's in terms of 's?
Why linear regression?
- Have to assume something!
- Models hidden linear relationship + noise
Typical objective: minimize square error
-
Points rarely can be described exactly using a linear relationship
-
How to decide between several non-ideal options?
-
Typically want to find that minimizes total square error:
What about Categorical Data?
- Convert to numerical first
- One way is to simply convert to unique integers
- A better way is to create N new columns (one for each category) and make them boolean (is_x, is_y, is_z etc) -- one hot encoding
For example with 3 categories:
1-D Example
We'll start with an example from the Rust Machine Learning Book.
// Use a crate built from source on github
:dep linfa-book = { git = "https://github.com/rust-ml/book" }
:dep ndarray = { version = "^0.15.6" }
// create_curve implemented at https://github.com/rust-ml/book/blob/main/src/lib.rs#L52
use linfa_book::create_curve;
use ndarray::Array2;
use ndarray::s;
fn generate_data(output: bool) -> Array2<f64> {
/*
* Generate a dataset of x and y values
*
* - Randomly generate 50 points between 0 and 7
* - Calculate y = m * x^power + b +noise
* where noise is uniformly random between -0.5 and 0.5
*
* m = 1.0 (slope)
* power = 1.0 (straight line)
* b = 0.0 (y-intercept)
* num_points = 50
* x_range = [0.0, 7.0]
*
* This produces a 50x2 Array2<f64> with the first column being x and the
* second being y
*/
let array: Array2<f64> = linfa_book::create_curve(1.0, 1.0, 0.0, 50, [0.0, 7.0]);
// Converting from an array to a Linfa Dataset can be the trickiest part of this process
// The first part has to be an array of arrays even if they have a single entry for the 1-D case
// The underlying type is kind of ugly but thankfully the compiler figures it out for us
// let data: ArrayBase<OwnedRepr<f64>, Ix2> = .... is the actual type
// The second part has to be an array of values.
// let targets: Array1<f64> is the actual type
let data = array.slice(s![.., 0..1]).to_owned();
let targets = array.column(1).to_owned();
if output {
println!("The original array is:");
println!("{:.2?}", array);
println!("The data is:");
println!("{:.2?}", data);
println!("The targets are:");
println!("{:.2?}", targets);
}
return array;
}
generate_data(true);
The original array is:
[[6.59, 6.85],
[2.49, 2.39],
[0.77, 0.32],
[1.85, 2.25],
[2.13, 2.46],
[0.93, 0.60],
[6.17, 6.51],
[1.91, 2.02],
[2.82, 3.20],
[0.55, 0.23],
[4.31, 4.06],
[4.04, 3.54],
[6.15, 6.51],
[0.10, -0.33],
[0.68, 0.77],
[1.03, 1.18],
[0.51, 0.68],
[3.75, 3.38],
[1.59, 1.57],
[5.77, 6.26],
[1.18, 1.15],
[2.99, 2.99],
[4.33, 4.69],
[1.36, 1.52],
[5.20, 5.67],
[6.18, 6.41],
[6.10, 6.46],
[6.82, 6.68],
[4.27, 3.88],
[1.67, 1.71],
[5.42, 5.62],
[2.47, 2.02],
[4.48, 4.95],
[1.82, 2.27],
[5.53, 5.27],
[0.52, 0.53],
[5.63, 5.35],
[0.13, 0.43],
[4.47, 4.83],
[0.58, 1.00],
[3.13, 3.28],
[6.84, 6.69],
[6.46, 6.15],
[6.04, 6.27],
[5.63, 6.12],
[1.60, 1.86],
[0.18, 0.08],
[6.24, 6.70],
[0.20, 0.06],
[4.44, 4.10]], shape=[50, 2], strides=[2, 1], layout=Cc (0x5), const ndim=2
The data is:
[[6.59],
[2.49],
[0.77],
[1.85],
[2.13],
[0.93],
[6.17],
[1.91],
[2.82],
[0.55],
[4.31],
[4.04],
[6.15],
[0.10],
[0.68],
[1.03],
[0.51],
[3.75],
[1.59],
[5.77],
[1.18],
[2.99],
[4.33],
[1.36],
[5.20],
[6.18],
[6.10],
[6.82],
[4.27],
[1.67],
[5.42],
[2.47],
[4.48],
[1.82],
[5.53],
[0.52],
[5.63],
[0.13],
[4.47],
[0.58],
[3.13],
[6.84],
[6.46],
[6.04],
[5.63],
[1.60],
[0.18],
[6.24],
[0.20],
[4.44]], shape=[50, 1], strides=[1, 1], layout=CFcf (0xf), const ndim=2
The targets are:
[6.85, 2.39, 0.32, 2.25, 2.46, 0.60, 6.51, 2.02, 3.20, 0.23, 4.06, 3.54, 6.51, -0.33, 0.77, 1.18, 0.68, 3.38, 1.57, 6.26, 1.15, 2.99, 4.69, 1.52, 5.67, 6.41, 6.46, 6.68, 3.88, 1.71, 5.62, 2.02, 4.95, 2.27, 5.27, 0.53, 5.35, 0.43, 4.83, 1.00, 3.28, 6.69, 6.15, 6.27, 6.12, 1.86, 0.08, 6.70, 0.06, 4.10], shape=[50], strides=[1], layout=CFcf (0xf), const ndim=1
Let's plot these points to see what they look like
// 2021
//:dep plotters={version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"]}
// 2024
:dep plotters={version = "^0.3.0", default-features = false, features = ["evcxr", "all_series"]}
:dep ndarray = { version = "^0.15.6" }
extern crate plotters;
use plotters::prelude::*;
{
let array: Array2<f64> = generate_data(false);
let x_values = array.column(0);
let y_values = array.column(1);
evcxr_figure((640, 480), |root| {
let mut chart = ChartBuilder::on(&root)
// the caption for the chart
.caption("2-D Plot", ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
// the X and Y coordinates spaces for the chart
.build_cartesian_2d(0f64..8f64, 0f64..8f64)?;
chart.configure_mesh()
.x_desc("X Values")
.y_desc("Y Values")
.draw()?;
chart.draw_series(
x_values.iter().zip(y_values.iter()).map(|(&x, &y)| {
Circle::new((x, y), 3, RED.filled())
}),
)?;
Ok(())
})
}
Let's fit a linear regression to it
// There are multiple packages in this git repository so we have to declare
// all the ones we care about
:dep linfa = { git = "https://github.com/rust-ml/linfa" }
:dep linfa-linear = { git = "https://github.com/rust-ml/linfa" }
:dep ndarray = { version = "^0.15.6" }
// Now we need to declare which function we are going to use
use linfa::Dataset;
use linfa_linear::LinearRegression;
use linfa_linear::FittedLinearRegression;
use linfa::prelude::*;
fn fit_model(array: &Array2<f64>) -> FittedLinearRegression<f64> {
// Let's regenarate and split our data
let data = array.slice(s![.., 0..1]).to_owned();
let targets = array.column(1).to_owned();
// And finally let's fit a linear regression to it
println!("Data: {:?} \n Targets: {:?}", data, targets);
let dataset = Dataset::new(data, targets);
let lin_reg: LinearRegression = LinearRegression::new();
let model: FittedLinearRegression<f64> = lin_reg.fit(&dataset).unwrap();
let ypred = model.predict(&dataset);
let loss = (dataset.targets() - ypred)
.mapv(|x| x.abs())
.mean();
println!("{:?}", loss);
return model;
}
let array: Array2<f64> = generate_data(false);
let model = fit_model(&array);
println!("{:?}", model);
Data: [[6.381616680690672],
[4.396361662331629],
[4.3324365575773305],
[0.8289740051702756],
[6.319103537997485],
[0.3335321841860137],
[5.095836624614474],
[3.6492182454480435],
[1.3364352957815282],
[0.09639507860613405],
[5.303183512825285],
[4.2951694397460285],
[5.4057438081138915],
[0.10960286365816452],
[4.603044369250634],
[4.024864366257263],
[4.281935499419392],
[4.06157301198745],
[5.755333890324657],
[1.3359866701598488],
[2.3904258537567324],
[4.029842664366427],
[2.2848232403062685],
[0.12639520987084052],
[2.9318196797275835],
[3.4846905959349144],
[2.1132653187529598],
[2.409170009823532],
[1.294104964714346],
[3.068189601192284],
[1.5698399649061598],
[4.585070111032277],
[0.9080582927284744],
[2.3500918290692145],
[5.412834219057823],
[0.5732492542928671],
[3.1955234173749907],
[0.6011335403952247],
[0.06756207483950094],
[0.4973826225929374],
[3.5708462015304976],
[5.016449358044835],
[6.275456045849482],
[0.24134187530345663],
[0.19382724586379352],
[3.900026524938423],
[1.977100227563272],
[4.934898600624889],
[3.970926362145382],
[1.5789373737594155]], shape=[50, 1], strides=[1, 1], layout=CFcf (0xf), const ndim=2
Targets: [6.74548949826222, 4.178753589022698, 3.9296433463393803, 0.9101170752817256, 6.422143609882557, -0.115321608937899, 5.126622670184417, 4.001921017212379, 1.2316076794171344, 0.3251034025687174, 5.291327977564027, 4.740353143641885, 5.005473769290836, -0.3802551719385241, 4.723355959069144, 3.740167334494597, 3.869317273792087, 3.583182714685261, 5.960145733182379, 1.4154622808579058, 2.395483563478454, 3.780181818550531, 2.195179330427658, -0.0780379205920585, 3.3559033104968132, 3.595446926448168, 1.9151631312465982, 2.5817866309609263, 1.1115468223706244, 3.2978733650316716, 1.7303235376317656, 4.577920815363182, 0.7328128405941892, 1.8555370714021548, 5.259719826144993, 0.46486256898256517, 3.661623687684834, 0.24442021204114717, 0.26510910851412994, 0.8471086226984335, 3.373961998065203, 4.696005829425596, 5.854185825360939, 0.3863210554131675, 0.29817841644956, 3.7047013726196827, 2.027075695584828, 5.171080561424032, 3.949876872423843, 2.0560366719493564], shape=[50], strides=[1], layout=CFcf (0xf), const ndim=1
Some(0.23628401752752)
FittedLinearRegression { intercept: -0.016055504752757018, params: [0.9953569138666288], shape=[1], strides=[1], layout=CFcf (0xf), const ndim=1 }
Finally let's put everything together and plot the data points and model line
extern crate plotters;
use plotters::prelude::*;
{
let array: Array2<f64> = generate_data(false);
let model = fit_model(&array);
println!("{:?}", model);
let x_values = array.column(0);
let y_values = array.column(1);
evcxr_figure((640, 480), |root| {
let mut chart = ChartBuilder::on(&root)
// the caption for the chart
.caption("Linear Regression", ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
// the X and Y coordinates spaces for the chart
.build_cartesian_2d(0f64..8f64, 0f64..8f64)?;
chart.configure_mesh()
.x_desc("X Values")
.y_desc("Y Values")
.draw()?;
chart.draw_series(
x_values.iter().zip(y_values.iter()).map(|(&x, &y)| {
Circle::new((x, y), 3, RED.filled())
}),
)?;
let mut line_points = Vec::with_capacity(2);
for i in (0..8i32).step_by(1) {
line_points.push((i as f64, (i as f64 * model.params()[0]) + model.intercept()));
}
// We can configure the rounded precision of our result here
let precision = 2;
let label = format!(
"y = {:.2$}x + {:.2}",
model.params()[0],
model.intercept(),
precision
);
chart.draw_series(LineSeries::new(line_points, &BLACK))
.unwrap()
.label(&label);
Ok(())
})
}
Data: [[2.04750415763924],
[6.367873757109327],
[6.398058085002853],
[2.768792455803591],
[0.1718068124456904],
[5.410322501484772],
[1.16759081573306],
[2.7536979999018953],
[4.950802437871839],
[0.6025334876065953],
[3.2764831065673183],
[1.721556072918826],
[2.944603890742717],
[1.1679420030984646],
[1.4583480833464897],
[5.603000967206449],
[0.7792958771030705],
[0.9903895595193106],
[5.849216682555504],
[5.039598826115972],
[6.79519856325383],
[5.9811481574554595],
[5.848135244005015],
[3.2303889196020474],
[5.180333900515606],
[6.441584502170909],
[2.1595411034915752],
[0.7565248539761933],
[6.575497606063534],
[4.5995576454693055],
[4.3608367164107875],
[5.548520783489524],
[6.525459030458023],
[0.6937753120972134],
[1.9522048348466015],
[2.2341967770269227],
[3.637038438411855],
[2.2190157648753184],
[2.681992233899634],
[5.566572415187922],
[0.9357604528754049],
[0.8490168837359822],
[6.448593818753438],
[2.6758983352983177],
[1.049091617939221],
[1.5851990026054852],
[6.098462409705635],
[2.585742190451155],
[0.17671676593123875],
[0.5246679878163918]], shape=[50, 1], strides=[1, 1], layout=CFcf (0xf), const ndim=2
Targets: [2.408804027014255, 6.469323578131448, 6.193104604093066, 2.418915373474102, 0.029226368788591195, 4.9972110392473255, 1.1150716816343442, 2.926060993136029, 4.490694341852246, 0.9502150297756105, 3.4740768014974783, 1.251263397177235, 3.4148633041576995, 1.4681943013079881, 0.9890758429931192, 5.391821032945574, 1.211034580394566, 1.3854290271879017, 5.431409730804429, 4.699669709042999, 6.998217208006695, 6.109111375789134, 5.75094664694154, 3.658429812887407, 5.289801849698538, 6.105335877939171, 1.8358314904060669, 0.36311224569624856, 6.342541141255715, 4.691208846854487, 4.250255794021059, 5.675447984854635, 6.793126113768862, 0.5931705314387281, 2.111835341368409, 2.144381384764876, 3.8510929693234646, 1.7549171320182217, 2.563236265429576, 5.214375657851614, 0.8020824408564826, 0.7138795774936122, 6.183001994443131, 2.633962608410515, 1.4663428201689852, 1.6261732010691712, 6.5133103394465035, 2.1115834556736774, 0.5083760324119229, 0.7979776364877389], shape=[50], strides=[1], layout=CFcf (0xf), const ndim=1
Some(0.25864023660929314)
FittedLinearRegression { intercept: 0.05790152043058407, params: [0.9754302443444729], shape=[1], strides=[1], layout=CFcf (0xf), const ndim=1 }
paramsinterceptin
Coefficient of determination (or )
-
How good is my function ?
-
Input: points
-
Idea: Compare variance of 's to the deviation of 's from 's
-
Formally:
where
- Range: (should be in for linear regression)
Let's compute for our data
:dep linfa = { git = "https://github.com/rust-ml/linfa" }
:dep linfa-linear = { git = "https://github.com/rust-ml/linfa" }
:dep ndarray = { version = "^0.15.6" }
:dep ndarray-stats = { version = "^0.5.1" }
let array: Array2<f64> = generate_data(false);
let data = array.slice(s![.., 0..1]).to_owned();
let targets = array.column(1).to_owned();
// And finally let's fit a linear regression to it
let dataset = Dataset::new(data, targets).with_feature_names(vec!["x"]);
let lin_reg: LinearRegression = LinearRegression::new();
let model: FittedLinearRegression<f64> = lin_reg.fit(&dataset).unwrap();
let ypred = model.predict(&dataset);
//
let variance:f64 = dataset.targets().var(0.0);
let mse:f64 = (dataset.targets() - ypred)
.mapv(|x| x.powi(2))
.mean().unwrap();
let r2 = 1.0 - mse/variance;
println!("variance = {:.3}, mse = {:.3}, R2 = {:.3}", variance, mse, r2);
variance = 2.971, mse = 0.080, R2 = 0.973
Multivariable linear regression
What if you have multiple input variables and one output variable?
It's actually quite simple. The same code we used above but make sure your X side contains multiple values for each of the variables in your function. The code will compute as many coefficients as the variables it sees.
For 3-D input:
:dep linfa = { git = "https://github.com/rust-ml/linfa" }
:dep linfa-linear = { git = "https://github.com/rust-ml/linfa" }
:dep ndarray = { version = "^0.15.6" }
use linfa::Dataset;
use linfa::traits::Fit;
use ndarray::{Array1, Array2, array};
use linfa_linear::LinearRegression;
use linfa_linear::FittedLinearRegression;
use linfa::prelude::*;
fn main() {
// Example data: 4 samples with 3 features each
let x: Array2<f64> = array![[1.0, 2.0, 3.0],
//[2.0, 3.0, 1.0],
[2.0, 3.0, 4.0],
[3.0, 4.0, 5.0],
[4.0, 5.0, 6.0],
//[6.0, 11.0, 12.0]
];
// Target values
let y: Array1<f64> = array![6.0,
//6.0,
9.0,
12.0,
15.0,
//29.0,
];
// Create dataset
let dataset = Dataset::new(x.clone(), y.clone());
// Fit linear regression model
let lin_reg = LinearRegression::new();
let model = lin_reg.fit(&dataset).unwrap();
// Print coefficients
println!("Coefficients: {:.3?}", model.params());
println!("Intercept: {:.3?}", model.intercept());
// Predict using the fitted model
let predictions = model.predict(&x);
println!("Predictions: {:.3?}", predictions);
}
main();
Coefficients: [22.667, -8.333, -11.333], shape=[3], strides=[1], layout=CFcf (0xf), const ndim=1
Intercept: 34.000
Predictions: [6.000, 9.000, 12.000, 15.000], shape=[4], strides=[1], layout=CFcf (0xf), const ndim=1
General Least Squares Fit
We can generalize the ordinary least squares regression problem, by trying, for example, to find the in an equation like
to minize the differences between some targets and the .
Note that these are still linear in the parameters.
We can rewrite this in matrix form:
where the matrix of 's is sometimes called the Design Matrix.
-
We are going to use a different library familar to us from the ndarray lecture.
-
ndarray-linalg can compute the parameters to fit an arbitrary function as long as you have some idea of what the function might be.
- e.g. express it as a design matrix
-
Then solve a system of linear equations with that matrix as the left hand side and our observed values as the right hand side.
-
The result is the missing parameters of our assumed function
:dep ndarray = { version = "^0.15.6" }
// See ./README.md for ndarray-linalg prereqs
// This is the version for MAC
:dep ndarray-linalg = { version = "^0.16", features = ["openblas-system"] }
// Alternative for Mac if you installed netlib
//:dep ndarray-linalg = { version = "^0.14" , features = ["netlib"]}
// This works for linux
// :dep ndarray-linalg = { version = "^0.14" , features = ["openblas"]}
use ndarray::{Array1, Array2, ArrayView1};
use ndarray_linalg::Solve;
use ndarray::array;
use ndarray::Axis;
use ndarray_linalg::LeastSquaresSvd;
// Define an arbitrary function (e.g., a quadratic function)
fn arbitrary_function(x: f64, params: &ArrayView1<f64>) -> f64 {
params[0] + params[1] * x + params[2] * x * x
}
// Compute the design matrix for the arbitrary function
fn design_matrix(x: &Array1<f64>) -> Array2<f64> {
let mut dm = Array2::<f64>::zeros((x.len(), 3));
for (i, &xi) in x.iter().enumerate() {
dm[(i, 0)] = 1.0;
dm[(i, 1)] = xi;
dm[(i, 2)] = xi * xi;
}
dm
}
// Perform least squares fit
fn least_squares_fit(x: &Array1<f64>, y: &Array1<f64>) -> Array1<f64> {
let dm = design_matrix(x);
let y_col = y.to_owned().insert_axis(Axis(1)); // Convert y to a column vector
let params = dm.least_squares(&y_col).unwrap().solution; // Use least squares solver
params.column(0).to_owned() // Convert params back to 1D array
}
fn main() {
// Example data
let x: Array1<f64> = array![1.0, 2.0, 3.0, 4.0];
let y: Array1<f64> = array![1.0, 4.0, 9.0, 16.0]; // y = x^2 for this example
// Perform least squares fit
let params = least_squares_fit(&x, &y);
println!("Fitted parameters: {:.3}", params);
// Predict using the fitted parameters
let predictions: Array1<f64> = x.mapv(|xi| arbitrary_function(xi, ¶ms.view()));
println!("Predictions: {:.3?}", predictions);
}
main();
The type of the variable dataset was redefined, so was lost.
The type of the variable array was redefined, so was lost.
The type of the variable model was redefined, so was lost.
The type of the variable lin_reg was redefined, so was lost.
Fitted parameters: [0.000, -0.000, 1.000]
Predictions: [1.000, 4.000, 9.000, 16.000], shape=[4], strides=[1], layout=CFcf (0xf), const ndim=1
Example General Function
Imagine a case where you have a function like :
Then setup your functions like this:
// Define an arbitrary function (e.g., a quadratic function)
fn arbitrary_function(x: f64, params: &ArrayView1<f64>) -> f64 {
params[0] + params[1] * x + params[2] * x * x + params[3] * x.ln()
}
// Compute the design matrix for the arbitrary function
fn design_matrix(x: &Array1<f64>) -> Array2<f64> {
let mut dm = Array2::<f64>::zeros((x.len(), 4));
for (i, &xi) in x.iter().enumerate() {
dm[(i, 0)] = 1.0;
dm[(i, 1)] = xi;
dm[(i, 2)] = xi * xi;
dm[(i, 3)] = xi.ln();
}
dm
}
It gets messier if x appears in exponents and outside the scope of this lecture but it is possible to do non-linear least squares fit for completely arbitrary functions!!!
Train/Test Splits
To test the generality of your models, it is recommended to split your data into
- training dataset (e.g. 80% of the data)
- testing dataset (e.g. 20% of the data)
Then train with the training dataset and evaluate using the test dataset.
It is a bit more cumbersome in Rust than in scikit-learn in python but in the end not that hard
The smartcore crate implements this function for you and you can use it as follows
:dep linfa = { git = "https://github.com/rust-ml/linfa" }
:dep linfa-linear = { git = "https://github.com/rust-ml/linfa" }
:dep ndarray = {version = "0.15"}
:dep smartcore = {version = "0.2", features=["ndarray-bindings"]}
use linfa::Dataset;
use linfa::traits::Fit;
use linfa_linear::LinearRegression;
use ndarray::{Array1, Array2, array};
use linfa::DatasetBase;
use smartcore::model_selection::train_test_split; // This is the function we need
use smartcore::linalg::naive::dense_matrix::DenseMatrix;
use smartcore::linalg::BaseMatrix;
fn main() {
// Example data: 4 samples with 3 features each
let x: Array2<f64> = array![[1.0, 2.0, 3.0],
[2.0, 3.0, 4.0],
[3.0, 4.0, 5.0],
[4.0, 5.0, 6.0]];
// Target values
let y: Array1<f64> = array![6.0, 9.0, 12.0, 15.0];
// Split the data into training and testing sets
let (x_train, x_test, y_train, y_test) = train_test_split(&x, &y, 0.5, true);
let train_dataset = Dataset::new(x_train.clone(), y_train.clone());
let test_dataset = Dataset::new(x_test.clone(), y_test.clone());
// Fit linear regression model to the training data
let lin_reg = LinearRegression::new();
let model = lin_reg.fit(&train_dataset).unwrap();
// Print coefficients
println!("Coefficients: {:.3?}", model.params());
println!("Intercept: {:.3?}", model.intercept());
// Predict from the test set
let predictions = model.predict(&x_test);
println!("X_test: {:.3?}, Predictions: {:.3?}", x_test, predictions);
}
main();
Coefficients: [1.000, 1.000, 1.000], shape=[3], strides=[1], layout=CFcf (0xf), const ndim=1
Intercept: -0.000
X_test: [[4.000, 5.000, 6.000],
[3.000, 4.000, 5.000]], shape=[2, 3], strides=[3, 1], layout=Cc (0x5), const ndim=2, Predictions: [15.000, 12.000], shape=[2], strides=[1], layout=CFcf (0xf), const ndim=1
Loss Functions, Bias & Cross-Validation
Reminders
Typical predictive data analysis pipeline:
- Very important: split your data into a training and test part
- Train your model on the training part
- Use the testing part to evaluate accuracy
Measuring errors for regression
- Usually, the predictor is not perfect.
- How do I evaluate different options and choose the best one?
Mean Squared Error (or loss):
Mean Absolute Error (or loss):
Plots of MSE and MAE
// 2021
//:dep plotters={version = "^0.3.0", default_features = false, features = ["evcxr", "all_series","full_palette"]}
// 2024
:dep plotters={version = "^0.3.0", default-features = false, features = ["evcxr", "all_series","full_palette"]}
:dep ndarray = { version = "^0.16.0" }
:dep ndarray-rand = { version = "0.15.0" }
:dep linfa = { version = "^0.7.0" }
:dep linfa-linear = { version = "^0.7.0" }
:dep linfa-datasets = { version = "^0.7.0" }
:dep linfa-linear = { version = "^0.7.0" }
:dep ndarray-stats = { version = "^0.5.1" }
[E0277] Error: the trait bound `ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>: Matrix<_>` is not satisfied
[E0277] Error: the trait bound `ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>: BaseMatrix<_>` is not satisfied
[E0308] Error: mismatched types
[E0308] Error: mismatched types
[E0277] Error: the trait bound `FittedLinearRegression<_>: linfa::prelude::Predict<&ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>, _>` is not satisfied
[E0277] Error: the trait bound `ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>: Records` is not satisfied
[E0599] Error: no method named `least_squares` found for struct `ArrayBase` in the current scope
[E0308] Error: arguments to this function are incorrect
[E0308] Error: mismatched types
// Helper code for plotting
extern crate plotters;
use plotters::prelude::*;
use ndarray::Array1;
use plotters::evcxr::SVGWrapper;
use plotters::style::colors::full_palette;
fn plotter_scatter(sizes: (u32, u32), x_range: (f64, f64), y_range: (f64, f64), scatters: &[(&Array1<f64>, &Array1<f64>, &RGBColor, &str, &str)], lines: &[(&Array1<f64>, &Array1<f64>, &str, &RGBColor)]) -> SVGWrapper {
evcxr_figure((sizes.0, sizes.1), |root| {
let mut chart = ChartBuilder::on(&root)
// the caption for the chart
.caption("2-D Plot", ("Arial", 20).into_font())
.x_label_area_size(40)
.y_label_area_size(40)
// the X and Y coordinates spaces for the chart
.build_cartesian_2d(x_range.0..x_range.1, y_range.0..y_range.1)?;
chart.configure_mesh()
.x_desc("X Values")
.y_desc("Y Values")
.draw()?;
for scatter in scatters {
if scatter.3 == "x" {
chart.draw_series(
scatter.0.iter().zip(scatter.1.iter()).map(|(&a, &b)| {
Cross::new((a, b), 3, scatter.2.filled())
}),
)?
.label(scatter.4)
.legend(|(x, y)| Cross::new((x, y), 3, scatter.2.filled()));
} else {
chart.draw_series(
scatter.0.iter().zip(scatter.1.iter()).map(|(&a, &b)| {
Circle::new((a, b), 3, scatter.2.filled())
}),
)?
.label(scatter.4)
.legend(|(x, y)| Circle::new((x, y), 3, scatter.2.filled()));
}
}
if lines.len() > 0 {
for line in lines {
chart
.draw_series(LineSeries::new(line.0.iter().cloned().zip(line.1.iter().cloned()), line.3))?
.label(line.2)
.legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y )], line.3));
}
// Configure and draw the legend
}
chart
.configure_series_labels()
.background_style(&WHITE.mix(0.8))
.border_style(&BLACK)
.draw()?;
Ok(())
})
}
use ndarray::Array;
let xs = Array::linspace(-1.3, 1.3, 300);
let abs_xs = xs.mapv(f64::abs);
let xs_squared = xs.mapv(|a| a.powi(2));
plotter_scatter(
(500, 400), (-1.5,1.5), (0.,1.75), //plot size and ranges
&[], //any scatters
&[(&xs,&abs_xs, "MAE", &full_palette::RED), (&xs,&xs_squared, "MSE", &full_palette::BLUE)] //any lines
)
Observe that MAE will be more sensitive to small differences, while
MSE penalized big differences more.
Definition of an outlier
Important difference between error measures: different attention to outliers
Linear Regression: higher powers of absolute error ( loss)
In the limit...
-
This converges to minimizing the maximum difference between ( and )
-
This is called: loss
-
Another way to express it: minimize such that
In the limit...
- Another way to express it: minimize such that
- Linear programming formulation: minimize such that
and
1D insight into the outlier sensitivity
-
Input: set of points in
-
What point minimizes MSE, MAE, ... as a representative of these points?
-
MSE aka : mean
-
MAE aka : median
-
: the mean of the maximum and minimum
Something in between MSE and MAE?
-
loss for ?
-
Huber loss:
- quadratic for small distances
- linear for large distances

Underfitting
- Model not expressive enough to capture the problem
- Or a solution found does not match the problem
Possible solutions:
- Try harder to find a better solution
- Add more parameters
- Try a different model that captures the solution
Overfitting
- Predictions adjusted too well to training data
- Error on test data error on training data
Possible solutions:
- Don't optimize the model on the training data too much
- Remove features that are too noisy
- Add more training data
- Reduce model complexity
Bias and variance
Bias:
The simplifying assumptions made by the model to make the target function easier to approximate.
Mathematically it is the difference of the average value of predictions from the true function:
Variance:
The amount that the output of the model changes given different training data.
Mathematically it is the mean of the delta of the squared deviation of the prediction function from its expected value:
Bias: error due to model unable to match the complexity of the problem
Variance: how much the prediction will vary in response to data points
Overfitting: high variance, low bias
Underfitting: high bias, low variance
Important in practice:
-
detecting the source of problems: variance vs. bias, overfitting vs. underfitting
-
navigating the trade-off and finding the sweet spot
Some examples
| Algorithm | Bias| Variance| |:-:|:-:|:-:| |Linear Regression|High|Low| |Decision Tree|Low|High| |Random Forest|Low|High (less than tree)|
Terminology
Parameters
- Variables fixed in a specific instantiation of a model
- Examples:
- coefficients in linear regression
- decision tree structure and thresholds
- weights and thresholds in a neural network
Hyperparameters
-
Also parameters, but higher level
-
Examples:
- number of leafs in a decision tree
- number of layers and their structure in a neural network
- degree of a polynomial
Hyperparameter tuning
- Adjusting hyperparameters before training the final model
Model selection
- Deciding on the type of model to be used (linear regression? decision trees? ...)
Decision Tree discussion
- Tree structure and thresholds for splits are parameters (learned by the algorithm)
- Many of the others are hyperparameters
- split_quality: Sets the metric used to decide the feature on which to split a node
- min_impurity_decrease: How much reduction in gini or other metric should we see before we allow a split
- min_weight_split: Sets the minimum weight of samples required to split a node.
- min_weight_leaf: Sets the minimum weight of samples that a split has to place in each leaf
- max_depth: Affects the structure of the tree and how elements can be assigned to nodes
All documented at great length in (https://docs.rs/linfa-trees/latest/linfa_trees/struct.DecisionTreeParams.html)
Challenges of training and cross-validation
Big goal: train a model that can be used for predicting
Intermediate goal: select the right model and hyperparameters
Information leak danger!
- If we do it adaptively, information from the test set could affect the model selection
Tune your parameters by using portions of the training set and preserve the test set for only a final evaluation

Holdout method
-
Partition the training data again: training set and validation set
-
Use the validation part to estimate accuracy whenever needed
Pros:
- Very efficient
- Fine with lots of data when losing a fraction is not a problem
Cons:
- Yet another part of data not used for training
- Problematic when the data set is small
- Testing part could contain important information
–fold cross–validation
- Partition the training set into folds at random
- Repeat times:
- train on folds
- estimate the accuracy on the -th fold
- Return the mean
Pros:
- Every data point used for training most of the time
- Less variance in the estimate
Cons:
- times slower
LOOCV: Leave–one–out cross–validation
-
Extreme case of the previous approach: separate fold for each data point
-
For each data point :
- train on data without
- estimate the accuracy on
-
Return the mean of accuracies
Cons:
- Even more expensive
Many other options
-
Generalization: leave––out cross–validation enumerates over subsets
-
Sampling instead of trying all options
-
A variation that ensures that all classes evenly distributed in folds
-
...
Training and Cross Validation with Iris Dataset
Classic dataset
- 3 Iris species
- 50 examples in each class
- 4 features (sepal length/width, petal length/width) for each sample
:dep linfa = {version = "0.7.0"}
:dep linfa-datasets = { version = "0.7.0", features = ["iris"] }
:dep linfa-trees = { version = "0.7.0" }
:dep ndarray = { version = "0.16.1" }
:dep ndarray-rand = {version = "0.15.0" }
:dep rand = { version = "0.8.5", features = ["small_rng"] }
:dep smartcore = { version = "0.3.2", features = ["datasets", "ndarray-bindings"] }
use linfa::prelude::*;
use linfa_trees::DecisionTree;
use ndarray_rand::rand::SeedableRng;
use rand::rngs::SmallRng;
use linfa_trees::DecisionTreeParams;
fn crossvalidate() -> Result<(), Box<dyn std::error::Error>> {
// Load the Iris dataset
let mut iris = linfa_datasets::iris();
let mut rng = SmallRng::seed_from_u64(42);
// Split the data into training and testing sets
let (train, test) = iris.clone()
.shuffle(&mut rng)
.split_with_ratio(0.8);
// Extract the features (X) and target (y) for training and testing sets
let X_train = train.records();
let y_train = train.targets();
let X_test = test.records();
let y_test = test.targets();
// Print the shape of the training and testing sets
println!("X_train shape: ({}, {})", X_train.nrows(), X_train.ncols());
println!("y_train shape: ({})", y_train.len());
println!("X_test shape: ({}, {})", X_test.nrows(), X_test.ncols());
println!("y_test shape: ({})", y_test.len());
// Train the model on the training data
let model = DecisionTree::params()
.max_depth(Some(3))
.fit(&train)?;
// Evaluate the model's accuracy on the training set
let train_accuracy = model.predict(&train)
.confusion_matrix(&train)?
.accuracy();
println!("Training accuracy: {:.2}%", train_accuracy * 100.0);
// Evaluate the model's accuracy on the test set
let test_accuracy = model.predict(&test)
.confusion_matrix(&test)?
.accuracy();
println!("Test accuracy: {:.2}%", test_accuracy * 100.0);
// Define two models with depths 3 and 2
let dt_params1 = DecisionTree::params().max_depth(Some(3));
let dt_params2 = DecisionTree::params().max_depth(Some(2));
// Create a vector of models
let models = vec![dt_params1, dt_params2];
// Train and cross-validation using the models
let scores = iris.cross_validate_single(
5,
&models,
|prediction, truth|
Ok(prediction.confusion_matrix(truth.to_owned())?.accuracy()))?;
println!("Cross-validation scores: {:?}", scores);
// Perform cross-validation using fold
let scores: Vec<_> = iris.fold(5).into_iter().map(|(train, valid)| {
let model = DecisionTree::params()
.max_depth(Some(3))
.fit(&train).unwrap();
let accuracy = model.predict(&valid).confusion_matrix(&valid).unwrap().accuracy();
accuracy
}).collect();
println!("Cross-validation scores general: {:?} {}", scores, scores.iter().sum::<f32>()/scores.len() as f32);
Ok(())
}
crossvalidate();
[E0433] Error: failed to resolve: could not find `naive` in `linalg`
[E0432] Error: unresolved import `smartcore::linalg::BaseMatrix`
[E0277] Error: the trait bound `ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>: Array2<_>` is not satisfied
[E0277] Error: the trait bound `ArrayBase<OwnedRepr<f64>, Dim<[usize; 1]>>: Array1<_>` is not satisfied
[E0061] Error: this function takes 5 arguments but 4 arguments were supplied
[E0308] Error: arguments to this function are incorrect
[E0308] Error: arguments to this function are incorrect
[E0599] Error: the method `fit` exists for struct `LinearRegression`, but its trait bounds were not satisfied
[E0599] Error: no method named `least_squares` found for struct `ArrayBase` in the current scope
[E0308] Error: arguments to this function are incorrect
[E0599] Error: the method `fit` exists for struct `LinearRegression`, but its trait bounds were not satisfied
[E0308] Error: mismatched types
Let's take a closer look at
#![allow(unused)] fn main() { // Evaluate the model's accuracy on the training set let train_accuracy = model.predict(&train) .confusion_matrix(&train)? .accuracy(); println!("Training accuracy: {:.2}%", train_accuracy * 100.0); }
We're creating the confusion matrix, for example
Predicted
Class1 Class2 Class3
Actual Class1 TP1 FP12 FP13
Class2 FP21 TP2 FP23
Class3 FP31 FP32 TP3
Where:
- TP1, TP2, TP3 are True Positives for each class (correct predictions)
- FPxy are False Positives (predicting class y when it's actually class x)
And then calculating accuracy as:
Accuracy = (TP1 + TP2 + TP3) / Total Predictions
For the second training experiment:
#![allow(unused)] fn main() { // Define two models with depths 3 and 2 let dt_params1 = DecisionTree::params().max_depth(Some(3)); let dt_params2 = DecisionTree::params().max_depth(Some(2)); // Create a vector of models let models = vec![dt_params1, dt_params2]; // Train and cross-validation using the models let scores = iris.cross_validate_single(5, &models, |prediction, truth| Ok(prediction.confusion_matrix(truth.to_owned())?.accuracy()))?; println!("Cross-validation scores: {:?}", scores); }
dt_params1 and dt_params2 are just parameter configurations, not yet trained models.
We'll split the training set into 5 folds:
Initial Split: [Fold1, Fold2, Fold3, Fold4, Fold5]
Then train on 4 of the folds and validate on the 5th:
For Model 1 (max_depth=3):
Iteration 1: Train on [Fold2, Fold3, Fold4, Fold5], Validate on Fold1
Iteration 2: Train on [Fold1, Fold3, Fold4, Fold5], Validate on Fold2
Iteration 3: Train on [Fold1, Fold2, Fold4, Fold5], Validate on Fold3
Iteration 4: Train on [Fold1, Fold2, Fold3, Fold5], Validate on Fold4
Iteration 5: Train on [Fold1, Fold2, Fold3, Fold4], Validate on Fold5
For Model 2 (max_depth=2): Same process repeated with the same folds
And the last training experiment:
#![allow(unused)] fn main() { // Perform cross-validation using fold let scores: Vec<_> = iris.fold(5).into_iter().map(|(train, valid)| { let model = DecisionTree::params() .max_depth(Some(3)) .fit(&train).unwrap(); let accuracy = model.predict(&valid).confusion_matrix(&valid).unwrap().accuracy(); accuracy }).collect(); }
This manually implements 5-fold cross-validation.
Step-by-step description courtesy of Cursor Agent.
- Creating the Folds:
#![allow(unused)] fn main() { iris.fold(5) }
- This splits the Iris dataset into 5 folds
- Returns an iterator over tuples of
(train, valid)where:traincontains 4/5 of the datavalidcontains 1/5 of the data
- Each iteration will use a different fold as the validation set
- The Main Loop:
#![allow(unused)] fn main() { .into_iter().map(|(train, valid)| { }
- Converts the folds into an iterator
- For each iteration, we get a training set and validation set
- Model Training:
#![allow(unused)] fn main() { let model = DecisionTree::params() .max_depth(Some(3)) .fit(&train).unwrap(); }
- Creates a decision tree model with max depth of 3
- Trains the model on the current training fold
- Uses
unwrap()to handle potential errors (in production code, you'd want better error handling)
- Model Evaluation:
#![allow(unused)] fn main() { let accuracy = model.predict(&valid) .confusion_matrix(&valid) .unwrap() .accuracy(); }
- Makes predictions on the validation set
- Creates a confusion matrix comparing predictions to true labels
- Calculates the accuracy from the confusion matrix
- Collecting Results:
#![allow(unused)] fn main() { }).collect(); }
- Collects all 5 accuracy scores into a vector
- Each score represents the model's performance on a different validation fold
The key differences between this and the previous cross_validate_single method are:
- This is a more manual implementation
- It only evaluates one model configuration (max_depth=3)
- It gives you direct control over the training and evaluation process
- The results are collected into a simple vector of accuracy scores
This approach is useful when you want more control over the cross-validation process or when you need to implement custom evaluation metrics.