Binary Heap Implementation

About This Module

This module explores the binary heap data structure, which is the foundation of efficient priority queue implementations. We'll examine the binary heap's tree structure, array-based storage, and implement core operations like push and pop with O(log n) complexity.

Prework

Prework Reading

Read the following sections from "The Rust Programming Language" book:

Pre-lecture Reflections

Before class, consider these questions:

Why is the binary heap structure optimal for priority queue operations?
How does the complete binary tree property enable efficient array-based storage?
What are the key invariants that must be maintained in a max heap?
How do the parent-child index relationships work in array representation?
What are the trade-offs between binary heaps and other priority queue implementations?

Lecture

Learning Objectives

By the end of this module, you should be able to:

Understand the binary heap structure and its key properties
Navigate binary heap using array indices for parent and child nodes
Implement heapify operations to maintain heap ordering
Build push and pop operations with O(log n) complexity
Analyze the relationship between tree height and operation complexity
Compare custom implementations with Rust's standard library BinaryHeap

Popular implementation: binary heap

Binary heaps

Data organized into a binary tree (one root, each node with 0, 1 or 2 children)
Every internal node not smaller (or greater) than its children
Every layer is filled before the next layer starts

Basic property: The root has the current maximum (minimum), i.e., the answer to next pop

[picture of basic binary heap with heap ordering]

Heap storage properties

Efficient storage:

Tree levels filled from left to right
Can be mapped to a vector
Easy to move to the parent or children using vector indices

How are operations implemented?

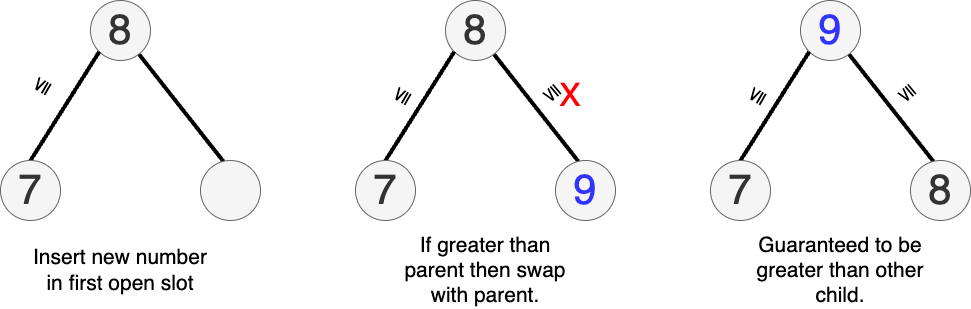
Push

add at the end the vector
fix the ordering by swapping with the parent if needed

Question: What is the maximum number of swaps you will have to do? Why?

$lo g_{2} (n)$

Pop

remove and return the root
replace with the last element
fix the ordering by comparing with children and swapping with each that is greater

Complexity of push and pop

Proportional to the number of levels
So $O (lo g n)$

Implementation

Utility methods

#![allow(unused)]
fn main() {
#[derive(Debug)]
struct MyBinaryHeap<T> {
    heap: Vec<T>,
    heap_size: usize,
}

impl<T> MyBinaryHeap<T> {
    fn new() -> MyBinaryHeap<T> {
        let heap: Vec<T> = vec![];
        let heap_size = 0;
        MyBinaryHeap { heap, heap_size }
    }

    // left child
    fn left(i: usize) -> usize {
        2 * i + 1
    }

    // right child of node i
    fn right(i: usize) -> usize {
        2 * i + 2
    }

    //parent of  node i
    fn parent(i: usize) -> usize {
        (i - 1) / 2  // integer divide
    }
}
}

Heapify -- Put everything in proper order

Make it so children are $\leq$ parents.

#![allow(unused)]
fn main() {
impl<T:PartialOrd+PartialEq+Copy> MyBinaryHeap<T> {
    fn heapify(&mut self, loc: usize) {
        let l = Self::left(loc);
        let r: usize = Self::right(loc);
        
        let mut largest = loc; // index of largest
        
        if l < self.heap_size && self.heap[l] > self.heap[largest] {
            largest = l;
        }
        if r < self.heap_size && self.heap[r] > self.heap[largest] {
            largest = r;
        }
        
        if largest != loc {
            // swap with child
            let tmp = self.heap[loc];
            self.heap[loc] = self.heap[largest];
            self.heap[largest] = tmp;
            
            self.heapify(largest);
        }
    }
}
}

Insert and Extract

#![allow(unused)]
fn main() {
impl<T:PartialOrd+PartialEq+Copy> MyBinaryHeap<T> {
    
    fn insert_val(&mut self, val: T) {
        self.heap_size += 1;
        self.heap.push(val);
        let mut i = self.heap_size - 1;

        // loop until we reach root and parent is less than current node
        while i != 0 && self.heap[Self::parent(i)] < self.heap[i] {

            // swap node with parent
            let tmp = self.heap[Self::parent(i)];
            self.heap[Self::parent(i)] = self.heap[i];
            self.heap[i] = tmp;

            // update node number
            i = Self::parent(i);  // Self is stand-in for data strucutre MyBinaryHeap
        }
    }
    
    fn extract_max(&mut self) -> Option<T> {
        if self.heap_size == 0 {
            return None;
        }
        
        if self.heap_size == 1 {
            self.heap_size -= 1;
            return Some(self.heap[0]);
        }
        
        let root = self.heap[0];
        self.heap[0] = self.heap[self.heap_size - 1]; // copy last element
        self.heap_size -= 1;
        self.heapify(0);
        return Some(root);
    }
}
}

Let's run the code

#![allow(unused)]
fn main() {
:dep rand="0.8.5"
use rand::Rng;

let mut h:MyBinaryHeap::<i32> = MyBinaryHeap::new();

// Generate 10 random numberrs between -1000 and 1000 and insert
for _i in 0..10 {
    let x = rand::thread_rng().gen_range(-1000..1000) as i32;
    h.insert_val(x);
}

println!("Print the BinaryHeap structure.");
println!("{:?}", h);

println!("\nExtract max values.");
let size = h.heap_size;
for _j in 0..size {
    let z = h.extract_max().unwrap();
    print!("{} ", z);
}

println!("\n\nPrint what's left of the BinaryHeap structure");
println!("{:?}", h);

}

Print the BinaryHeap structure.
MyBinaryHeap { heap: [983, 827, 654, 135, 757, -686, 191, -822, -349, 263], heap_size: 10 }

Extract max values.
983 827 757 654 263 191 135 -349 -686 -822 

Print what's left of the BinaryHeap structure
MyBinaryHeap { heap: [-822, -822, -686, -822, -349, -686, -822, -822, -349, 263], heap_size: 0 }

Note: the last debug print shouldn't display values with heap_size: 0.

What is the property of the list of values we extracted?

Or use the built in one from std::collections

#![allow(unused)]
fn main() {
use std::collections::BinaryHeap;

let mut heap = BinaryHeap::new();
heap.push(5);
heap.push(2);
heap.push(8);

while let Some(max) = heap.pop() {
    println!("{}", max);
}
// Outputs: 8, 5, 2
}

The values are extracted in sorted order (largest first)!

DS210 Course Notes